「シルドプロット」の版間の差分
細編集の要約なし |
|||
| (2人の利用者による、間の5版が非表示) | |||
| 1行目: | 1行目: | ||
英:Schild plot 又は Schild Regression 独:Schild-Plot 仏:Régression de Schild | 英:Schild plot 又は Schild Regression 独:Schild-Plot 仏:Régression de Schild | ||
同義語:シルド回帰、シルド解析 | 同義語:シルド回帰、シルド解析 | ||
シルドプロットとは、[[受容体]]に対する[[拮抗薬]](受容体遮断薬)の作用、特に[[競合的拮抗薬]]の作用の強さを求めるための解析手法である。薬理学者[[wikipedia:de:Heinz Otto Schild|Heinz Otto Schild]] (1906-1984)により提唱された手法で<ref><pubmed>9142394</pubmed></ref>、現在でも広く利用されている。 | シルドプロットとは、[[受容体]]に対する[[拮抗薬]](受容体遮断薬)の作用、特に[[競合的拮抗薬]]の作用の強さを求めるための解析手法である。薬理学者[[wikipedia:de:Heinz Otto Schild|Heinz Otto Schild]] (1906-1984)により提唱された手法で<ref><pubmed>9142394</pubmed></ref>、現在でも広く利用されている。 | ||
==プロットの方法 == | ==プロットの方法 == | ||
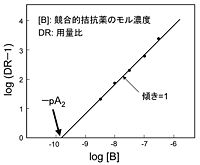
単一の受容体を介して発現する[[作動薬]]Aの作用の[[用量反応関係]]を、種々の濃度の拮抗薬Bの存在下で調べ、[[用量比]] DR (dose ratio) を求める。ここで DR とは、拮抗薬B存在下においてある一定の大きさの反応を引き起こす作動薬Aの[[wikipedia:ja:モル濃度|モル濃度]] [A] を、拮抗薬非存在下において同じ大きさの反応を引き起こすAのモル濃度 [A]<sub>0</sub> で割ったものである。横軸にBのモル濃度の[[wikipedia:ja:常用対数|常用対数]]、縦軸に(DR−1)の常用対数をとると、Bが競合的拮抗薬である場合は、傾きを1とする直線関係が得られる(図1)。このプロットから、競合的拮抗薬の作用強度の指標である pA<sub>2</sub> の値が求められる。[[Image:Schildplot.jpg|thumb|right| | 単一の受容体を介して発現する[[作動薬]]Aの作用の[[用量反応関係]]を、種々の濃度の拮抗薬Bの存在下で調べ、[[用量比]] DR (dose ratio) を求める。ここで DR とは、拮抗薬B存在下においてある一定の大きさの反応を引き起こす作動薬Aの[[wikipedia:ja:モル濃度|モル濃度]] [A] を、拮抗薬非存在下において同じ大きさの反応を引き起こすAのモル濃度 [A]<sub>0</sub> で割ったものである。横軸にBのモル濃度の[[wikipedia:ja:常用対数|常用対数]]、縦軸に(DR−1)の常用対数をとると、Bが競合的拮抗薬である場合は、傾きを1とする直線関係が得られる(図1)。このプロットから、競合的拮抗薬の作用強度の指標である pA<sub>2</sub> の値が求められる。[[Image:Schildplot.jpg|thumb|right|200px|図1 シルドプロットの1例]] | ||
== 競合的拮抗薬の場合 == | == 競合的拮抗薬の場合 == | ||
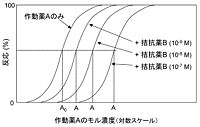
競合的拮抗薬は、受容体タンパク質内の同一の部位に対する可逆的な結合に関して作動薬と競合する分子である。ある組織/細胞において、作動薬Aが単一の受容体を介して反応を引き起こす場合、Aの濃度の対数 log [A] を横軸、組織/細胞の最大反応に対する反応の百分率を縦軸にとると、[[wikipedia:ja:シグモイド|シグモイド]]型の[[用量反応曲線]]が得られる。次に、一定濃度の競合的拮抗薬Bの存在下で同様にAの用量反応関係を求めると、その曲線は拮抗薬非存在下で求めた曲線と比べて高用量側(右側)にシフトする。Bの濃度 [B] が高いほど、Aの用量反応曲線のシフトの幅([A]/[A]<sub>0</sub>、すなわちDR)も大きくなる(図2)。 [[Image:Doseresponse.jpg|thumb|right| | 競合的拮抗薬は、受容体タンパク質内の同一の部位に対する可逆的な結合に関して作動薬と競合する分子である。ある組織/細胞において、作動薬Aが単一の受容体を介して反応を引き起こす場合、Aの濃度の対数 log [A] を横軸、組織/細胞の最大反応に対する反応の百分率を縦軸にとると、[[wikipedia:ja:シグモイド|シグモイド]]型の[[用量反応曲線]]が得られる。次に、一定濃度の競合的拮抗薬Bの存在下で同様にAの用量反応関係を求めると、その曲線は拮抗薬非存在下で求めた曲線と比べて高用量側(右側)にシフトする。Bの濃度 [B] が高いほど、Aの用量反応曲線のシフトの幅([A]/[A]<sub>0</sub>、すなわちDR)も大きくなる(図2)。 [[Image:Doseresponse.jpg|thumb|right|200px|図2 種々の濃度の拮抗薬Bの存在下での作動薬Aの用量反応曲線]] | ||
DRと[B]との間には、以下の関係が成り立つ。 | DRと[B]との間には、以下の関係が成り立つ。 | ||
| 67行目: | 58行目: | ||
・拮抗薬の受容体への結合が不可逆的である場合 | ・拮抗薬の受容体への結合が不可逆的である場合 | ||
・[[リガンド]](作動薬および拮抗薬)の受容体への結合が[[協同性]]を示す場合 | |||
・リガンド親和性の異なる複数の受容体サブタイプが発現している場合<ref><pubmed>17079019</pubmed></ref> | ・リガンド親和性の異なる複数の受容体サブタイプが発現している場合<ref><pubmed>17079019</pubmed></ref> | ||
| 77行目: | 68行目: | ||
<references /> | <references /> | ||
(執筆者:香月博志、担当編集委員:林 康紀) | |||
2012年1月24日 (火) 01:08時点における版
英:Schild plot 又は Schild Regression 独:Schild-Plot 仏:Régression de Schild
同義語:シルド回帰、シルド解析
シルドプロットとは、受容体に対する拮抗薬(受容体遮断薬)の作用、特に競合的拮抗薬の作用の強さを求めるための解析手法である。薬理学者Heinz Otto Schild (1906-1984)により提唱された手法で[1]、現在でも広く利用されている。
プロットの方法
単一の受容体を介して発現する作動薬Aの作用の用量反応関係を、種々の濃度の拮抗薬Bの存在下で調べ、用量比 DR (dose ratio) を求める。ここで DR とは、拮抗薬B存在下においてある一定の大きさの反応を引き起こす作動薬Aのモル濃度 [A] を、拮抗薬非存在下において同じ大きさの反応を引き起こすAのモル濃度 [A]0 で割ったものである。横軸にBのモル濃度の常用対数、縦軸に(DR−1)の常用対数をとると、Bが競合的拮抗薬である場合は、傾きを1とする直線関係が得られる(図1)。このプロットから、競合的拮抗薬の作用強度の指標である pA2 の値が求められる。
競合的拮抗薬の場合
競合的拮抗薬は、受容体タンパク質内の同一の部位に対する可逆的な結合に関して作動薬と競合する分子である。ある組織/細胞において、作動薬Aが単一の受容体を介して反応を引き起こす場合、Aの濃度の対数 log [A] を横軸、組織/細胞の最大反応に対する反応の百分率を縦軸にとると、シグモイド型の用量反応曲線が得られる。次に、一定濃度の競合的拮抗薬Bの存在下で同様にAの用量反応関係を求めると、その曲線は拮抗薬非存在下で求めた曲線と比べて高用量側(右側)にシフトする。Bの濃度 [B] が高いほど、Aの用量反応曲線のシフトの幅([A]/[A]0、すなわちDR)も大きくなる(図2)。
DRと[B]との間には、以下の関係が成り立つ。
DR−1 = [B]/KB ・・・・・(1)
式(1)は、以下の条件に基づいて立てた連立方程式より導かれる [2]。
a) 作動薬Aは、受容体に可逆的に結合し、その解離定数は KD である。
b) 競合的拮抗薬Bは、受容体に可逆的に結合し、その解離定数は KB である。
c) 「受容体総数」=「リガンドの結合していない受容体」+「Aの結合した受容体」+「Bの結合した受容体」
なお a)および b)は、酵素反応速度論におけるミカエリス・メンテンの仮定(酵素と基質とが可逆的に結合し、複合体を形成する)と同様である。
式(1)の両辺の対数をとると
log (DR−1) = log [B] − log KB ・・・・・(2)
したがって、log [B] とlog (DR−1) は直線関係となる。
pA2
競合的拮抗薬の作用強度を表す指標として pA2 が用いられる。pA2 は「作動薬単独時の用量反応曲線を2倍だけ高用量側にシフトさせるのに必要な競合的拮抗薬のモル濃度の負対数」と定義される。この時の競合的拮抗薬Bのモル濃度を [B2] とすると、pA2 の定義は式(3)のように表される。
pA2 = −log [B2] ・・・・・(3)
さらにこの時 DR = 2 であるから、式(2)より log [B2] = log KB となり、式(3)と合わせて
pA2 = −log KB ・・・・・(4)
となる。すなわち pA2 は、受容体に対する競合的拮抗薬Bの解離定数 KB を直接反映する指標である。
また、式(4)を式(2)に代入すると
log (DR−1) = log [B] + pA2
となる。したがって、シルドプロットの横軸切片からpA2が求められる(図1)。
理論から外れる場合
シルドプロットを作成した結果、傾きを1とする直線が得られない場合は、解析の前提となる条件が成立していないものと判断される。主な要因としては以下のことが考えられる。
・受容体タンパク質上の拮抗薬の結合部位が、作動薬の結合部位と異なる場合(=アロステリック結合部位に結合して作用する非拮抗阻害作用)
・拮抗薬の受容体への結合が不可逆的である場合
・リガンド(作動薬および拮抗薬)の受容体への結合が協同性を示す場合
・リガンド親和性の異なる複数の受容体サブタイプが発現している場合[3]
・測定条件下においてリガンド-受容体結合が平衡に達していなかった場合(組織/細胞がリガンドの取込み機構を有している場合など)
参考文献
- ↑
Schild, H.O. (1997).
pA, a new scale for the measurement of drug antagonism. 1947. British journal of pharmacology, 120(4 Suppl), 29-46; discussion 27-8. [PubMed:9142394] [PMC] [WorldCat] [DOI] - ↑ 田中千賀子・加藤隆一編
NEW薬理学 改訂第6版(南江堂)2011, p. 11 - ↑
Tallarida, R.J. (2007).
Interactions between drugs and occupied receptors. Pharmacology & therapeutics, 113(1), 197-209. [PubMed:17079019] [PMC] [WorldCat] [DOI]
(執筆者:香月博志、担当編集委員:林 康紀)