「量子仮説」の版間の差分
細編集の要約なし |
細編集の要約なし |
||
| (3人の利用者による、間の10版が非表示) | |||
| 1行目: | 1行目: | ||
<div align="right"> | |||
<font size="+1">[http://researchmap.jp/read0069999 川口 真也]、[http://researchmap.jp/7000002629 坂場 武史]</font><br> | |||
''同志社大学''<br> | |||
DOI:<selfdoi /> 原稿受付日:2012年9月13日 原稿完成日:2012年10月3日<br> | |||
担当編集委員:[http://researchmap.jp/michisukeyuzaki 柚崎 通介](慶應義塾大学 医学部生理学)<br> | |||
</div> | |||
[[Image:Katz.png|thumb|right|350px|'''図.低Ca液中で記録されたEPPの振幅分布とmEPP'''<br>カエル神経筋接合部で、アセチルコリン放出を低くした状態で記録されたEPPの振幅と、その観察回数を示している。ヒストグラムのピークが、mEPPの振幅の整数倍となることが分かる。マゼンタの実線はポアソン分布から予測されるEPP振幅の分布を表している。<br>del Castillo,Katz<ref name=ref2><pubmed> 13175199 </pubmed></ref>より改変]] | [[Image:Katz.png|thumb|right|350px|'''図.低Ca液中で記録されたEPPの振幅分布とmEPP'''<br>カエル神経筋接合部で、アセチルコリン放出を低くした状態で記録されたEPPの振幅と、その観察回数を示している。ヒストグラムのピークが、mEPPの振幅の整数倍となることが分かる。マゼンタの実線はポアソン分布から予測されるEPP振幅の分布を表している。<br>del Castillo,Katz<ref name=ref2><pubmed> 13175199 </pubmed></ref>より改変]] | ||
英:quantal hypothesis 独:Quantenhypothese 仏:hypothèse des quanta | 英:quantal hypothesis 独:Quantenhypothese 仏:hypothèse des quanta | ||
同義語:量子説、素量説 | 同義語:量子説、素量説 | ||
{{box|text= Katzらが提唱した神経細胞の情報伝達に関する仮説である。神経筋接合部直下で、神経線維を刺激しないときにも、自発的に一定の脱分極が不規則に起こることを見出し、これを微小終板電位(mEPP)と呼んだ。これが神経伝達物質が神経終末からまとまった単位量で自発的に放出されることにより引き起こされると考え、その単位量を量子と呼んだ。さらに神経刺激により誘発された終板電位の振幅の分布がポアソン分布でよく説明できることから、神経終末にmEPPを引き起こす単一量子が多数存在し、活動電位に応じて個々の量子が確率的にランダムに放出されるという量子仮説に至った。現在では、個々の量子は一個のシナプス顆粒に相当することが判っている。}} | |||
量子仮説は、1950年代に[[ | 量子仮説は、1950年代に[[wj:ベルンハルト・カッツ|Bernard Katz]]らが提唱した神経細胞の情報伝達に関する仮説であり、神経系の[[情報伝達]]が離散的性質(量子性)をもつことを提唱した<ref>'''クフラー、ニコルス、マーチン''' <br> ニューロンから脳へ 神経生物学入門 第2版<br> ''廣川書店'':1988 </ref> | ||
。 | 。 | ||
[[神経筋標本]]の筋細胞で[[活動電位]]が起こらないように薬理学的操作を加えた条件下では、[[神経線維]]を刺激したときに筋細胞において[[終板電位]](endplate potential: EPP)が観察される。1952年に、[[w:Paul_Fatt|Fatt]]とKatzは[[wj:カエル|カエル]]の[[神経筋接合部]]直下では、神経線維を刺激しないときにも、自発的に1 mV程度の大きさをもつ[[脱分極]]が不規則に起こることを見出し、これを[[微小終板電位]](mEPP)と呼んだ<ref><pubmed> 14946732 </pubmed></ref>。mEPPはEPPと似た時間経過をとる。したがって、Katzらは[[アセチルコリン]]が[[神経終末]]からまとまった単位量で自発的に放出されることにより、mEPPが引き起こされると考え、その単位量を量子(quantum)と呼んだ。現在では、神経終末に存在する[[神経伝達物質]]が充填された(例えばアセチル[[コリン]]の場合約10000分子)直径30-50ナノメートルほどの[[シナプス小胞]]が、自発的に[[細胞膜]]と融合して内部のアセチルコリンが[[開口放出]]されたときに生じる反応がmEPPであると考えられている。 | |||
del CastilloとKatzらは、細胞外の[[カルシウム]]濃度を低下、[[ | del CastilloとKatzらは、細胞外の[[カルシウム]]濃度を低下、[[wj:マグネシウム|マグネシウム]]濃度を上昇させることにより伝達物質放出の確率を低下させた条件下で、神経刺激により誘発されたEPPの大きさの変動を統計的に解析した<ref name=ref2 />。EPPが全く発生しない場合や、最小振幅の整数倍の大きさで振幅が段階的に変動したEPPが確率的に記録されるが、これらのEPPの記録回数を振幅に対してプロットすると、[[wj:ポアソン分布|ポアソン分布]]とよく一致する(図)。 また、その最小振幅の大きさは、mEPPの大きさとほぼ同じ大きさとなることも分かった。振幅の分布がポアソン分布でよく説明できることから、神経終末にmEPPを引き起こす単一量子([[シナプス小胞]])が多数存在し、[[活動電位]]の発生に応じて個々の量子が確率的にランダムに放出されるという仮説に至った。これを量子仮説と呼ぶ。 | ||
このような実験は、伝達物質放出の確率を低くした条件でなされたため、EPPの振幅とその観察頻度はポアソン分布と一致するが、生理的な条件下ではより放出確率が高いため、一回の活動電位で放出される量子数は数百個になると考えられ、[[ | このような実験は、伝達物質放出の確率を低くした条件でなされたため、EPPの振幅とその観察頻度はポアソン分布と一致するが、生理的な条件下ではより放出確率が高いため、一回の活動電位で放出される量子数は数百個になると考えられ、[[wj:二項分布|二項分布]]に従う。なお、数学的には、二項分布は特別な条件下(ここでは放出確率が低い)において、ポアソン分布と一致する。 Katzらが行った一連の解析から、[[シナプス前終末]]における独立した放出部位がn箇所、活動電位が起こった時の個々の放出部位での[[放出確率]]がp、1量子に対する[[シナプス後部]]での反応の大きさをqとすると、一回の活動電位に対するシナプス応答の大きさの平均値mは、 | ||
:<math>\ m = npq\, </math> | :<math>\ m = npq\, </math> | ||
と考えることができ、これら3つの変数がシナプス伝達効率を規定すると考えることが出来る。それぞれの値を導出するにはさまざまな方法が考えられ総じて[[素量解析]]とよばれているが、たとえばSilverらはシナプス応答の平均と分散から導出する方法を考案している<ref><pubmed> 9660900 </pubmed></ref>。ただし、伝達物質の放出量が多い状況では、シナプス後部の伝達物質[[受容体]]が飽和するため、伝達物質の放出量に比例してシナプス後部が応答することが出来ず、実際のシナプス応答の平均値mは上式で計算するよりも小さくなるので注意を要する。特に中枢神経系においては、[[シナプス前]]終末における伝達物質放出部位の個数と、アクティブゾーンと呼ばれる小胞の膜融合に必要な分子群が集積した部位の個数が一致しているかどうかは議論の余地がある。たとえば、単一の神経終末から非独立的に複数の小胞が放出されることがあり(multivescicular release)、その場合シナプス後部の受容体が飽和される可能性が高くなる。また、個々の放出部位が独立している場合であっても、シナプス後部の受容体を共有している場合には、同時に複数の小胞が独立に放出されるという、量子仮説の仮定が満たされなくなるため、上式でのシナプス応答の推定が合致しない場合もある<ref><pubmed> 7507341 </pubmed></ref>。 | |||
こうしたシナプス小胞を介した量子的な神経伝達物質放出は、神経筋接合部だけでなく神経細胞間シナプスにおいても起こり、[[グルタミン酸]]や[[GABA]]、[[モノアミン]]および[[ペプチド]]などの多くの神経伝達物質が量子的に放出される。また、神経細胞間シナプスにおいても、自発的なシナプス小胞の放出が観察されている。しかしながら、シナプス小胞の開口放出が自発的に起こる仕組みは未だに分かっておらず、また自発的に放出されるシナプス小胞が、活動電位発生に応じて放出されるシナプス小胞と同一のものであるのか、あるいは別種のものであるのかについても論争中である。 | |||
物理学分野においては、1900年に[[ | 物理学分野においては、1900年に[[wj:マックス・プランク|Max Planck]]が提唱した[[wj:光|光]]の[[wj:エネルギー|エネルギー]]にみられる量子性に関する概念を[[wj:量子仮説|量子仮説]]と呼び、後に大きく発展した量子論の基礎として頻繁に用いられるため、注意を要する。 | ||
==関連項目== | ==関連項目== | ||
| 42行目: | 51行目: | ||
==参考文献== | ==参考文献== | ||
<references /> | <references /> | ||
2020年9月12日 (土) 18:30時点における最新版
川口 真也、坂場 武史
同志社大学
DOI:10.14931/bsd.2481 原稿受付日:2012年9月13日 原稿完成日:2012年10月3日
担当編集委員:柚崎 通介(慶應義塾大学 医学部生理学)
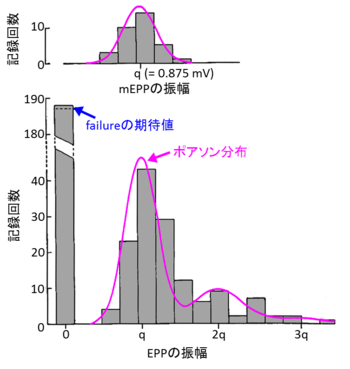
カエル神経筋接合部で、アセチルコリン放出を低くした状態で記録されたEPPの振幅と、その観察回数を示している。ヒストグラムのピークが、mEPPの振幅の整数倍となることが分かる。マゼンタの実線はポアソン分布から予測されるEPP振幅の分布を表している。
del Castillo,Katz[1]より改変
英:quantal hypothesis 独:Quantenhypothese 仏:hypothèse des quanta
同義語:量子説、素量説
Katzらが提唱した神経細胞の情報伝達に関する仮説である。神経筋接合部直下で、神経線維を刺激しないときにも、自発的に一定の脱分極が不規則に起こることを見出し、これを微小終板電位(mEPP)と呼んだ。これが神経伝達物質が神経終末からまとまった単位量で自発的に放出されることにより引き起こされると考え、その単位量を量子と呼んだ。さらに神経刺激により誘発された終板電位の振幅の分布がポアソン分布でよく説明できることから、神経終末にmEPPを引き起こす単一量子が多数存在し、活動電位に応じて個々の量子が確率的にランダムに放出されるという量子仮説に至った。現在では、個々の量子は一個のシナプス顆粒に相当することが判っている。
量子仮説は、1950年代にBernard Katzらが提唱した神経細胞の情報伝達に関する仮説であり、神経系の情報伝達が離散的性質(量子性)をもつことを提唱した[2] 。
神経筋標本の筋細胞で活動電位が起こらないように薬理学的操作を加えた条件下では、神経線維を刺激したときに筋細胞において終板電位(endplate potential: EPP)が観察される。1952年に、FattとKatzはカエルの神経筋接合部直下では、神経線維を刺激しないときにも、自発的に1 mV程度の大きさをもつ脱分極が不規則に起こることを見出し、これを微小終板電位(mEPP)と呼んだ[3]。mEPPはEPPと似た時間経過をとる。したがって、Katzらはアセチルコリンが神経終末からまとまった単位量で自発的に放出されることにより、mEPPが引き起こされると考え、その単位量を量子(quantum)と呼んだ。現在では、神経終末に存在する神経伝達物質が充填された(例えばアセチルコリンの場合約10000分子)直径30-50ナノメートルほどのシナプス小胞が、自発的に細胞膜と融合して内部のアセチルコリンが開口放出されたときに生じる反応がmEPPであると考えられている。
del CastilloとKatzらは、細胞外のカルシウム濃度を低下、マグネシウム濃度を上昇させることにより伝達物質放出の確率を低下させた条件下で、神経刺激により誘発されたEPPの大きさの変動を統計的に解析した[1]。EPPが全く発生しない場合や、最小振幅の整数倍の大きさで振幅が段階的に変動したEPPが確率的に記録されるが、これらのEPPの記録回数を振幅に対してプロットすると、ポアソン分布とよく一致する(図)。 また、その最小振幅の大きさは、mEPPの大きさとほぼ同じ大きさとなることも分かった。振幅の分布がポアソン分布でよく説明できることから、神経終末にmEPPを引き起こす単一量子(シナプス小胞)が多数存在し、活動電位の発生に応じて個々の量子が確率的にランダムに放出されるという仮説に至った。これを量子仮説と呼ぶ。
このような実験は、伝達物質放出の確率を低くした条件でなされたため、EPPの振幅とその観察頻度はポアソン分布と一致するが、生理的な条件下ではより放出確率が高いため、一回の活動電位で放出される量子数は数百個になると考えられ、二項分布に従う。なお、数学的には、二項分布は特別な条件下(ここでは放出確率が低い)において、ポアソン分布と一致する。 Katzらが行った一連の解析から、シナプス前終末における独立した放出部位がn箇所、活動電位が起こった時の個々の放出部位での放出確率がp、1量子に対するシナプス後部での反応の大きさをqとすると、一回の活動電位に対するシナプス応答の大きさの平均値mは、
と考えることができ、これら3つの変数がシナプス伝達効率を規定すると考えることが出来る。それぞれの値を導出するにはさまざまな方法が考えられ総じて素量解析とよばれているが、たとえばSilverらはシナプス応答の平均と分散から導出する方法を考案している[4]。ただし、伝達物質の放出量が多い状況では、シナプス後部の伝達物質受容体が飽和するため、伝達物質の放出量に比例してシナプス後部が応答することが出来ず、実際のシナプス応答の平均値mは上式で計算するよりも小さくなるので注意を要する。特に中枢神経系においては、シナプス前終末における伝達物質放出部位の個数と、アクティブゾーンと呼ばれる小胞の膜融合に必要な分子群が集積した部位の個数が一致しているかどうかは議論の余地がある。たとえば、単一の神経終末から非独立的に複数の小胞が放出されることがあり(multivescicular release)、その場合シナプス後部の受容体が飽和される可能性が高くなる。また、個々の放出部位が独立している場合であっても、シナプス後部の受容体を共有している場合には、同時に複数の小胞が独立に放出されるという、量子仮説の仮定が満たされなくなるため、上式でのシナプス応答の推定が合致しない場合もある[5]。
こうしたシナプス小胞を介した量子的な神経伝達物質放出は、神経筋接合部だけでなく神経細胞間シナプスにおいても起こり、グルタミン酸やGABA、モノアミンおよびペプチドなどの多くの神経伝達物質が量子的に放出される。また、神経細胞間シナプスにおいても、自発的なシナプス小胞の放出が観察されている。しかしながら、シナプス小胞の開口放出が自発的に起こる仕組みは未だに分かっておらず、また自発的に放出されるシナプス小胞が、活動電位発生に応じて放出されるシナプス小胞と同一のものであるのか、あるいは別種のものであるのかについても論争中である。
物理学分野においては、1900年にMax Planckが提唱した光のエネルギーにみられる量子性に関する概念を量子仮説と呼び、後に大きく発展した量子論の基礎として頻繁に用いられるため、注意を要する。
関連項目
- アクティブゾーン
- アセチルコリン
- エクソサイトーシス
- カルシウム
- カルシウムチャネル
- カルシウムドメイン
- シナプス
- シナプス小胞
- シナプス前終末
- 神経筋接合部
- 神経伝達物質
- 分泌小胞
- 放出可能プール
- 放出確率
- 膜融合
参考文献
- ↑ 1.0 1.1
DEL CASTILLO, J., & KATZ, B. (1954).
Quantal components of the end-plate potential. The Journal of physiology, 124(3), 560-73. [PubMed:13175199] [PMC] [WorldCat] [DOI] - ↑ クフラー、ニコルス、マーチン
ニューロンから脳へ 神経生物学入門 第2版
廣川書店:1988 - ↑
FATT, P., & KATZ, B. (1952).
Spontaneous subthreshold activity at motor nerve endings. The Journal of physiology, 117(1), 109-28. [PubMed:14946732] [PMC] [WorldCat] - ↑
Silver, R.A., Momiyama, A., & Cull-Candy, S.G. (1998).
Locus of frequency-dependent depression identified with multiple-probability fluctuation analysis at rat climbing fibre-Purkinje cell synapses. The Journal of physiology, 510 ( Pt 3), 881-902. [PubMed:9660900] [PMC] [WorldCat] [DOI] - ↑
Tong, G., & Jahr, C.E. (1994).
Multivesicular release from excitatory synapses of cultured hippocampal neurons. Neuron, 12(1), 51-9. [PubMed:7507341] [WorldCat] [DOI]
