「相互相関解析」の版間の差分

提供：脳科学辞典
ナビゲーションに移動 検索に移動
細編集の要約なし
(3人の利用者による、間の13版が非表示)
1行目: 1行目:
<div align="right"> 
<font size="+1">[http://researchmap.jp/shiozaki 塩崎 博史]</font><br>
''独立行政法人理化学研究所 脳科学総合研究センター''<br>
DOI：<selfdoi />　原稿受付日：2012年5月14日　原稿完成日：2012年8月16日<br>
担当編集委員：[http://researchmap.jp/ichirofujita 藤田 一郎]（大阪大学 大学院生命機能研究科）<br>
</div>
英語名：cross-correlation analysis
英語名：cross-correlation analysis


{{box|text=
　相互相関解析とは、二つの時系列信号の類似度を、相互相関関数を用いて評価する方法である。神経科学の分野においては、主に細胞間の機能的結合を推定する目的で、同時計測した二つの神経細胞の活動に対して相互相関解析が行われる。
　相互相関解析とは、二つの時系列信号の類似度を評価することで、信号間の関係（同期している、片方が遅れている、無関係である等）を検討する方法である。類似度の評価に[[wikipedia:ja:相互相関関数|相互相関関数]]を用いることから、その名がついた。神経科学の分野においては、主に細胞間の機能的結合を推定する目的で、同時計測した二つの[[神経細胞]]の活動に対して相互相関解析が行われる。
}}


==解析方法==
==解析方法==
　相互相関関数の定義は学問分野、研究者によって異なる。ここでは神経科学の分野でしばしば用いられる定義について述べる。
　相互相関関数の定義は学問分野、研究者によって異なる。ここでは神経科学の分野でしばしば用いられる定義について述べる。


[[Image:CCG_Fig1.png|thumb|350px|'''図１．相互相関関数の例'''<br>二つの仮想的な細胞のスパイク活動から計算した相互相関関数。平均10ヘルツで活動電位を発射する二つの細胞から5分間にわたり同時に活動を計測する実験をシミュレートし、相互相関関数を求めた。あるビンにおいて細胞が発火している状態を <math>X(t) = 1</math> で、発火していない状態を <math>X(t) = 0</math> で表し、計算を行った。'''A、'''二つの細胞が同期して活動する傾向がある場合、相互相関関数は時間差0にピークを持つ。'''B、'''2つの細胞の活動の間に何の関係性もない場合、相互相関関数は平坦となる]]  
[[Image:CCG_Fig1.png|thumb|400px|'''図１ 相互相関関数の例'''<br>２つの仮想的な細胞のスパイク活動から計算した相互相関関数。平均10ヘルツで活動電位を発射する２つの細胞から5分間にわたり同時に活動を計測する実験をシミュレートし、相互相関関数を求めた。あるビンにおいて細胞が発火している状態を <math>X(t) = 1</math> で、発火していない状態を <math>X(t) = 0</math> で表した。'''A、'''２つの細胞が同期して活動する傾向がある場合、相互相関関数は時間差0にピークを持つ。'''B、'''２つの細胞の活動の間に何の関係性もない場合、相互相関関数は平坦となる]]  


　ある二つの神経細胞の活動（例えば[[活動電位]]の発生タイミング）を同時に計測したとする。計測期間を <math> T </math> 個のビンに区切り、 <math>t</math> 番目のビンにおけるある細胞の活動を <math>X(t)</math> で、もう一つの細胞の活動を <math>Y(t)</math> で表す。このとき <math>X(t)</math> と <math>Y(t)</math> の相互相関関数（相互相関ヒストグラム） <math>C_{XY}(\tau)</math> は、次のように定義される。
　ある二つの神経細胞の活動（例えば活動電位の発生タイミング）を同時に計測したとする。計測期間を <math> T </math> 個のビンに区切り、 <math>t</math> 番目のビンにおけるある細胞の活動を <math>X(t)</math> で、もう一つの細胞の活動を <math>Y(t)</math> で表す。このとき <math>X(t)</math> と <math>Y(t)</math> の相互相関関数（相互相関ヒストグラム） <math>C_{XY}(\tau)</math> は、次のように定義される。
:<math>C_{XY}(\tau) = \sum_{t = 1}^{T} X(t)\ Y(t+\tau),</math>
:<math>C_{XY}(\tau) = \sum_{t = 1}^{T} X(t)\ Y(t+\tau),</math>


ここで <math>\tau</math> は <math> X </math> と <math> Y </math> の間の時間差（time-lag）を表す。相互相関関数は、細胞 <math> X </math> の活動と細胞 <math> Y </math> の活動との時間的関係性を反映する（図1）。
ここで <math>\tau</math> は <math> X </math> と <math> Y </math> の間の時間差（time-lag）を表す。相互相関関数は、細胞 <math> X </math> の活動と細胞 <math> Y </math> の活動との関係性を反映する（図１）。
 
[[Image:CCG_Fig2.png|thumb|350px|'''図2．相互共分散関数の例'''<br>二つの仮想的な細胞のスパイク活動から計算した相互共分散関数（青線）。相互相関関数（黒線）には、細胞活動間の共分散（相関）に由来する成分と、平均発火率の変化に由来する成分が含まれる。細胞活動が独立である場合に期待される相互相関関数（赤線）を差し引くことで、共分散に由来する成分を抽出することができる。この例では、二つの細胞の活動の間に正の相関がある。]]


　神経活動はしばしば[[wikipedia:ja:確率過程|確率過程]]としてモデル化される。この場合、相互相関関数の値は複数の統計量（細胞活動の[[wikipedia:ja:平均|平均]]や[[wikipedia:ja:共分散|共分散]]）を反映する。例えば、二つの細胞の活動が独立、つまり共分散が0であっても、両細胞の活動の平均が時間的に同じように変化すると、相互相関関数は時間差0で最大となる場合がある。実験データから計算した相互相関関数と、二つの細胞の活動が独立である場合に期待される相互相関関数（[[wikipedia:ja:帰無仮説|帰無仮説]]）の差を取ることで、（いくつかの仮定のもとに）二つの細胞の活動が独立かどうかを統計的に検討することができる<ref name=perkel><pubmed> 4292792 </pubmed></ref>。この差は[[wikipedia:ja:相互共分散関数|相互共分散関数]] <math>Cov_{XY}(\tau)</math> と呼ばれる。
　神経活動はしばしば確率過程としてモデル化される。この場合、相互相関関数の値は複数の統計量（細胞活動の平均や共分散）を反映する。例えば、二つの細胞の活動が独立、つまり共分散が0であっても、両細胞の活動の平均が時間的に同じように変化すると、相互相関関数は時間差0で最大となる場合がある（図２）。実験データから計算した相互相関関数と、二つの細胞の活動が独立である場合に期待される相互相関関数（帰無仮説）の差を取ることで、二つの細胞の活動が独立かどうかを統計的に検討することができる<ref name=perkel><pubmed> 4292792 </pubmed></ref>。この差は相互共分散関数 <math>Cov_{XY}(\tau)</math> と呼ばれる。
:<math>Cov_{XY}(\tau) = \sum_{t = 1}^{T} \bigl\{X(t)Y(t+\tau)-{\mu}_X(t){\mu}_Y(t+\tau)\bigr\} ,</math>
:<math>Cov_{XY}(\tau) = \sum_{t = 1}^{T} \bigl\{X(t)Y(t+\tau)-{\mu}_X(t){\mu}_Y(t+\tau)\bigr\} ,</math>


ここで <math>{\mu}_X(t)</math> と <math>{\mu}_Y(t)</math> は <math>t</math> 番目のビンにおける細胞 <math>X</math> と細胞 <math>Y</math> の活動の平均を表す。相互共分散関数は、細胞 <math> X </math> の活動と細胞 <math> Y </math> の活動の間の相関（共分散）の度合いを表す（図２）。関数 <math>Cov_{XY}(\tau)</math> のことを相互相関関数と呼ぶ場合もあるので、注意が必要である。細胞活動の平均の変化が感覚入力によって引き起こされている場合、細胞活動の平均の[[wikipedia:ja:積|積]]（帰無仮説）を[[wikipedia:ja:信号相関|信号相関]]、相互共分散関数を[[wikipedia:ja:ノイズ相関|ノイズ相関]]と呼ぶ。なお、上のように定義した相互共分散関数の値は計測時間や平均活動度の違いによって変化する。異なる実験間で結果を比較するために、相互共分散関数を総[[スパイク]]数、細胞活動の平均、分散等で割ることで[[正規化]]する場合がある<ref><pubmed> 11222658 </pubmed></ref>。
ここで <math>{\mu}_X(t)</math> と <math>{\mu}_Y(t)</math> は <math>t</math> 番目のビンにおける細胞 <math>X</math> と細胞 <math>Y</math> の活動の平均を表す。関数 <math>Cov_{XY}(\tau)</math> のことを相互相関関数と呼ぶ場合もあるので、注意が必要である。上のように定義した相互共分散関数の値は計測時間や平均活動度の違いによって変化する。異なる実験間で結果を比較するために、相互共分散関数の正規化が行われる場合がある<ref><pubmed> 11222658 </pubmed></ref>。


　実際の実験においては、細胞活動の平均 <math>{\mu}_X(t)</math> 、 <math>{\mu}_Y(t)</math> は未知であるので、帰無仮説は計測した細胞活動をもとに設定しなければならない<ref name=perkel />。帰無仮説の設定は、同じ[[感覚]]刺激を繰り返し与えることで得た細胞活動データを用いて行う。通常、片方の細胞活動データの試行番号をランダムに並べ替えたり、試行番号を１つずらすことで、細胞活動が独立であった場合に得られるであろう相互相関関数を計算する。前者の帰無仮説設定法により得た相互共分散関数を[[シャッフル補正相互相関ヒストグラム]]（shuffle-corrected cross-correlogram）、後者の方法により得た相互共分散関数を[[シフト補正相互相関ヒストグラム]]（shift-corrected cross-correlogram）と呼ぶ。なお、スパイク活動の相関の有意性検定については、上記以外にも数多くの帰無仮説設定方法が考案されている<ref><pubmed> 19129298 </pubmed></ref>。
　
　
　スパイク活動の相関の有意性検定については、上記方法以外にも数多くの帰無仮説設定方法が考案されている<ref><pubmed> 19129298 </pubmed></ref>。  


　相互相関解析はスパイク活動の他、[[膜電位]]、[[膜電流]]、[[カルシウム]]応答などに適用されている。
　なお


==解釈==
==解釈==
　相互共分散関数の形状から、神経回路の機能的結合関係を推定することができると考えられている。例えば、ある二つの細胞の活動から計算した相互共分散関数が時間差0に幅の狭い大きなピークを持つ場合、二つの細胞は共通の興奮性入力を受け取っていると考えられる<ref><pubmed> 1000297 </pubmed></ref><ref name=toyama><pubmed> 6267211 </pubmed></ref>。また、相互共分散関数のピークの位置、幅を分析することにより、細胞間の興奮性結合や抑制性結合を推定することも可能である<ref name=perkel /><ref name=toyama /><ref><pubmed> 14711977 </pubmed></ref>。


　相互共分散関数の形状から、神経回路の[[機能的結合]]関係を推定することができると考えられている<ref name=perkel /><ref name=ostojic><pubmed> 19692598 </pubmed></ref>。例えば、ある二つの細胞の活動から計算した相互共分散関数が時間差0に幅の狭い大きなピークを持つ場合（図2）、二つの細胞は共通の興奮性入力を受け取っていると考えられる<ref><pubmed> 1000297 </pubmed></ref><ref name=toyama><pubmed> 6267211 </pubmed></ref>。相互共分散関数のピークの位置、幅を分析することにより、細胞間の興奮性結合や抑制性結合を推定することも可能である<ref name=perkel /><ref name=toyama /><ref><pubmed> 14711977 </pubmed></ref>。細胞 <math>X</math> から細胞 <math>Y</math> への興奮性結合の強度を定量化するために、細胞 <math>X</math> のスパイクの後どのくらいの割合で細胞 <math>Y</math> がスパイクを発射したか（efficacy）や、細胞 <math>Y</math> が発射したスパイクのうちどのくらいの割合が細胞 <math>X</math> のスパイクの後に発生したか（contribution）といった指標が用いられる<ref><pubmed> 5028229 </pubmed></ref>。
　相互相関解析は機能的結合を間接的に推定する方法であるため、結果の解釈には曖昧性が残る可能性が指摘されている。例えば、異なるメカニズムで働く神経回路から、同じようなピーク位置、幅を持つ相互相関関数が得られる場合がある<ref name=perkel /><ref><pubmed> 10490937 </pubmed></ref>。また、共通入力を受け取っていても、相互相関関数にピークが見られない場合もある<ref><pubmed> 20110507 </pubmed></ref>。
==関連項目==
同義語：覚醒中枢（脳幹網様体の解説で）


　相互相関解析は機能的結合を間接的に推定する方法であるため、結果の解釈には曖昧性が残る可能性が指摘されている<ref name=perkel /><ref name=ostojic /><ref name=brody><pubmed> 10490937 </pubmed></ref>。例えばシミュレーションによって、異なるメカニズムで働く神経回路から同じようなピーク位置、幅を持つ相互相関関数が得られる場合があることが示されている<ref name=brody />。
重要な関連語：室頂核、中位核、歯状核（小脳核の解説で）


==参考文献==
==参考文献==
<references/>


<references/>
 
（執筆者：塩崎博史、担当編集委員：藤田一郎）
 
例えば細胞Xと細胞Yが同期して活動していた場合、 <math>C_{XY}(\tau)</math> の値は <math>\tau = 0</math> で最大となる（図A）。

2012年5月2日 (水) 13:09時点における版

英語名：cross-correlation analysis

　相互相関解析とは、二つの時系列信号の類似度を、相互相関関数を用いて評価する方法である。神経科学の分野においては、主に細胞間の機能的結合を推定する目的で、同時計測した二つの神経細胞の活動に対して相互相関解析が行われる。

解析方法

　相互相関関数の定義は学問分野、研究者によって異なる。ここでは神経科学の分野でしばしば用いられる定義について述べる。

図１ 相互相関関数の例
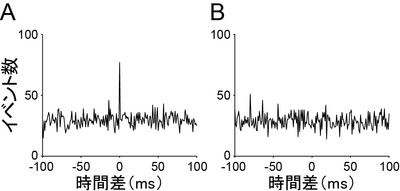
２つの仮想的な細胞のスパイク活動から計算した相互相関関数。平均10ヘルツで活動電位を発射する２つの細胞から5分間にわたり同時に活動を計測する実験をシミュレートし、相互相関関数を求めた。あるビンにおいて細胞が発火している状態を で、発火していない状態を で表した。A、２つの細胞が同期して活動する傾向がある場合、相互相関関数は時間差0にピークを持つ。B、２つの細胞の活動の間に何の関係性もない場合、相互相関関数は平坦となる

　ある二つの神経細胞の活動（例えば活動電位の発生タイミング）を同時に計測したとする。計測期間を 個のビンに区切り、 番目のビンにおけるある細胞の活動を で、もう一つの細胞の活動を で表す。このとき と の相互相関関数（相互相関ヒストグラム） は、次のように定義される。

ここで は と の間の時間差（time-lag）を表す。相互相関関数は、細胞 の活動と細胞 の活動との関係性を反映する（図１）。

　神経活動はしばしば確率過程としてモデル化される。この場合、相互相関関数の値は複数の統計量（細胞活動の平均や共分散）を反映する。例えば、二つの細胞の活動が独立、つまり共分散が0であっても、両細胞の活動の平均が時間的に同じように変化すると、相互相関関数は時間差0で最大となる場合がある（図２）。実験データから計算した相互相関関数と、二つの細胞の活動が独立である場合に期待される相互相関関数（帰無仮説）の差を取ることで、二つの細胞の活動が独立かどうかを統計的に検討することができる[1]。この差は相互共分散関数 と呼ばれる。

ここで と は 番目のビンにおける細胞 と細胞 の活動の平均を表す。関数 のことを相互相関関数と呼ぶ場合もあるので、注意が必要である。上のように定義した相互共分散関数の値は計測時間や平均活動度の違いによって変化する。異なる実験間で結果を比較するために、相互共分散関数の正規化が行われる場合がある[2]。

　 　 　スパイク活動の相関の有意性検定については、上記方法以外にも数多くの帰無仮説設定方法が考案されている[3]。

　なお

解釈

　相互共分散関数の形状から、神経回路の機能的結合関係を推定することができると考えられている。例えば、ある二つの細胞の活動から計算した相互共分散関数が時間差0に幅の狭い大きなピークを持つ場合、二つの細胞は共通の興奮性入力を受け取っていると考えられる[4][5]。また、相互共分散関数のピークの位置、幅を分析することにより、細胞間の興奮性結合や抑制性結合を推定することも可能である[1][5][6]。

　相互相関解析は機能的結合を間接的に推定する方法であるため、結果の解釈には曖昧性が残る可能性が指摘されている。例えば、異なるメカニズムで働く神経回路から、同じようなピーク位置、幅を持つ相互相関関数が得られる場合がある[1][7]。また、共通入力を受け取っていても、相互相関関数にピークが見られない場合もある[8]。

関連項目

同義語：覚醒中枢（脳幹網様体の解説で）

重要な関連語：室頂核、中位核、歯状核（小脳核の解説で）

参考文献

  1. ↑ 1.0 1.1 1.2 Perkel, D.H., Gerstein, G.L., & Moore, G.P. (1967).
    Neuronal spike trains and stochastic point processes. II. Simultaneous spike trains. Biophysical journal, 7(4), 419-40. [PubMed:4292792] [PMC] [WorldCat] [DOI]
  2. ↑ Bair, W., Zohary, E., & Newsome, W.T. (2001).
    Correlated firing in macaque visual area MT: time scales and relationship to behavior. The Journal of neuroscience : the official journal of the Society for Neuroscience, 21(5), 1676-97. [PubMed:11222658] [PMC] [WorldCat]
  3. ↑ Grün, S. (2009).
    Data-driven significance estimation for precise spike correlation. Journal of neurophysiology, 101(3), 1126-40. [PubMed:19129298] [PMC] [WorldCat] [DOI]
  4. ↑ Kimura, M., Tanaka, K., & Toyama, K. (1976).
    Interneuronal connectivity between visual cortical neurones of the cat as studied by cross-correlation analysis of their impulse discharges. Brain research, 118(2), 329-33. [PubMed:1000297] [WorldCat] [DOI]
  5. ↑ 5.0 5.1 Toyama, K., Kimura, M., & Tanaka, K. (1981).
    Cross-Correlation Analysis of Interneuronal Connectivity in cat visual cortex. Journal of neurophysiology, 46(2), 191-201. [PubMed:6267211] [WorldCat] [DOI]
  6. ↑ Tamura, H., Kaneko, H., Kawasaki, K., & Fujita, I. (2004).
    Presumed inhibitory neurons in the macaque inferior temporal cortex: visual response properties and functional interactions with adjacent neurons. Journal of neurophysiology, 91(6), 2782-96. [PubMed:14711977] [WorldCat] [DOI]
  7. ↑ Brody, C.D. (1999).
    Correlations without synchrony Neural computation, 11(7), 1537-51. [PubMed:10490937] [WorldCat]
  8. ↑ Renart, A., de la Rocha, J., Bartho, P., Hollender, L., Parga, N., Reyes, A., & Harris, K.D. (2010).
    The asynchronous state in cortical circuits. Science (New York, N.Y.), 327(5965), 587-90. [PubMed:20110507] [PMC] [WorldCat] [DOI]


（執筆者：塩崎博史、担当編集委員：藤田一郎）

例えば細胞Xと細胞Yが同期して活動していた場合、 の値は で最大となる（図A）。

「https://bsd.neuroinf.jp/w/index.php?title=相互相関解析&oldid=6852」から取得