「Förster共鳴エネルギー移動」の版間の差分
細 →原理 |
細編集の要約なし |
||
| 12行目: | 12行目: | ||
{{box|text= | {{box|text= | ||
2つの蛍光分子がごく近接して存在する場合、一つの蛍光分子からもう一つの蛍光分子へ、エネルギーが移行する。これをFörster共鳴エネルギー移動(FRET)という<ref><pubmed>22352636</pubmed></ref>。FRETの効率は2つの蛍光体のスペクトルの重なりの大きさ、距離と角度により左右される。この性質を利用し、タンパク質相互作用や細胞内シグナル伝達分子の可視化検出に用いられ、脳神経研究においても、神経細胞、脳スライスなどの組織および個体レベルで応用されている。 }} | |||
}} | |||
[[Image:FRET-図1.jpg|thumb|right|300px|<b>図1:蛍光体が蛍光を発する過程を示したヤブロンスキーダイヤグラム</b><br>青色で示した励起光によって、蛍光体の電子が励起状態に到達する。励起された電子は、回転および振動エネルギーを失いながら励起状態の最低準位に行き着く。この電子は緑色で示した蛍光を発して励起状態から基底状態に戻る。実際は、最低準位に行き着く前に基底状態に戻ることもあり、これが蛍光波長の幅に反映される。]] | [[Image:FRET-図1.jpg|thumb|right|300px|<b>図1:蛍光体が蛍光を発する過程を示したヤブロンスキーダイヤグラム</b><br>青色で示した励起光によって、蛍光体の電子が励起状態に到達する。励起された電子は、回転および振動エネルギーを失いながら励起状態の最低準位に行き着く。この電子は緑色で示した蛍光を発して励起状態から基底状態に戻る。実際は、最低準位に行き着く前に基底状態に戻ることもあり、これが蛍光波長の幅に反映される。]] | ||
| 21行目: | 20行目: | ||
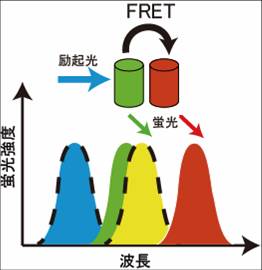
[[Image:FRET-図3.jpg|thumb|right|300px|<b>図3:ドナーの蛍光スペクトルとアクセプターの励起スペクトルに重なりがあるときに、FRETが起きる。黒破線で囲まれたスペクトルは、励起スペクトルを示す。緑色のタンパク質がドナー、赤色タンパク質がアクセプターを示す。</b>]] | [[Image:FRET-図3.jpg|thumb|right|300px|<b>図3:ドナーの蛍光スペクトルとアクセプターの励起スペクトルに重なりがあるときに、FRETが起きる。黒破線で囲まれたスペクトルは、励起スペクトルを示す。緑色のタンパク質がドナー、赤色タンパク質がアクセプターを示す。</b>]] | ||
== | ==Förster共鳴エネルギー移動とは== | ||
2つの蛍光分子がごく近接して存在する場合、一つの蛍光分子からもう一つの蛍光分子へ、エネルギーが移行する。この現象は、1946年[[wikipedia:Theodor Förster|Theodor Förster]]によって報告されたことから、Förster共鳴エネルギー移動(FRET)という<ref>'''Förster, T.'''<br>Energiewanderung und Fluorescenz<br>''Naturwissenscaft''. 1946, 33:166–175[[ファイル:Förster 1946.pdf PDF]]</ref><ref><pubmed>22352636</pubmed></ref>。かつてはFRETは、fluorescence resonance energy transferの略称として用いたが、実際には蛍光を伴わないエネルギー移動であることから、現在ではFörster resonance energy transferと呼ぶ事がIUPACにより推奨されている。 | |||
蛍光分子のうち、エネルギーを受け渡す方をドナー、受け取る方をアクセプターと呼ぶ。FRETの効率はドナー蛍光体とアクセプター蛍光体のスペクトルの重なりの大きさ、距離と角度により左右される。蛍光スペクトルが変化しない状態では、ドナーとアクセプター間の距離と角度の変化をFRETの効率の変化として読み取る事が出来る。緑色蛍光タンパク質(green fluorescent protein, GFP)とその色変異体や様々な蛍光スペクトルを持つ近縁のタンパク質の開発・同定によりFRETを用いて、生細胞の中の微小ドメインでのタンパク質相互作用、生化学反応や細胞内シグナル伝達の可視化が可能となった。 | |||
ドナーの蛍光団の電子が、励起光により[[wikipedia:ja:基底状態|基底状態]]から[[wikipedia:ja:励起状態|励起状態]]に励起される(図1)。励起された電子は、[[wikipedia:ja:回転エネルギー|回転エネルギー]]や[[wikipedia:ja:振動エネルギー|振動エネルギー]]を失いながら、励起状態の底まで行き着く。その後、基底状態に戻る際に、蛍光としてエネルギーを放出する。ドナーの近傍(数nmオーダー)に、ドナーの蛍光スペクトルと重なる励起スペクトルを持ったアクセプターが存在すると、FRETが起きる(図3)。FRETによって蛍光寿命の減少、ドナーの蛍光強度の減少、アクセプターの蛍光の増加などが観察される。 <br> FRETの速度定数<math>k_f \ </math>は、以下の式で規定される。 | |||
<br> <math>k_f(r,\kappa) = \frac{k_DQ_D\kappa^2}{r^6}\left(\frac{9000(In10)}{128\pi^5Nn^4}\right)\int_0^\infty F_D(\lambda)\epsilon_A(\lambda)\lambda^4\,d\lambda</math> | <br> <math>k_f(r,\kappa) = \frac{k_DQ_D\kappa^2}{r^6}\left(\frac{9000(In10)}{128\pi^5Nn^4}\right)\int_0^\infty F_D(\lambda)\epsilon_A(\lambda)\lambda^4\,d\lambda</math> | ||
| 31行目: | 34行目: | ||
#距離<math>r \ </math>。式が示すように距離の6乗に反比例する。FRET効率が50%になるときの距離を、フェルスター距離(Förster distance)という。 | #距離<math>r \ </math>。式が示すように距離の6乗に反比例する。FRET効率が50%になるときの距離を、フェルスター距離(Förster distance)という。 | ||
#ドナーの蛍光の遷移双極子モーメントとアクセプターの励起光の遷移双極子モーメントの配向<math>\kappa \ </math>。フルオレセインなど、等方的に蛍光の放射が起きる場合には、<math>\kappa^2 \ </math>=<math>\tfrac{2}{3} \ </math>であるが、GFPをはじめとした配向の定まった蛍光タンパク質などは各々の値を取る。 | #ドナーの蛍光の遷移双極子モーメントとアクセプターの励起光の遷移双極子モーメントの配向<math>\kappa \ </math>。フルオレセインなど、等方的に蛍光の放射が起きる場合には、<math>\kappa^2 \ </math>=<math>\tfrac{2}{3} \ </math>であるが、GFPをはじめとした配向の定まった蛍光タンパク質などは各々の値を取る。 | ||
蛍光の減衰曲線は、速度定数を<math>k \ </math>として、図2のように表すことができる。<math>N_0 \ </math>は励起光によって励起された電子の数、<math>k \ </math>は励起状態にある電子が基底状態に戻る速度定数であり、蛍光として基底状態に戻る際の速度定数、熱を発して基底状態に戻るなどの無放射遷移の速度定数の和として表される。今、 | |||
電子が起きる速度を<math>k_f \ </math>とすると、ドナーの励起された電子が基底状態に戻る速度定数は<math>k+k_f \ </math>となり、 | |||
== 検出 == | == 検出 == | ||
2013年10月21日 (月) 00:06時点における版
上田 善文
金沢医科大学 血液免疫内科学
林 康紀
独立行政法人理化学研究所 脳科学総合研究センター
DOI XXXX/XXXX 原稿受付日:2013年9月18日 原稿完成日:2013年月日
担当編集委員:柚崎 通介(慶應義塾大学 医学部生理学)
英:Förster resonance energy transfer 英略称:FRET 独:Förster-Resonanzenergietransfer 仏:transfert d'énergie entre molécules fluorescentes
2つの蛍光分子がごく近接して存在する場合、一つの蛍光分子からもう一つの蛍光分子へ、エネルギーが移行する。これをFörster共鳴エネルギー移動(FRET)という[1]。FRETの効率は2つの蛍光体のスペクトルの重なりの大きさ、距離と角度により左右される。この性質を利用し、タンパク質相互作用や細胞内シグナル伝達分子の可視化検出に用いられ、脳神経研究においても、神経細胞、脳スライスなどの組織および個体レベルで応用されている。
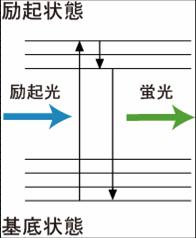
青色で示した励起光によって、蛍光体の電子が励起状態に到達する。励起された電子は、回転および振動エネルギーを失いながら励起状態の最低準位に行き着く。この電子は緑色で示した蛍光を発して励起状態から基底状態に戻る。実際は、最低準位に行き着く前に基底状態に戻ることもあり、これが蛍光波長の幅に反映される。
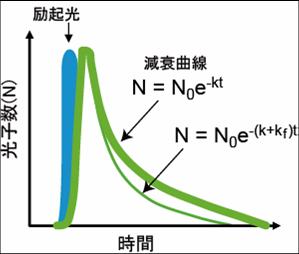
緑の太い線がFRETが起きていない時の減衰曲線。FRETの速度定数が加わることにより速度定数が大きくなり細い緑の線のように減衰曲線の傾斜が大きくなる。
Förster共鳴エネルギー移動とは
2つの蛍光分子がごく近接して存在する場合、一つの蛍光分子からもう一つの蛍光分子へ、エネルギーが移行する。この現象は、1946年Theodor Försterによって報告されたことから、Förster共鳴エネルギー移動(FRET)という[2][3]。かつてはFRETは、fluorescence resonance energy transferの略称として用いたが、実際には蛍光を伴わないエネルギー移動であることから、現在ではFörster resonance energy transferと呼ぶ事がIUPACにより推奨されている。
蛍光分子のうち、エネルギーを受け渡す方をドナー、受け取る方をアクセプターと呼ぶ。FRETの効率はドナー蛍光体とアクセプター蛍光体のスペクトルの重なりの大きさ、距離と角度により左右される。蛍光スペクトルが変化しない状態では、ドナーとアクセプター間の距離と角度の変化をFRETの効率の変化として読み取る事が出来る。緑色蛍光タンパク質(green fluorescent protein, GFP)とその色変異体や様々な蛍光スペクトルを持つ近縁のタンパク質の開発・同定によりFRETを用いて、生細胞の中の微小ドメインでのタンパク質相互作用、生化学反応や細胞内シグナル伝達の可視化が可能となった。
ドナーの蛍光団の電子が、励起光により基底状態から励起状態に励起される(図1)。励起された電子は、回転エネルギーや振動エネルギーを失いながら、励起状態の底まで行き着く。その後、基底状態に戻る際に、蛍光としてエネルギーを放出する。ドナーの近傍(数nmオーダー)に、ドナーの蛍光スペクトルと重なる励起スペクトルを持ったアクセプターが存在すると、FRETが起きる(図3)。FRETによって蛍光寿命の減少、ドナーの蛍光強度の減少、アクセプターの蛍光の増加などが観察される。
FRETの速度定数は、以下の式で規定される。
ここで、はドナーの蛍光の速度定数、はドナーの蛍光の量子収率、はドナーとアクセプターの双極子モーメントの配向、はドナーとアクセプターの距離、はアボガドロ数、は溶媒の屈折率、は規格化したドナーの発光強度、はアクセプターのモル吸光係数。
実際に、変数となりうるのは以下の性質である。
- 距離。式が示すように距離の6乗に反比例する。FRET効率が50%になるときの距離を、フェルスター距離(Förster distance)という。
- ドナーの蛍光の遷移双極子モーメントとアクセプターの励起光の遷移双極子モーメントの配向。フルオレセインなど、等方的に蛍光の放射が起きる場合には、=であるが、GFPをはじめとした配向の定まった蛍光タンパク質などは各々の値を取る。
蛍光の減衰曲線は、速度定数をとして、図2のように表すことができる。は励起光によって励起された電子の数、は励起状態にある電子が基底状態に戻る速度定数であり、蛍光として基底状態に戻る際の速度定数、熱を発して基底状態に戻るなどの無放射遷移の速度定数の和として表される。今、
電子が起きる速度をとすると、ドナーの励起された電子が基底状態に戻る速度定数はとなり、
検出
ドナーとアクセプターの蛍光強度比を測定する方法
ドナーおよびアクセプターの蛍光を取得後、ドナーとアクセプターの蛍光強度比が計算される。FRETが起きると、ドナーの蛍光強度が減少し、アクセプターの蛍光強度が増加する。現在、最も広く使用されている手法である。データを取得、解釈する際に注意しなければいけないポイントがある。
まず、ドナーの蛍光のアクセプターチャネルへの漏れ込みであり、SN比の減少の原因となる。改善点としては漏れ込みを極力抑える適切なバンドパスフィルターを用いることである。また、ドナーおよびアクセプターのバックグラウンドが、FRET変化に影響を与える。サブトラクションすることで、より正しいFRET効率が得られる。次に、2分子間FRETで起きることであるが、ドナーとアクセプターの局在の違いは疑似FRETを生じる。リンカーで連結し1分子にすること、局在しているアクセプターの蛍光強度を計算することで修正することが可能である。現在、多数の遺伝子工学的に作製されたタンパク質FRETプローブにおいて、GFPの色彩変異体、シアン色蛍光タンパク質CFPと黄色蛍光タンパク質YFPのFRETペアが広範に用いられている。近年、CloverとmRuby2が開発され、より良いFRETペアであると報告されている[4]。
アクセプターブリーチング法
適切な波長によって、アクセプターを退色させることでFRETを解消することができる。
この解消度合いより生じていたFRETを算出する。この手法は不可逆的であるために経時的変化を追うことは困難である。
ドナーの蛍光寿命を測定する方法
蛍光体が励起されると、図2に示すような減衰曲線に従って蛍光を発する。蛍光寿命は、蛍光の減衰曲線の速度定数と逆数の関係にある。 蛍光寿命は、GFPは2.5nsec、YFPでは2.9nsec、mCherryでは1.5nsecの値を取る。FRETが起きるとドナーの蛍光寿命が減少する(図4)。
FRETが起きると、蛍光寿命が減少する。蛍光寿命の変化を測定する方法は2つある。
Time domainおよびfrequency domainである。Time domainについては、近年、データ処理速度の向上により、メガヘルツオーダーのパルス励起光によって励起された一つ一つの光子を、迅速に検出する時間相関単一光子計数法が発展してきた。励起光によって発生した一つ一つの光子が検出器まで届くまでの時間(数nsec)の確率分布が減衰曲線を形成するため、時間を横軸としてヒストグラムを作製することができる。Double exponetial fittingによって、FRETの起きている割合が算出できる。Time domainは、フーリエ変換によってfrequency domainに変換可能である。蛍光寿命プローブとして、ドナーとしてmGFP、アクセプターとしてmRFPもしくはmCherryが用いられる。アクセプターの蛍光は必要ないため、FRETのアクセプターとなるが蛍光を発しないREACh, dark Venus, super REAChなども用いられる。蛍光寿命は、蛍光強度比測定法に比べて、蛍光の漏れ込み、アクセプターとの局在の違いなどによって生じる疑似FRETを回避できる。取得した蛍光を理論上全てデータに反映させることができるが、実際には、time domainにおいて、光子取得後、再び光子を取得する状態に戻るハードウェアのリセット時間(dead time)などがあり全ての光子を取得するには、改善の余地がある。また、秒単位の経時変化を追うためには、64X64ピクセルで画像取得されているのが現状で有り、多数のピクセルから蛍光寿命を取得するためには、処理速度の速いハードウェアが必要となる。さらに、短時間で画像を取得するためには、明るいサンプルであったほうがよい。
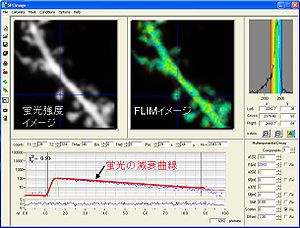
(横軸は時間、縦軸は光子数)をBecker&Hickl社software、SPC imageにて取得した。実際には、20秒で数千個オーダーの光子を取得する。これらの光子の発生確率分布が減衰曲線を形成し、近似曲線をフィッティングさせることで蛍光寿命を取得する。
異方性を測定する方法
一つの蛍光団のストークスシフトが小さい場合、励起スペクトルと蛍光スペクトルの重なりが大きい。このような蛍光団では、同一の蛍光団同士で、Homo-FRETが生じる。Homo-FRETは、蛍光強度および蛍光寿命は変化しないが、異方性が変わる。この原理を用いて、一般的には、分子同士のクラスターの度合いなどに応用されている。
プローブのデザイン
神経科学分野を始めとして、様々な細胞生物学の分野において、多くの蛍光タンパク質を基にしたFRETプローブが使用されている。これらのプローブを分類すると、以下のように分類される。
プローブの分解に伴うFRETの変化を検出するプローブ
この原理は、FRETプローブの最も初期に導入されたデザインである。例として、Factor Xなどのプロテアーゼが挙げられ[5]、プロテアーゼによって分解される配列の両端にドナーとアクセプターを連結する。プロテアーゼによって、この配列が分解されるとドナーとアクセプターの間に起きていたFRETが解消されることによって、プロテアーゼの活性を評価する。カスパーゼなどの活性を測定するためにも使用されている[6][7][8][9]。このプローブのデザインの短所としては、反応が不可逆的であるために、一つの実験系で何度も測定することが困難であることである。
2分子間相互作用を利用したFRETプローブ
興味のあるタンパク質同士の相互作用を測定する際に、この原理が用いられる。一方にドナー、他方にアクセプターを連結する。タンパク質同士が結合していないときにはFRETは起きていないが、結合することによってFRETを生じる。応用例としては蛍光寿命を基にしたGタンパク質の活性化の測定に用いられている[10]。また、アクチンの重合度を測定するために、アクチンにドナー、アクセプターを連結して測定している例もある[11]。 距離のファクターを生かせるために、比較的大きなシグナルが得られる一方、内在性のタンパク質が反応に関与するために、その分FRET応答が減少する。ドナーとアクセプターの発現量の差によるFRETの応答の変化も問題になる。特に、アクセプターと結合しないドナーが多量に存在するとFRET応答が小さくなる。一般にアクセプターが多い系が、使用に適している。
一分子内FRETプローブ
一分子内にドナーとアクセプターを連結し、これらの配向および距離の変化を利用する。2分子間FRETに生じるような発現量の違いやドナーとアクセプターの局在の変化によって生じるアーチファクトなどを考慮する必要がない。さらに活性に伴うタンパク質の構造変化などを利用するために、比較的容易に応答するプローブが作製できるが、ドナーとアクセプターを適切な位置に配置するなどの検討が必要である。
タンパク質の構造変化を基にしたFRETプローブ
興味のあるタンパク質が、活性化の際に構造変化を誘起することが知られている場合には構造変化を利用することができる。タンパク質のC末およびN末にドナーおよびアクセプターを連結する。この手法は、CaMKII[12]、Calcinulin[13]、raf[14][15]、膜電位測定[16]、などに用いられている。
タンパク質結合に伴う構造変化を基にしたFRETプローブ
ある種のタンパク質は活性化、非活性化に伴い、下流のタンパク質と結合する。このような相互作用を利用してタンパク質の活性化、非活性化を測定することができる。低分子G-proteinの活性化を測定するためにも用いられている。カルシウムFRETプローブ、カメレオンはこの原理を利用している[17]。 また、G-proteinの活性化プローブは、ドナー、アクセプター、G-protein、シグナル伝達下流の結合タンパク質の結合ドメインからなる。G-proteinがGDPからGTP結合型になり活性化すると、結合ドメインと相互作用をしFRETが生じる[18]。
共有結合修飾によって生じる構造変化を測定するプローブ
このプローブは、ドナー、アクセプター、共有結合修飾を受けるドメイン、これを認識するドメインからなる。プローブが共有結合修飾を受けると、認識するドメインが結合し、ドナーとアクセプターの距離が縮まりFRETが起きる。このプローブは、キナーゼの活性化を測定するために使用される[19][20]。
生体膜上の小分子を測定するFRETプローブ
このプローブは、主に、脂質分子に応用されてきた。ドナー、脂質結合ドメイン、アクセプターが堅いヘリックス構造で連結され、グリシングリシン配列をその途中に導入することで、そこを中心に一方の蛍光タンパク質が回転することができる。膜結合ドメインを用いて、プローブを結合させる。脂質分子が増えた際に、脂質結合ドメインが脂質分子を認識し、構造変化が起き、ドナートアクセプターの距離が縮まりFRETが生じる。ジアシルグリセロール[21], イノシトールリン脂質群[22][23][24][25]を測定するために用いられている。
神経科学分野への応用
1992年、GFPのクローニングにより[26]、生きた細胞において、細胞内のオルガネラ、タンパク質などの蛍光標識が容易になった。青色蛍光タンパク質CFP、YFPなどの色彩変異体の開発も進み、FRETプローブを作製する土壌ができあがった。
1997年、宮脇、Tsienらによって、CFPおよびYFPを利用した、Calcium indicator, Cameleonが開発され[27]、さらに、cAMP[28], cGMP[29], リン酸化[30]を初めとした主要な細胞内シグナル伝達分子のFRETプローブが次々と作製され、分子のリアルタイムな活性および局在のの活性の解明に大きく貢献した。
脳神経分野においては、林らが、2000年初期に記憶の形成に必須なシグナル分子、カルシウムカルモデュリンキナーゼII (CaMKII)の活性化を評価するためのFRETプローブ開発し分散培養系にてCaMkIIの可視化に成功した[31]。1990年代後半、Svobodaらによって、2光子顕微鏡が脳神経科学に導入され、神経回路ネットワークを保持したスライスおよび個体の生きた脳の神経活動を観察可能になった。林らは、神経細胞の連結部位、シナプスのシナプス後膜(スパイン)において、その形態を制御するactinの重合を可視化するためのFRETプローブを開発した[32]。一方、脳のスライスにおいては、波長依存的な蛍光の吸収が生じるため、ドナーとアクセプターの2波長を測定する蛍光強度比を測定するよりも、蛍光の散乱、吸収によって変化しない蛍光寿命測定法が導入された。安田、Svobodaらは、蛍光寿命測定を基に、スパインの構造的変化を誘導する低分子量Gタンパク質(Ras、cdc42、RhoA)などのシグナル伝達分子の活性化の変化を観察することに成功している[33][34][35]。
個体においてもFRET測定法が導入されている。神経回路ネットワークにおけるシナプスの役割を解明する目的で、フェレットの大脳皮質視覚野にCaMKIIプローブを発現し、片眼剥奪によって、神経回路ネットワークに変化を起こした時のCaMKIIの活性化の変化を観測している[36]。また、神経活動をモニターする目的で、Knöpfelらは、膜電位プローブを開発しマウスのヒゲ刺激の入力先である体性感覚野barrel cortexでの入力特異的な神経の活性化を観察している[37]。
病態との関係では、神経細胞内のカルシウム濃度を測定するために、オレゴングリーンの蛍光寿命の変化から、カルシウム濃度を測定し、アストロサイトでのカルシウム濃度が、アルツハイマー様マウスと正常マウスで違うことが報告されている[38]。
Homo-FRETも応用されている。CaMKIIは12量体を形成しているが、異方性の変化を基に、その構造中にdimerの単位が存在し、活性化に伴うdimer同士の位置関係が変化することをVogelらが明らかにしている[39]。
将来展望
脳研究は、生きたままの状態の脳の神経細胞の活動を、広範囲で、より深部で観察したり、逆に神経細胞内の超微細構造を観察する方向に移るであろう。現在、FRETを基にしたin vivoイメージングは、応答の低さ、蛍光の弱さなどの難点はあるものの、蛍光タンパク質の蛍光強度や顕微鏡の性能の改良は日進月歩であり改善されていくであろう。また、神経活動に必要なシグナル伝達を同時に観察するために、マルチカラーイメージングの試みもなされるであろう。その際には、2つの波長を必要とする蛍光強度比変化を基にするFRET測定よりも、蛍光寿命を観察するFLIM測定が適している。
参考文献
- ↑
Förster, T. (2012).
Energy migration and fluorescence. 1946. Journal of biomedical optics, 17(1), 011002. [PubMed:22352636] [WorldCat] [DOI] - ↑ Förster, T.
Energiewanderung und Fluorescenz
Naturwissenscaft. 1946, 33:166–175ファイル:Förster 1946.pdf PDF - ↑
Förster, T. (2012).
Energy migration and fluorescence. 1946. Journal of biomedical optics, 17(1), 011002. [PubMed:22352636] [WorldCat] [DOI] - ↑
Lam, A.J., St-Pierre, F., Gong, Y., Marshall, J.D., Cranfill, P.J., Baird, M.A., ..., & Lin, M.Z. (2012).
Improving FRET dynamic range with bright green and red fluorescent proteins. Nature methods, 9(10), 1005-12. [PubMed:22961245] [PMC] [WorldCat] [DOI] - ↑
Mitra, R.D., Silva, C.M., & Youvan, D.C. (1996).
Fluorescence resonance energy transfer between blue-emitting and red-shifted excitation derivatives of the green fluorescent protein. Gene, 173(1 Spec No), 13-7. [PubMed:8707050] [WorldCat] [DOI] - ↑
Xu, X., Gerard, A.L., Huang, B.C., Anderson, D.C., Payan, D.G., & Luo, Y. (1998).
Detection of programmed cell death using fluorescence energy transfer. Nucleic acids research, 26(8), 2034-5. [PubMed:9518501] [PMC] [WorldCat] [DOI] - ↑
Onuki, R., Nagasaki, A., Kawasaki, H., Baba, T., Uyeda, T.Q., & Taira, K. (2002).
Confirmation by FRET in individual living cells of the absence of significant amyloid beta -mediated caspase 8 activation. Proceedings of the National Academy of Sciences of the United States of America, 99(23), 14716-21. [PubMed:12409609] [PMC] [WorldCat] [DOI] - ↑
Joseph, J., Seervi, M., Sobhan, P.K., & Retnabai, S.T. (2011).
High throughput ratio imaging to profile caspase activity: potential application in multiparameter high content apoptosis analysis and drug screening. PloS one, 6(5), e20114. [PubMed:21637712] [PMC] [WorldCat] [DOI] - ↑
Li, I.T., Chiang, J.J., & Truong, K. (2006).
FRET evidence that an isoform of caspase-7 binds but does not cleave its substrate. Conference proceedings : ... Annual International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE Engineering in Medicine and Biology Society. Annual Conference, 1, 531-4. [PubMed:17946841] [WorldCat] [DOI] - ↑
Mochizuki, N., Yamashita, S., Kurokawa, K., Ohba, Y., Nagai, T., Miyawaki, A., & Matsuda, M. (2001).
Spatio-temporal images of growth-factor-induced activation of Ras and Rap1. Nature, 411(6841), 1065-8. [PubMed:11429608] [WorldCat] [DOI] - ↑
Okamoto, K., Nagai, T., Miyawaki, A., & Hayashi, Y. (2004).
Rapid and persistent modulation of actin dynamics regulates postsynaptic reorganization underlying bidirectional plasticity. Nature neuroscience, 7(10), 1104-12. [PubMed:15361876] [WorldCat] [DOI] - ↑
Takao, K., Okamoto, K., Nakagawa, T., Neve, R.L., Nagai, T., Miyawaki, A., ..., & Hayashi, Y. (2005).
Visualization of synaptic Ca2+ /calmodulin-dependent protein kinase II activity in living neurons. The Journal of neuroscience : the official journal of the Society for Neuroscience, 25(12), 3107-12. [PubMed:15788767] [PMC] [WorldCat] [DOI] - ↑
Newman, R.H., & Zhang, J. (2008).
Visualization of phosphatase activity in living cells with a FRET-based calcineurin activity sensor. Molecular bioSystems, 4(6), 496-501. [PubMed:18493642] [WorldCat] [DOI] - ↑
Terai, K., & Matsuda, M. (2005).
Ras binding opens c-Raf to expose the docking site for mitogen-activated protein kinase kinase. EMBO reports, 6(3), 251-5. [PubMed:15711535] [PMC] [WorldCat] [DOI] - ↑
Terai, K., & Matsuda, M. (2006).
The amino-terminal B-Raf-specific region mediates calcium-dependent homo- and hetero-dimerization of Raf. The EMBO journal, 25(15), 3556-64. [PubMed:16858395] [PMC] [WorldCat] [DOI] - ↑
Tsutsui, H., Karasawa, S., Okamura, Y., & Miyawaki, A. (2008).
Improving membrane voltage measurements using FRET with new fluorescent proteins. Nature methods, 5(8), 683-5. [PubMed:18622396] [WorldCat] [DOI] - ↑
Miyawaki, A., Llopis, J., Heim, R., McCaffery, J.M., Adams, J.A., Ikura, M., & Tsien, R.Y. (1997).
Fluorescent indicators for Ca2+ based on green fluorescent proteins and calmodulin. Nature, 388(6645), 882-7. [PubMed:9278050] [WorldCat] [DOI] - ↑
Yasuda, R., Harvey, C.D., Zhong, H., Sobczyk, A., van Aelst, L., & Svoboda, K. (2006).
Supersensitive Ras activation in dendrites and spines revealed by two-photon fluorescence lifetime imaging. Nature neuroscience, 9(2), 283-91. [PubMed:16429133] [WorldCat] [DOI] - ↑
Sato, M., Ozawa, T., Inukai, K., Asano, T., & Umezawa, Y. (2002).
Fluorescent indicators for imaging protein phosphorylation in single living cells. Nature biotechnology, 20(3), 287-94. [PubMed:11875431] [WorldCat] [DOI] - ↑
Ting, A.Y., Kain, K.H., Klemke, R.L., & Tsien, R.Y. (2001).
Genetically encoded fluorescent reporters of protein tyrosine kinase activities in living cells. Proceedings of the National Academy of Sciences of the United States of America, 98(26), 15003-8. [PubMed:11752449] [PMC] [WorldCat] [DOI] - ↑
Sato, M., Ueda, Y., & Umezawa, Y. (2006).
Imaging diacylglycerol dynamics at organelle membranes. Nature methods, 3(10), 797-9. [PubMed:16990811] [WorldCat] [DOI] - ↑
Sato, M., Ueda, Y., Takagi, T., & Umezawa, Y. (2003).
Production of PtdInsP3 at endomembranes is triggered by receptor endocytosis. Nature cell biology, 5(11), 1016-22. [PubMed:14528311] [WorldCat] [DOI] - ↑
Nishioka, T., Aoki, K., Hikake, K., Yoshizaki, H., Kiyokawa, E., & Matsuda, M. (2008).
Rapid turnover rate of phosphoinositides at the front of migrating MDCK cells. Molecular biology of the cell, 19(10), 4213-23. [PubMed:18685081] [PMC] [WorldCat] [DOI] - ↑
Nishioka, T., Aoki, K., Hikake, K., Yoshizaki, H., Kiyokawa, E., & Matsuda, M. (2008).
Rapid turnover rate of phosphoinositides at the front of migrating MDCK cells. Molecular biology of the cell, 19(10), 4213-23. [PubMed:18685081] [PMC] [WorldCat] [DOI] - ↑
Nishioka, T., Aoki, K., Hikake, K., Yoshizaki, H., Kiyokawa, E., & Matsuda, M. (2008).
Rapid turnover rate of phosphoinositides at the front of migrating MDCK cells. Molecular biology of the cell, 19(10), 4213-23. [PubMed:18685081] [PMC] [WorldCat] [DOI] - ↑
Prasher, D.C., Eckenrode, V.K., Ward, W.W., Prendergast, F.G., & Cormier, M.J. (1992).
Primary structure of the Aequorea victoria green-fluorescent protein. Gene, 111(2), 229-33. [PubMed:1347277] [WorldCat] [DOI] - ↑
Miyawaki, A., Llopis, J., Heim, R., McCaffery, J.M., Adams, J.A., Ikura, M., & Tsien, R.Y. (1997).
Fluorescent indicators for Ca2+ based on green fluorescent proteins and calmodulin. Nature, 388(6645), 882-7. [PubMed:9278050] [WorldCat] [DOI] - ↑
Zaccolo, M., De Giorgi, F., Cho, C.Y., Feng, L., Knapp, T., Negulescu, P.A., ..., & Pozzan, T. (2000).
A genetically encoded, fluorescent indicator for cyclic AMP in living cells. Nature cell biology, 2(1), 25-9. [PubMed:10620803] [WorldCat] [DOI] - ↑
Sato, M., Hida, N., Ozawa, T., & Umezawa, Y. (2000).
Fluorescent indicators for cyclic GMP based on cyclic GMP-dependent protein kinase Ialpha and green fluorescent proteins. Analytical chemistry, 72(24), 5918-24. [PubMed:11140757] [WorldCat] [DOI] - ↑
Ting, A.Y., Kain, K.H., Klemke, R.L., & Tsien, R.Y. (2001).
Genetically encoded fluorescent reporters of protein tyrosine kinase activities in living cells. Proceedings of the National Academy of Sciences of the United States of America, 98(26), 15003-8. [PubMed:11752449] [PMC] [WorldCat] [DOI] - ↑
Takao, K., Okamoto, K., Nakagawa, T., Neve, R.L., Nagai, T., Miyawaki, A., ..., & Hayashi, Y. (2005).
Visualization of synaptic Ca2+ /calmodulin-dependent protein kinase II activity in living neurons. The Journal of neuroscience : the official journal of the Society for Neuroscience, 25(12), 3107-12. [PubMed:15788767] [PMC] [WorldCat] [DOI] - ↑
Okamoto, K., Nagai, T., Miyawaki, A., & Hayashi, Y. (2004).
Rapid and persistent modulation of actin dynamics regulates postsynaptic reorganization underlying bidirectional plasticity. Nature neuroscience, 7(10), 1104-12. [PubMed:15361876] [WorldCat] [DOI] - ↑
Lee, S.J., Escobedo-Lozoya, Y., Szatmari, E.M., & Yasuda, R. (2009).
Activation of CaMKII in single dendritic spines during long-term potentiation. Nature, 458(7236), 299-304. [PubMed:19295602] [PMC] [WorldCat] [DOI] - ↑
Harvey, C.D., Yasuda, R., Zhong, H., & Svoboda, K. (2008).
The spread of Ras activity triggered by activation of a single dendritic spine. Science (New York, N.Y.), 321(5885), 136-40. [PubMed:18556515] [PMC] [WorldCat] [DOI] - ↑
Murakoshi, H., Wang, H., & Yasuda, R. (2011).
Local, persistent activation of Rho GTPases during plasticity of single dendritic spines. Nature, 472(7341), 100-4. [PubMed:21423166] [PMC] [WorldCat] [DOI] - ↑
Mower, A.F., Kwok, S., Yu, H., Majewska, A.K., Okamoto, K., Hayashi, Y., & Sur, M. (2011).
Experience-dependent regulation of CaMKII activity within single visual cortex synapses in vivo. Proceedings of the National Academy of Sciences of the United States of America, 108(52), 21241-6. [PubMed:22160721] [PMC] [WorldCat] [DOI] - ↑
Akemann, W., Mutoh, H., Perron, A., Rossier, J., & Knöpfel, T. (2010).
Imaging brain electric signals with genetically targeted voltage-sensitive fluorescent proteins. Nature methods, 7(8), 643-9. [PubMed:20622860] [WorldCat] [DOI] - ↑
Kuchibhotla, K.V., Lattarulo, C.R., Hyman, B.T., & Bacskai, B.J. (2009).
Synchronous hyperactivity and intercellular calcium waves in astrocytes in Alzheimer mice. Science (New York, N.Y.), 323(5918), 1211-5. [PubMed:19251629] [PMC] [WorldCat] [DOI] - ↑
Thaler, C., Koushik, S.V., Puhl, H.L., Blank, P.S., & Vogel, S.S. (2009).
Structural rearrangement of CaMKIIalpha catalytic domains encodes activation. Proceedings of the National Academy of Sciences of the United States of America, 106(15), 6369-74. [PubMed:19339497] [PMC] [WorldCat] [DOI]














