「反応時間」の版間の差分
細編集の要約なし |
Niimiryosuke (トーク | 投稿記録) 細編集の要約なし |
||
| (3人の利用者による、間の11版が非表示) | |||
| 1行目: | 1行目: | ||
英:reaction time/response time、英略語:RT | |||
英:reaction time/response | |||
同義語:反応潜時 | 同義語:反応潜時 | ||
反応時間とは、生体に刺激が与えられてからその刺激に対する外的に観察可能な反応が生じるまでの時間である。 | |||
特に、ヒトが何らかの知覚・認知課題を遂行する際の、随意的行動による反応について言う(例えば、ランプが点灯したらすぐボタンを押す)。 | |||
類義語に潜時(latency)があるが、これは反応時間より広い概念で、ヒト以外の動物の反応や、 | |||
行動ではなく生理指標として観察される反応についても言う(例えば、視覚刺激提示から視覚[[誘発電位]]が生じるまでの時間)。 | |||
ここでは、ヒトの行動実験における反応時間について概説する。 | |||
反応時間は課題遂行成績(performance)の重要な指標である。 | |||
反応時間が長いほど、複雑で多くの心的処理を要したと考えられる。 | |||
ただし、反応時間は刺激の入力から反応の出力までに起こる種々の処理過程を総体として反映する指標である。 | |||
それらは少なくとも刺激の知覚、判断や反応選択、反応のための運動実行の3つに分けられるが、いずれの処理段階も反応時間に影響を生じうる。 | |||
なお、反応時間の平均的な長さだけでなく、ばらつき(標準偏差など)が分析されることもある。 | |||
==いろいろな反応時間== | ==いろいろな反応時間== | ||
[[ファイル:RTfprtmt.png| | [[ファイル:RTfprtmt.png|frame|'''図1.''' 反応時間と運動時間(MT)、先行期間(FP)。例として、予告刺激の音が鳴った後、 | ||
反応刺激として左右どちらかのランプ(□)が点灯し、点灯した方のボタン(○)をできるだけ速く押す(押すとランプは消灯)という課題の場合を示す。 | |||
あらかじめボタン上に指を置き、指の動きだけで反応する場合(上段)では、反応刺激提示からボタン押しまでの時間を反応時間とする。 | |||
指をスタート位置から動かして(リーチング動作)ボタンを押す場合(下段)では、運動開始までを反応時間とすることが多い。 | |||
ただし、運動時間も含めて反応時間と呼ぶこともある。]] | |||
反応時間測定では、手指ボタン押し反応のほか、 | |||
足のペダル押し、発声、[[眼球運動]]なども用いられる | |||
<ref>[[眼球運動]]の場合には反応時間ではなく潜時と呼ぶことが多い。</ref> | |||
。 | |||
リーチング | |||
<ref> | |||
英:reaching、到達運動。目標となる物体に向けて手をのばす、あるいは手をのばして触れる行動。 | |||
</ref> | |||
のような動作に比較的時間のかかる反応では、刺激提示から運動開始までを反応時間、 | |||
運動開始から終了までを運動時間(movement time, MT)と呼んで区別することもある(図1)。 | |||
短距離走のスタートのような全身運動による反応については、全身反応時間(whole body reaction time)と呼ぶ。 | |||
例えば、刺激が提示されたらできるだけ速く跳び上がらせ(垂直跳び課題)、両足が地を離れるまでの時間として測定する。 | |||
ただし、単純な反応動作でも多数の筋肉が関与するものである。 | |||
[[EMG]]で筋肉の運動潜時を調べると、反応時間と一致するとは限らないし、筋によっても差がある | |||
<ref name=MorenoEtal2011><pubmed> 21184808 </pubmed></ref>。 | |||
===課題による分類=== | ===課題による分類=== | ||
一般に反応時間測定では、できるだけ速く反応する課題(speeded task)を用いる。 | |||
これに対し、好きな時に反応してよい課題の反応時間は自由反応時間(free reaction time)と呼んで区別することがある。 | |||
また、課題の内容に応じて、次の3種類が区別される。 | |||
====単純反応時間(simple reaction time, SRT)<ref>古い文献では簡単反応時間と訳されることがある。</ref>==== | |||
既知の1種の刺激が提示され、それに対して決められた1種の反応をする(単純検出課題)ときの反応時間。 | |||
例えば、音が聞こえたらできるだけ速くボタンを押す。 | |||
下の2種よりも平均的には短く、視覚ないし聴覚刺激に対するボタン押しでは150~300ms程度である。 | |||
==== | ====選択反応時間(choice reaction time, CRT)==== | ||
既知の複数の刺激のいずれかが提示され、刺激に応じて決められた複数の反応のいずれかを行う | |||
(n肢強制選択課題; n-alternative forced choice task, nAFC task)ときの反応時間。 | |||
例えば、緑光か赤光が提示され、緑なら右、赤なら左のボタンをできるだけ速く押す(2肢強制選択課題; 2AFC task)。 | |||
==== | ====Go/No-Go反応時間(Go/No-Go reaction time)==== | ||
Go/No-Go reaction | |||
弁別反応時間(discriminative reaction time)とも。 | |||
既知の複数の刺激のいずれかが提示され、そのうち特定の刺激の場合のみ、決められた1種の反応をするときの反応時間。 | |||
例えば、緑光か赤光が提示され、緑ならボタンを押し、赤なら何もしない。 | |||
つまり、反応するかしないか(Go/No-Go)を判断する。 | |||
==初期の研究== | ==初期の研究== | ||
| 53行目: | 69行目: | ||
===神経伝達速度の測定=== | ===神経伝達速度の測定=== | ||
反応時間測定は19世紀末の実験心理学成立当初から行われている。 | |||
'''E G Boring'''<br>A history of experimental psychology (2nd ed.)<br>''New York: Appleton-Century-Crofts'': 1950, p. 147</ref>。 | 現在では反応時間は研究の手段として用いられることが多いが、当時は反応時間自体が研究対象だった。 | ||
生理学者や心理学者が、心的処理の速さはどれくらいかを測ろうとしたのである。 | |||
19世紀末は心的時間測定(mental chronometry)の時代であった | |||
<ref> | |||
'''E G Boring'''<br> | |||
A history of experimental psychology (2nd ed.)<br> | |||
''New York: Appleton-Century-Crofts'': 1950, p. 147 | |||
</ref> | |||
。 | |||
直接の契機は、1849~1850年に[[wikipedia:ja:ヘルマン・フォン・ヘルムホルツ|ヘルムホルツ]]が | |||
<ref>'''K M Olesko, F L Holmes'''<br>Experiment, quantification, and discovery: Helmholtz's early physiological researches, 1843-50.<br> | カエル運動神経伝達速度を毎秒24.6~35.4mと測定したことだった | ||
In David Cahan (ed), Hermann von Helmholtz and the foundations of nineteenth-century science.<br>''Berkeley: University of California Press'': 1993, pp. 50-108.</ref><ref><pubmed>12122806</pubmed></ref><ref>実際には、[[活動電位]]の伝達速度は[[髄鞘]] | <ref> | ||
ヒトの場合、遅いものでは毎秒0.5~2m、速いものでは最大毎秒75mに達する。</ref> | '''K M Olesko, F L Holmes'''<br> | ||
Experiment, quantification, and discovery: Helmholtz's early physiological researches, 1843-50.<br> | |||
In David Cahan (ed), Hermann von Helmholtz and the foundations of nineteenth-century science.<br> | |||
''Berkeley: University of California Press'': 1993, pp. 50-108. | |||
</ref> | |||
<ref><pubmed>12122806</pubmed></ref> | |||
<ref> | |||
実際には、[[活動電位]]の伝達速度は[[髄鞘]]の有無や神経線維の太さによって大きく異なる。 | |||
ヒトの場合、遅いものでは毎秒0.5~2m、速いものでは最大毎秒75mに達する。 | |||
</ref> | |||
。 | |||
私たちは日常的には、自分が意図した瞬間に体が動き、心的処理は「瞬時に」完了すると思っている。 | |||
これに反して神経の働きは意外に遅く、十分測定可能な程度の速さでしかなかったのである。 | |||
===ドンデルスの減算法=== | ===ドンデルスの減算法=== | ||
では、知覚や判断はどれくらいの速さなのだろうか。 | |||
''Nieuwkoop: B. de Graaf'': 1970, pp. 33-73.</ref><ref name=Donders1868><pubmed>5811531</pubmed></ref> | ヒトでの反応時間研究の嚆矢はオランダの[[wikipedia:Franciscus_Donders|ドンデルス]]らによる1860年代の実験 | ||
<ref name=deJaager1865> | |||
'''J J de Jaager'''<br> | |||
Reaction time and mental processes.<br> | |||
In J Brozek, M S Sibinga (eds.), Origins of psychometry.<br> | |||
''Nieuwkoop: B. de Graaf'': 1970, pp. 33-73. | |||
</ref> | |||
<ref name=Donders1868><pubmed>5811531</pubmed></ref> | |||
とされる。 | |||
彼らは、反応時間のうち本当に心的処理(mental process)に要した時間を測ろうとした。 | |||
例えば、緑光に対して右、赤光に対して左のボタンを押す課題で、反応時間が仮に300msだとしても、色弁別の心的処理に300msかかるとは言えない。 | |||
そのうち相応の部分は、[[網膜]]から脳への伝達時間や脳から手の筋肉への伝達時間のはずだからである。 | |||
ドンデルスらは、減算法(subtraction method)と呼ばれる方法でこの問題に取り組んだ。 | |||
音声を聞いたらできるだけ速く発声して反応するという課題を使い、以下の反応時間を測定した。 | |||
*単純反応時間。''ki''に対して、できるだけ速く''ki''と発声して反応する。 | *単純反応時間。''ki''に対して、できるだけ速く''ki''と発声して反応する。 | ||
| 72行目: | 120行目: | ||
*弁別反応時間。''ka, ke, ki, ko, ku''のいずれかが提示され、''ki''の場合のみ''ki''と発声して反応する。 | *弁別反応時間。''ka, ke, ki, ko, ku''のいずれかが提示され、''ki''の場合のみ''ki''と発声して反応する。 | ||
結果は、順に平均201ms、284ms、237msとなった<ref name=Donders1868 />。 | |||
選択反応時間から単純反応時間を引いた差83msは、刺激の弁別と反応の選択の心的処理に要した時間と考えられる。 | |||
選択反応時間から弁別反応時間を引いた差47msは、反応の選択の心的処理に要した時間と考えられる | |||
(弁別課題では反応の選択は必要ないが、刺激の弁別は必要である)。 | |||
このように条件間の減算で心的処理に要する時間を推定するのが減算法である。 | |||
しかし、この試みはうまくいかなかった。 | |||
反応時間に影響を与える要因が多すぎるのである。個人差も大きい。 | |||
何より、知覚や認知といった心的処理を構成要素の単純な加算で考えることに限界があった。 | |||
今日よく知られているように神経系の情報処理は高度に並列的である。 | |||
また、用いた課題がどんな心的処理を含むのかについては解釈に幅がある。 | |||
例えば弁別反応時間には、刺激の弁別だけでなく、反応するかしないか(Go/No-Go)という反応選択処理が含まれているとも考えられる。 | |||
このため、反応時間の差の絶対的な値に意味を見出すのは難しい。 | |||
とは言え、心的処理の速さへの関心は今なお続いている(近年では、特に物理的時間と心的時間のずれの問題として多くの研究者の興味を引いている | |||
<ref><pubmed>12200181</pubmed></ref><ref>'''ベンジャミン・リベット 下條信輔(訳)'''<br>マインド・タイム 脳と意識の時間<br>''東京: 岩波書店'': 2005</ref> | <ref><pubmed>12200181</pubmed></ref> | ||
<ref> | |||
'''ベンジャミン・リベット 下條信輔(訳)'''<br> | |||
マインド・タイム 脳と意識の時間<br> | |||
''東京: 岩波書店'': 2005 | |||
</ref> | |||
)。 | |||
減算法のアイデアの拡張・修正も提案されてきた | |||
<ref> | |||
'''S Sternberg'''<br> | |||
The discovery of processing stages: Extentions of Donders' method.<br> | |||
In W G Koster (ed), Attention and perfprmance II.<br> | |||
''Amsterdam: North-Holland'': 1969, pp. 276-315. | |||
</ref> | |||
<ref name=TeichnerKrebs1974><pubmed>4812881</pubmed></ref> | |||
。 | |||
現在では、反応時間のモデルは多くの変数を考慮に入れた複雑なものとなっている | |||
<ref name=MillerUlrich2003><pubmed>12643892</pubmed></ref> | |||
<ref name=RatcliffSmith2004><pubmed>15065913</pubmed></ref> | |||
。 | |||
==反応時間の性質== | ==反応時間の性質== | ||
| 83行目: | 160行目: | ||
===分布の非対称性=== | ===分布の非対称性=== | ||
[[ファイル:RTdistributions.png|thumb|320px|'''図2.''' | [[ファイル:RTdistributions.png|thumb|320px|'''図2.''' 反応時間の分布と変数変換。 | ||
1名の被験者による視覚選択反応時間(正答試行のみ)の分布の例。 | |||
中段は同じデータを対数変換したもの、下段は逆数変換したものを示す。 | |||
変数変換により、分布の非対称性が減じている。 | |||
]] | |||
反応時間の分布は正の歪度を示す非対称形になる(図2)。 | |||
反応の速さには限界がある一方、非常に遅い反応も一定数生じるためである。 | |||
歪度の大きさは実験内容に大きく依存し、指数分布様の極めて非対称な場合から正規分布様のほぼ対称な場合まで様々である。 | |||
分析に際しては、この非対称性に留意する必要がある。 | |||
反応時間分布にあてはめるモデルとしては、 | |||
[[wikipedia:Exponentially_modified_Gaussian_distribution|ex-Gaussian分布]] を用いることが多い<ref name=Ratcliff1993><pubmed>8272468</pubmed></ref><ref>'''T Van Zandt'''<br>Analysis of response time distributions.<br>In H Pashler, J Wixted (eds.) Steven's handbook of experimental psychology (3rd ed.) Volume 4, Methodology in experimental psychology.<br>''New York: John Wiley & Sons'': 2002, pp. 461-516.</ref> <ref>'''A Heathcote, S J Popiel, D J K Mewhort'''<br>Analysis of response time distributions: An example using the Stroop task.<br>''Psychol Bull'': 1993, 109;340-347 </ref> <ref>'''Y Lacouture, D Cousineau'''<br>How to use MATLAB to fit the ex-Gaussian and other probability functions to a distribution of response times.<br> | [[wikipedia:ja:ワイブル分布|ワイブル分布]]や[[wikipedia:ja:対数正規分布|対数正規分布]]も用いるが、 | ||
''Tutorials in Quantitative Methods for Psychology'': 2008, 4;35-45 </ref>。 | [[wikipedia:Exponentially_modified_Gaussian_distribution|ex-Gaussian分布]] を用いることが多い | ||
<ref name=Ratcliff1993><pubmed>8272468</pubmed></ref> | |||
<ref> | |||
'''T Van Zandt'''<br> | |||
Analysis of response time distributions.<br> | |||
In H Pashler, J Wixted (eds.) Steven's handbook of experimental psychology (3rd ed.) Volume 4, Methodology in experimental psychology.<br> | |||
''New York: John Wiley & Sons'': 2002, pp. 461-516. | |||
</ref> | |||
<ref> | |||
'''A Heathcote, S J Popiel, D J K Mewhort'''<br> | |||
Analysis of response time distributions: An example using the Stroop task.<br> | |||
''Psychol Bull'': 1993, 109;340-347 | |||
</ref> | |||
<ref> | |||
'''Y Lacouture, D Cousineau'''<br> | |||
How to use MATLAB to fit the ex-Gaussian and other probability functions to a distribution of response times.<br> | |||
''Tutorials in Quantitative Methods for Psychology'': 2008, 4;35-45 | |||
</ref> | |||
。 | |||
===速さと正確さのトレードオフ=== | ===速さと正確さのトレードオフ=== | ||
反応は速くしようとするほど不正確になり、正確にしようとするほど遅くなる。 | |||
この交換関係を速さと正確さのトレードオフ(speed-accuracy tradeoff, SAT)という。 | |||
平均選択反応時間 <math>RT</math> と正答率 <math>P(C)</math> ・誤答率 <math>P(E)</math> の関係は次式で記述できる | |||
(<math>a</math>, <math>b</math> はパラメータ) | |||
<ref name=Welford1980ch3> | |||
'''A T Welford'''<br> | |||
Choice reaction time: Basic concepts.<br> | |||
In A T Welford (ed.) Reaction times. | |||
''London: Academic Press'': 1980, pp. 73-128 | |||
</ref> | |||
。 | |||
<math>RT = a + b \log \frac{P(C)}{P(E)} \, </math> | |||
従って、反応時間を分析する際は、正答率・誤答率など正確さの指標もあわせて考慮する必要がある。 | |||
また、速さと正確さのトレードオフが適切に制御された実験を計画することが重要である。 | |||
例えば、反応時間は条件1の方が短いが、誤答率は条件2の方が低かったとすると、解釈が難しい。 | |||
この問題を避けるため、反応時間と正答率・誤答率のどちらかに目標を絞り込むことが多い。 | |||
トレードオフを制御する方法はいくつかある | |||
<ref name=Wickelgren1977> | |||
'''W A Wickelgren'''<br> | |||
Speed-accuracy tradeoff and information processing dynamics.<br> | |||
''Acta Psychol(Amst)'': 1977, 41;67-85 | |||
</ref>。 | |||
典型的には、教示と、課題難易度の調整を用いる。 | |||
正答率・誤答率を指標にしたい場合は、課題難易度をある程度難しくした上で、速さより正確さを優先するよう教示する。 | |||
逆に反応時間を指標にしたい場合は、時間をかければ誤答がほぼなくなるような難易度にし、できるだけ速くかつ正確に反応するよう教示する。 | |||
難易度は予備実験の結果を見て決定するが、全被験者一律にすることもあれば、被験者毎に決定することもある。 | |||
反応に時間制限を設けたり、決められた時(例えば音で知らされる)に必ず反応させることで反応時間を一定に制御する方法もある | |||
<ref name=SchoutenBekker1967><pubmed>6062205</pubmed></ref> | |||
。 | |||
===Hick-Hymanの法則=== | ===Hick-Hymanの法則=== | ||
平均選択反応時間 <math>RT</math> は、選択肢数 <math>n</math> が多いほど長い。Hick | |||
<ref name=Hick1952> | <ref name=Hick1952> | ||
'''W E Hick'''<br> | '''W E Hick'''<br> | ||
| 112行目: | 238行目: | ||
はこの関係が | はこの関係が | ||
<math>RT = K \log \left( n+1 \right) \, </math> | |||
という式で近似できることを発見した。これをHickの法則という。底に2をとれば | という式で近似できることを発見した。これをHickの法則という。底に2をとれば | ||
| 120行目: | 246行目: | ||
、<math>K</math> は単純反応時間に相当する。なお、 | 、<math>K</math> は単純反応時間に相当する。なお、 | ||
<math>RT = a + b \log n \, </math> | |||
という式も同様によく用いられる | という式も同様によく用いられる | ||
| 127行目: | 253行目: | ||
この場合、 <math>a</math> が単純反応時間に相当し、<math>b</math> はパラメータである。 | この場合、 <math>a</math> が単純反応時間に相当し、<math>b</math> はパラメータである。 | ||
さて、選択肢数が同じでも、出現確率の低い刺激に対する反応は遅い | |||
<ref name=Hyman1953><pubmed>13052851</pubmed></ref> | <ref name=Hyman1953><pubmed>13052851</pubmed></ref> | ||
<ref name=MillerPachella1973>'''J O Miller, R G Pachella'''<br>Locus of the stimulus probability effect.<br>''J Exp Psychol'': 1973, 101; 227-231 | <ref name=MillerPachella1973> | ||
'''J O Miller, R G Pachella'''<br> | |||
Locus of the stimulus probability effect.<br> | |||
''J Exp Psychol'': 1973, 101; 227-231 | |||
</ref> | </ref> | ||
。 | 。 | ||
この現象は、反応時間が刺激の情報量に比例すると解釈されている。 | |||
Hyman | Hyman | ||
<ref name=Hyman1953 /> | <ref name=Hyman1953 /> | ||
| 138行目: | 267行目: | ||
ことを示した。 | ことを示した。 | ||
<math>RT = a + b \log \left( \frac{1}{p} \right) \, </math> | |||
これをHick-Hymanの法則と言う。処理すべき情報量が多いほど反応に時間がかかるのである。 | |||
Hickの法則は、全選択肢が等確率( <math>p = 1/n</math> )のケースに相当する。 | |||
=== | ===先行期間(foreperiod, FP)=== | ||
典型的な実験では、まず予告刺激(warning signal) | |||
<ref>クリック音などの短時間の音刺激や、反応刺激出現位置を予告する小さな図形などが用いられる。 | <ref> | ||
クリック音などの短時間の音刺激や、反応刺激出現位置を予告する小さな図形などが用いられる。 | |||
反応刺激が視覚刺激の場合には、その出現時に被験者が別の場所を注視していると、刺激を見落としたり、 | 反応刺激が視覚刺激の場合には、その出現時に被験者が別の場所を注視していると、刺激を見落としたり、 | ||
反応刺激へ向かう眼球運動を生じて余計な時間がかかったりすることになる。 | 反応刺激へ向かう眼球運動を生じて余計な時間がかかったりすることになる。 | ||
そのため、十字などの注視点を予告刺激として提示し、これに必ず注視するよう被験者に求めることが多い。</ref> | そのため、十字などの注視点を予告刺激として提示し、これに必ず注視するよう被験者に求めることが多い。 | ||
</ref> | |||
を提示し、数秒程度の先行期間(foreperiod, FP)の後に反応すべき刺激(反応刺激、response stimulus)を提示する(図1) | を提示し、数秒程度の先行期間(foreperiod, FP)の後に反応すべき刺激(反応刺激、response stimulus)を提示する(図1) | ||
<ref name=ITI> | <ref name=ITI> | ||
被験者の反応から次の試行の予告刺激までの間、すなわち、試行と試行の間にも時間間隔がある。こちらはITI(inter-trial interval)と呼ばれる。通常、ITIは一定とする。</ref> | 被験者の反応から次の試行の予告刺激までの間、すなわち、試行と試行の間にも時間間隔がある。こちらはITI(inter-trial interval)と呼ばれる。通常、ITIは一定とする。 | ||
</ref> | |||
。被験者は予告刺激によって試行の開始を知り、反応に備える。 | 。被験者は予告刺激によって試行の開始を知り、反応に備える。 | ||
300msを下回るような極端に短いFPを用いると、反応が遅くなる。 | 300msを下回るような極端に短いFPを用いると、反応が遅くなる。 | ||
これは心理的不応期(psychological refractory period, PRP)と関連する現象と考えられている | |||
<ref name=Davis1959> | <ref name=Davis1959> | ||
'''R Davis'''<br> | '''R Davis'''<br> | ||
| 169行目: | 301行目: | ||
(ただし、<ref><pubmed>18255052</pubmed></ref>)。 | (ただし、<ref><pubmed>18255052</pubmed></ref>)。 | ||
FPの長さが常に一定だと、被験者は反応刺激の出現を予期できる。 | |||
これは特に単純反応時間の測定では問題になるので、FPを試行毎にランダムに変動させることがある。 | これは特に単純反応時間の測定では問題になるので、FPを試行毎にランダムに変動させることがある。 | ||
この場合、反応時間はFPが一定の場合より長くなる | この場合、反応時間はFPが一定の場合より長くなる | ||
| 192行目: | 324行目: | ||
===反応時間と神経活動=== | ===反応時間と神経活動=== | ||
反応が速い時には、中枢神経系でも情報処理が速く進行した可能性がある。 | |||
そこで、反応時間と神経活動の生理指標との関連性が、主に[[ | そこで、反応時間と神経活動の生理指標との関連性が、主に[[EEG]]のような時間解像度の高い方法で検討されてきた。 | ||
例えば視覚刺激の単純検出課題では、反応時間が長かった試行の視覚[[誘発電位]]は、反応時間が短かった試行に比べて、潜時が長く、また振幅も小さい | |||
<ref><pubmed>4160389</pubmed></ref> | <ref><pubmed>4160389</pubmed></ref> | ||
。 | 。 | ||
| 205行目: | 337行目: | ||
===刺激強度=== | ===刺激強度=== | ||
一般に、刺激強度(輝度や音圧)が強いほど単純反応時間は短い(光 | |||
<ref name=TeichnerKreb1974><pubmed>5038152</pubmed></ref> | <ref name=TeichnerKreb1974><pubmed>5038152</pubmed></ref> | ||
<ref name=Ueno1977><pubmed>867843</pubmed></ref> | <ref name=Ueno1977><pubmed>867843</pubmed></ref> | ||
| 214行目: | 346行目: | ||
''J Exp Psychol'': 1970, 84;383-391 | ''J Exp Psychol'': 1970, 84;383-391 | ||
</ref> | </ref> | ||
)。これは単に感覚器の応答が速くなるためだけでなく、いくつかの原因による | |||
<ref name=Nissen1977> | <ref name=Nissen1977> | ||
'''M J Nissen'''<br> | '''M J Nissen'''<br> | ||
| 220行目: | 352行目: | ||
''Percept Pstchophys'': 1977, 22;338-352 | ''Percept Pstchophys'': 1977, 22;338-352 | ||
</ref> | </ref> | ||
。刺激強度と反応時間の関係は、指数が負のべき関数で表せる(Piéronの法則 | |||
<ref name=PinsBonnet1996><pubmed>8935900</pubmed></ref> | <ref name=PinsBonnet1996><pubmed>8935900</pubmed></ref> | ||
)。 | )。 | ||
| 226行目: | 358行目: | ||
===刺激モダリティ=== | ===刺激モダリティ=== | ||
視覚刺激に対する単純反応時間は、聴覚刺激や触覚刺激に対するものより長い。味覚刺激や嗅覚刺激ではさらに長いと言われている | |||
<ref name=Welford1980ch1> | <ref name=Welford1980ch1> | ||
'''J M T Brebner, A T Welford'''<br> | '''J M T Brebner, A T Welford'''<br> | ||
| 239行目: | 371行目: | ||
</ref> | </ref> | ||
。 | 。 | ||
ただし、異なるモダリティの刺激の強度を何らかの意味で一致させた上での実験が必要なため | |||
(例えば光と音について | (例えば光と音について | ||
<ref name=Kohfeld1971><pubmed>5577177</pubmed></ref> | <ref name=Kohfeld1971><pubmed>5577177</pubmed></ref> | ||
)、厳密な比較は難しい。 | )、厳密な比較は難しい。 | ||
複数モダリティで同時に刺激が与えられる場合、つまり多感覚(multimodal)刺激の場合には、 | |||
単一モダリティ(unimodal)刺激の場合に比べて反応時間が短縮する | 単一モダリティ(unimodal)刺激の場合に比べて反応時間が短縮する | ||
<ref name=Nickerson1973><pubmed>4757060</pubmed></ref> | <ref name=Nickerson1973><pubmed>4757060</pubmed></ref> | ||
。例えば、光刺激に対する単純反応時間は、音刺激が同時に提示されると短縮する。 | 。例えば、光刺激に対する単純反応時間は、音刺激が同時に提示されると短縮する。 | ||
このとき音刺激は課題に無関係でよく、これを付属刺激(accesory stimulus)と呼ぶ。 | |||
===反応方法=== | ===反応方法=== | ||
反応の動作を行う器官を効果器(effector)と呼ぶ。 | |||
効果器によって反応時間は異なる。 | |||
手指ボタン押しでは、ボタン上にあらかじめ指を乗せておき、指を動かすだけで反応できるようにする。 | |||
押していたボタンを離すことで反応させる方法もある。 | |||
手指ボタン押しに比べ、足でのペダル踏みや発声による口頭反応は数10ms遅い | |||
<ref name=Oyama1985 /> | <ref name=Oyama1985 /> | ||
<ref name=SeashoreSeashore1941> | <ref name=SeashoreSeashore1941> | ||
| 268行目: | 404行目: | ||
。 | 。 | ||
多数のボタンの一つを選んで押す課題では、腕を動かす必要がある。 | |||
このように大きな動作を伴う場合には、相応の運動時間(MT)が加わるので、 | |||
ボタン押し反応時間は手指ボタン押しの場合より長くなる(図1)。 | ボタン押し反応時間は手指ボタン押しの場合より長くなる(図1)。 | ||
===左右差=== | ===左右差=== | ||
単純反応時間では、右手・足による反応と左手・足による反応で差はない | |||
<ref name=SeashoreSeashore1941 /> | <ref name=SeashoreSeashore1941 /> | ||
<ref name=Oyama1985 /> | <ref name=Oyama1985 /> | ||
<ref name=Simon1967><pubmed>6065838</pubmed></ref>。 | <ref name=Simon1967><pubmed>6065838</pubmed></ref> | ||
。 | |||
選択反応時間では、利き手の反応の方が速いことがある | |||
<ref name=Rabbitt1978><pubmed>693786</pubmed></ref> | <ref name=Rabbitt1978><pubmed>693786</pubmed></ref> | ||
<ref name=KerrEtal1963><pubmed>14079023</pubmed></ref>。 | <ref name=KerrEtal1963><pubmed>14079023</pubmed></ref> | ||
。 | |||
一般に利き手は非利き手より運動に関わる成績がよく、運動時間(MT)や運動の正確さで利き手の優位性が見られる | 一般に利き手は非利き手より運動に関わる成績がよく、運動時間(MT)や運動の正確さで利き手の優位性が見られる | ||
<ref name=ElliottEtal1993>'''D Elliott, E A Roy, D Goodman, R G Carson, R Chua, B K V Maraj'''<br> | <ref name=ElliottEtal1993> | ||
Asymmetries in the preparation and control of manual aiming movements.<br>''Can J Exp Psychol'': 1993, 47;570-589</ref>。 | '''D Elliott, E A Roy, D Goodman, R G Carson, R Chua, B K V Maraj'''<br> | ||
Asymmetries in the preparation and control of manual aiming movements.<br> | |||
<ref name=CarsonEtal1990><pubmed>2290495</pubmed></ref>。 | ''Can J Exp Psychol'': 1993, 47;570-589 | ||
</ref> | |||
また、個人差も大きい<ref name=AnnettAnnett1979><pubmed>486877</pubmed></ref>。 | 。 | ||
ところが、視覚標的への指差し反応ではむしろ非利き手の方がMTを除いた反応時間(刺激提示から運動開始までの時間)が短い | |||
<ref name=CarsonEtal1990><pubmed>2290495</pubmed></ref> | |||
。 | |||
これは空間情報処理の大脳右半球優位性のためと考えられている。 | |||
反応時間の左右差は知覚から運動まで様々な段階の左右差を反映するため、課題内容によっても結果が変化する | |||
<ref name=Rabbitt1978 /> | |||
<ref name=ElliottEtal1993 /> | |||
。 | |||
また、個人差も大きい | |||
<ref name=AnnettAnnett1979><pubmed>486877</pubmed></ref> | |||
。 | |||
感覚器官の左右差が見られることもある。 | |||
視覚単純反応時間も、刺激を利き目に提示した方が短くなる<ref name=MunicciConnors1964><pubmed>14129728</pubmed></ref>。 | 聴覚単純反応時間は、刺激が右耳に提示された時の方がわずかに短い | ||
なお、単眼提示より両眼提示<ref name=MunicciConnors1964 />、また片耳提示より両耳提示<ref name=Simon1967 />の方が反応時間は短い。 | <ref name=Simon1967 /> | ||
。 | |||
視覚単純反応時間も、刺激を利き目に提示した方が短くなる | |||
<ref name=MunicciConnors1964><pubmed>14129728</pubmed></ref> | |||
。 | |||
なお、単眼提示より両眼提示 | |||
<ref name=MunicciConnors1964 /> | |||
、また片耳提示より両耳提示 | |||
<ref name=Simon1967 /> | |||
の方が反応時間は短い。 | |||
===刺激-反応適合性=== | ===刺激-反応適合性=== | ||
| 296行目: | 455行目: | ||
[[ファイル:RTcompatibility.png|frame|'''図3.''' 空間的刺激-反応適合性(spatial S-R compatibility)の例。 | [[ファイル:RTcompatibility.png|frame|'''図3.''' 空間的刺激-反応適合性(spatial S-R compatibility)の例。 | ||
右のランプが点灯したら右のボタンを押す場合(適合条件)では、右のランプが点灯したら左のボタンを押す場合(非適合条件) | 右のランプが点灯したら右のボタンを押す場合(適合条件)では、右のランプが点灯したら左のボタンを押す場合(非適合条件) | ||
よりも、反応時間が短くなる。]] | よりも、反応時間が短くなる。 | ||
]] | |||
刺激の特性と反応の特性が適合的なときは、非適合的なときより反応が速く正確になる。 | |||
例えば高い音に対して「高い」、低い音に対して「低い」と答えるのは、 | |||
高い音に対して「低い」、低い音に対して「高い」と答えるより容易である。 | |||
このような違いを、刺激-反応適合性(stimulus-response compatibility)の効果と呼ぶ | |||
<ref name=FittsSeeger1953><pubmed>13084867</pubmed></ref> | |||
<ref name=ProctorReeve1990> | <ref name=ProctorReeve1990> | ||
'''R W Proctor, T G Reeve (eds.)'''<br> | '''R W Proctor, T G Reeve (eds.)'''<br> | ||
Stimulus-response compatibility: An integrated perspective.<br> | Stimulus-response compatibility: An integrated perspective.<br> | ||
''Amsterdam: North-Holland'': 1990</ref>。 | ''Amsterdam: North-Holland'': 1990 | ||
</ref> | |||
。 | |||
よく研究されているのは空間的適合性である(図3)。 | |||
、聴覚<ref name=SimonEtal1970><pubmed>5482039</pubmed></ref> | 例えば右側の刺激に対しては右のボタンで、左の刺激に対しては左のボタンで反応する方が、その逆の組合せよりも速い。 | ||
、触覚<ref name=Peters1983><pubmed>6571317</pubmed></ref> | これは視覚 | ||
<ref name=FittsSeeger1953 /> | |||
<ref name=Wallace1971><pubmed>5090926</pubmed></ref> | |||
、聴覚 | |||
<ref name=SimonEtal1970><pubmed>5482039</pubmed></ref> | |||
、触覚 | |||
<ref name=Peters1983><pubmed>6571317</pubmed></ref> | |||
のいずれでも起こる。 | |||
両手を交差させ右(左)手で左(右)のボタンを押す場合や | |||
<ref name=Wallace1971 /> | |||
、両手(交差させない)でそれぞれ棒を持ち棒を交差させ右(左)手の棒で左(右)のボタンを押す場合でも | 、両手(交差させない)でそれぞれ棒を持ち棒を交差させ右(左)手の棒で左(右)のボタンを押す場合でも | ||
<ref name=RiggioEtal1986> | <ref name=RiggioEtal1986> | ||
'''L Riggio, L de G Gawryszewski, C Umiltà'''<br> | '''L Riggio, L de G Gawryszewski, C Umiltà'''<br> | ||
What is crossed in crossed-hand effects?<br> | What is crossed in crossed-hand effects?<br> | ||
''Acta Psychol (Amst)'': 1986, 62;89-100</ref>、刺激位置とボタン位置との間の空間適合性に従った効果が見られる。 | ''Acta Psychol (Amst)'': 1986, 62;89-100 | ||
</ref> | |||
、刺激位置とボタン位置との間の空間適合性に従った効果が見られる。 | |||
===疲労と学習=== | ===疲労と学習=== | ||
実験では、被験者は同じ課題を長時間にわたり繰り返す。 | |||
このとき、単純反応時間はビジランス(vigilance, 持続的[[注意]])の低下や疲労により次第に長くなる | |||
<ref name=Buck1966><pubmed>5325893</pubmed></ref> | <ref name=Buck1966><pubmed>5325893</pubmed></ref> | ||
<ref name=LangnerEtal2010><pubmed>20146071</pubmed></ref> | <ref name=LangnerEtal2010><pubmed>20146071</pubmed></ref> | ||
| 331行目: | 507行目: | ||
。 | 。 | ||
一方、選択反応時間は学習効果により短くなることも報告されている。 | |||
特に選択肢数が多いと効果が大きいようだが、2肢でも効果は見られる | 特に選択肢数が多いと効果が大きいようだが、2肢でも効果は見られる | ||
<ref name=Welford1980ch3 /> | <ref name=Welford1980ch3 /> | ||
| 337行目: | 513行目: | ||
。 | 。 | ||
十分な練習や休憩により、実験中の反応時間を安定させることができる。 | |||
===年齢=== | ===年齢=== | ||
多くの課題で、反応時間は20代に最も短くなる | |||
<ref name=Welford1980ch9 /> | <ref name=Welford1980ch9 /> | ||
<ref name=WilliamsEtal2005><pubmed>15656766</pubmed></ref> | <ref name=WilliamsEtal2005><pubmed>15656766</pubmed></ref> | ||
| 349行目: | 525行目: | ||
。 | 。 | ||
成人では[[加齢]]に従って反応時間が伸びる。 | |||
種々の課題で高齢者の反応時間は若齢者より長い | 種々の課題で高齢者の反応時間は若齢者より長い | ||
<ref name=Cerella1985><pubmed>4034819</pubmed></ref> | <ref name=Cerella1985><pubmed>4034819</pubmed></ref> | ||
| 362行目: | 538行目: | ||
</ref> | </ref> | ||
。 | 。 | ||
単純反応時間も[[加齢]]に伴い長くなるが、その程度は緩やかで、しばしば高齢者と若齢者で差が見られない | |||
<ref name=FozardEtal1994 /> | <ref name=FozardEtal1994 /> | ||
<ref name=AnsteyEtal2005 /> | <ref name=AnsteyEtal2005 /> | ||
| 375行目: | 551行目: | ||
===性別=== | ===性別=== | ||
男性より女性の方が平均して反応時間は長く、単純反応時間で数10msの差が見られる | |||
<ref name=SeashoreSeashore1941 /> | <ref name=SeashoreSeashore1941 /> | ||
<ref name=Welford1980ch9 /> | <ref name=Welford1980ch9 /> | ||
。 | 。 | ||
同様の[[ | 同様の[[性差]]は高齢者でも | ||
<ref name=FozardEtal1994 /> | <ref name=FozardEtal1994 /> | ||
<ref name=DerDeary2006 /> | <ref name=DerDeary2006 /> | ||
| 393行目: | 569行目: | ||
===薬物=== | ===薬物=== | ||
[[カフェイン]]や[[ニコチン]]はしばしば選択反応時間を短縮する | |||
。[[ | <ref name=LiebermanEtal1987><pubmed>3114783</pubmed></ref> | ||
<ref name=KerrEtal1991><pubmed>1881996</pubmed></ref> | |||
<ref name=HindmarchEtal1990><pubmed>2320715</pubmed></ref> | |||
。[[アルコール]]や | |||
<ref name=KerrEtal1991 /> | |||
<ref name=MaylorRabbitt1993><pubmed>8401986</pubmed></ref> | |||
<ref> | |||
'''倪 臻、笠井達哉、長谷川善輝、林 司佳子、矢作 晋'''<br> | '''倪 臻、笠井達哉、長谷川善輝、林 司佳子、矢作 晋'''<br> | ||
アルコール摂取がヒトの反応時間及び運動野の抑制回路に及ぼす影響<br> | アルコール摂取がヒトの反応時間及び運動野の抑制回路に及ぼす影響<br> | ||
''日本運動生理学雑誌'': 2003, 10;55-63 | ''日本運動生理学雑誌'': 2003, 10;55-63 | ||
</ref> | </ref> | ||
[[ベンゾジアゼピン]]は | |||
<ref name=DawsonEtal2008><pubmed>18570226</pubmed></ref> | |||
単純反応時間や選択反応時間を長くする。 | 単純反応時間や選択反応時間を長くする。 | ||
===その他=== | ===その他=== | ||
刺激の特性では、強度以外にも提示時間 | |||
<ref name=UlrichEtal1998><pubmed>9627425</pubmed></ref> | <ref name=UlrichEtal1998><pubmed>9627425</pubmed></ref> | ||
<ref name=Raab1962><pubmed>14489536</pubmed></ref> | <ref name=Raab1962><pubmed>14489536</pubmed></ref> | ||
、視覚刺激の[[網膜]]位置 | 、視覚刺激の[[網膜]]位置 | ||
<ref name=Rains1962><pubmed>14168292</pubmed></ref> | <ref name=Rains1962><pubmed>14168292</pubmed></ref> | ||
、空間周波数 | |||
<ref name=LuppEtal1976><pubmed>948887</pubmed></ref> | <ref name=LuppEtal1976><pubmed>948887</pubmed></ref> | ||
、コントラスト | |||
<ref name=MillerPachella1973 /> | <ref name=MillerPachella1973 /> | ||
<ref name=LuppEtal1976 /> | <ref name=LuppEtal1976 /> | ||
| 427行目: | 610行目: | ||
==解釈の難しさ== | ==解釈の難しさ== | ||
反応時間は有用な指標だが、しばしばそのデータの解釈をめぐって論争がある | |||
しばしば議論となる。</ref>。 | <ref> | ||
例えば心的回転(mental rotation)で、図形の回転角度に比例した反応時間は、 | |||
心的イメージが刺激のアナログ的な表象である証拠と解釈された。 | |||
しかしこの解釈には反論が多く、心理学上の論争となった(イメージ論争)。 | |||
また視覚探索(visual search, 例えば画面上の10個の物体の中から目的の物体を探し出す課題)では、 | |||
反応時間が物体数に比例して長くなることがあるが、 | |||
これが逐次的情報処理(物体を1つずつ処理する)の反映なのか、 | |||
並列的情報処理(複数物体を同時に処理する)の速さが変化することの反映なのか、 | |||
しばしば議論となる。 | |||
</ref> | |||
。 | |||
反応方法や計測方法の違いで変化してしまうことからもわかるように、心的処理について考える上で反応時間の絶対的な値には意味がないことが多い。 | 反応方法や計測方法の違いで変化してしまうことからもわかるように、心的処理について考える上で反応時間の絶対的な値には意味がないことが多い。 | ||
今日ほとんどの研究では、条件間で反応時間に相対的な差があるかどうかを検討している。 | 今日ほとんどの研究では、条件間で反応時間に相対的な差があるかどうかを検討している。 | ||
また、反応時間に影響した要因は刺激の知覚から運動まであらゆる段階に求められるので、正確な特定は難しいことが多い。 | |||
例えば単純反応時間は平均的には男性の方が女性より短い | 例えば単純反応時間は平均的には男性の方が女性より短い | ||
<ref name=SeashoreSeashore1941 /> | <ref name=SeashoreSeashore1941 /> | ||
| 450行目: | 643行目: | ||
==測定と分析の実際== | ==測定と分析の実際== | ||
[[ファイル:RTresponseboxes.jpg|thumb | [[ファイル:RTresponseboxes.jpg|thumb|'''図4.''' 実験用反応ボタンの例]] | ||
===器具=== | ===器具=== | ||
かつて反応時間測定には電鍵やクロノスコープ | |||
<ref> | <ref> | ||
英:chronoscope 機械式の精密な計時装置。下記文献等を参照。<br> | 英:chronoscope 機械式の精密な計時装置。下記文献等を参照。<br> | ||
| 466行目: | 659行目: | ||
高い精度が求められる実験では、専用の反応装置(図4)と刺激提示装置が用いられる。 | 高い精度が求められる実験では、専用の反応装置(図4)と刺激提示装置が用いられる。 | ||
口頭反応では、音圧が最初のピークか一定の閾値(例えば、ピーク音圧の10%や50%)に達した時を反応とする。 | |||
垂直跳びによる全身反応時間の測定では、スイッチを踏ませておき、両足がスイッチを離れたことで反応とする。 | 垂直跳びによる全身反応時間の測定では、スイッチを踏ませておき、両足がスイッチを離れたことで反応とする。 | ||
モーションキャプチャや高速度ビデオ撮影も有効である。 | モーションキャプチャや高速度ビデオ撮影も有効である。 | ||
いずれの方法でも、刺激提示装置と反応記録装置の時間的な同期を正確にとることが肝要である | |||
<ref> | <ref> | ||
特に、視覚刺激を一般的なディスプレイ装置で提示する場合には、時間解像度があまり高くないことに留意する必要がある。 | 特に、視覚刺激を一般的なディスプレイ装置で提示する場合には、時間解像度があまり高くないことに留意する必要がある。 | ||
例えばリフレッシュレートが60Hzならば、視覚刺激は16.7 msの単位でしか操作できない。 | 例えばリフレッシュレートが60Hzならば、視覚刺激は16.7 msの単位でしか操作できない。 | ||
精密な実験では、フォトダイオードなどを用いて実際に画面が刺激光を発する時間を確かめるべきである。 | 精密な実験では、フォトダイオードなどを用いて実際に画面が刺激光を発する時間を確かめるべきである。 | ||
</ref>。 | </ref> | ||
。 | |||
===誤答の除外=== | ===誤答の除外=== | ||
研究目的にもよるが、誤答の反応時間は分析から除外するのが一般的である。 | |||
ただし、誤答が少なくない時には誤答反応時間の分析が役立つこともある(例えば<ref><pubmed>15917795</pubmed></ref>)。 | 課題がきちんと遂行されなかったと考えられるからである。 | ||
ただし、誤答が少なくない時には誤答反応時間の分析が役立つこともある(例えば | |||
<ref><pubmed>15917795</pubmed></ref> | |||
)。 | |||
===分布の非対称性と外れ値への対処=== | ===分布の非対称性と外れ値への対処=== | ||
反応時間は分布が非対称になりやすく、また外れ値(outlier)を含む。 | |||
従って、算術平均を代表値としたり、分散分析のような正規性を仮定する分析を適用することには問題が多い。 | |||
まずデータの分布を見て、強い非対称性や明らかな外れ値がないか確認すべきである。 | |||
算術平均のかわりに、よく中央値が用いられる。外れ値の除外(cutoff)および変数変換も有効である | |||
<ref name=Ratcliff1993 /> | |||
。 | |||
変数変換には、対数変換や逆数変換が用いられる(図2)。 | |||
反応時間の逆数は反応速度の指標とみなすことができる。 | |||
外れ値は一定の基準に基づいて除外する。 | |||
平均からの一定距離を基準とする(例えば、平均±3標準偏差を超えたら除外)のは、分布の非対称性を考えれば妥当ではない。 | |||
適切な変数変換の後に行うべきである。 | |||
上限と下限を一律に定めて除外する方法もある。 | |||
単純反応時間は平均150~300ms程度なので、これを極端に下回る反応時間は尚早反応、つまりフライングの結果である可能性が高い。 | |||
そこで、100ないし150ms程度を下限とし、それ以下は外れ値と見なす。 | |||
上限の基準はしばしば恣意的だが、概して除外されるデータが全体の数%以下になる程度に決められるようである。 | 上限の基準はしばしば恣意的だが、概して除外されるデータが全体の数%以下になる程度に決められるようである。 | ||
| 494行目: | 702行目: | ||
<references/> | <references/> | ||
(執筆者:新美亮輔・横澤一彦、担当編集委員:) | |||
2012年3月29日 (木) 12:28時点における版
英:reaction time/response time、英略語:RT
同義語:反応潜時
反応時間とは、生体に刺激が与えられてからその刺激に対する外的に観察可能な反応が生じるまでの時間である。 特に、ヒトが何らかの知覚・認知課題を遂行する際の、随意的行動による反応について言う(例えば、ランプが点灯したらすぐボタンを押す)。 類義語に潜時(latency)があるが、これは反応時間より広い概念で、ヒト以外の動物の反応や、 行動ではなく生理指標として観察される反応についても言う(例えば、視覚刺激提示から視覚誘発電位が生じるまでの時間)。 ここでは、ヒトの行動実験における反応時間について概説する。
反応時間は課題遂行成績(performance)の重要な指標である。 反応時間が長いほど、複雑で多くの心的処理を要したと考えられる。 ただし、反応時間は刺激の入力から反応の出力までに起こる種々の処理過程を総体として反映する指標である。 それらは少なくとも刺激の知覚、判断や反応選択、反応のための運動実行の3つに分けられるが、いずれの処理段階も反応時間に影響を生じうる。 なお、反応時間の平均的な長さだけでなく、ばらつき(標準偏差など)が分析されることもある。
いろいろな反応時間
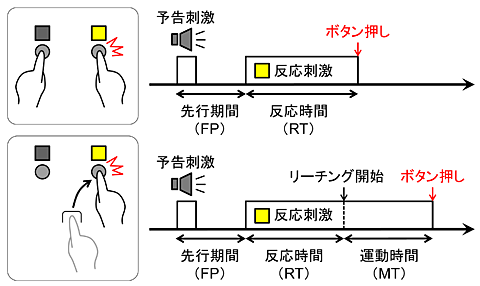
反応時間測定では、手指ボタン押し反応のほか、 足のペダル押し、発声、眼球運動なども用いられる [1] 。 リーチング [2] のような動作に比較的時間のかかる反応では、刺激提示から運動開始までを反応時間、 運動開始から終了までを運動時間(movement time, MT)と呼んで区別することもある(図1)。 短距離走のスタートのような全身運動による反応については、全身反応時間(whole body reaction time)と呼ぶ。 例えば、刺激が提示されたらできるだけ速く跳び上がらせ(垂直跳び課題)、両足が地を離れるまでの時間として測定する。
ただし、単純な反応動作でも多数の筋肉が関与するものである。 EMGで筋肉の運動潜時を調べると、反応時間と一致するとは限らないし、筋によっても差がある [3]。
課題による分類
一般に反応時間測定では、できるだけ速く反応する課題(speeded task)を用いる。 これに対し、好きな時に反応してよい課題の反応時間は自由反応時間(free reaction time)と呼んで区別することがある。 また、課題の内容に応じて、次の3種類が区別される。
単純反応時間(simple reaction time, SRT)[4]
既知の1種の刺激が提示され、それに対して決められた1種の反応をする(単純検出課題)ときの反応時間。 例えば、音が聞こえたらできるだけ速くボタンを押す。 下の2種よりも平均的には短く、視覚ないし聴覚刺激に対するボタン押しでは150~300ms程度である。
選択反応時間(choice reaction time, CRT)
既知の複数の刺激のいずれかが提示され、刺激に応じて決められた複数の反応のいずれかを行う (n肢強制選択課題; n-alternative forced choice task, nAFC task)ときの反応時間。 例えば、緑光か赤光が提示され、緑なら右、赤なら左のボタンをできるだけ速く押す(2肢強制選択課題; 2AFC task)。
Go/No-Go反応時間(Go/No-Go reaction time)
弁別反応時間(discriminative reaction time)とも。 既知の複数の刺激のいずれかが提示され、そのうち特定の刺激の場合のみ、決められた1種の反応をするときの反応時間。 例えば、緑光か赤光が提示され、緑ならボタンを押し、赤なら何もしない。 つまり、反応するかしないか(Go/No-Go)を判断する。
初期の研究
神経伝達速度の測定
反応時間測定は19世紀末の実験心理学成立当初から行われている。 現在では反応時間は研究の手段として用いられることが多いが、当時は反応時間自体が研究対象だった。 生理学者や心理学者が、心的処理の速さはどれくらいかを測ろうとしたのである。 19世紀末は心的時間測定(mental chronometry)の時代であった [5] 。
直接の契機は、1849~1850年にヘルムホルツが カエル運動神経伝達速度を毎秒24.6~35.4mと測定したことだった [6] [7] [8] 。 私たちは日常的には、自分が意図した瞬間に体が動き、心的処理は「瞬時に」完了すると思っている。 これに反して神経の働きは意外に遅く、十分測定可能な程度の速さでしかなかったのである。
ドンデルスの減算法
では、知覚や判断はどれくらいの速さなのだろうか。 ヒトでの反応時間研究の嚆矢はオランダのドンデルスらによる1860年代の実験 [9] [10] とされる。 彼らは、反応時間のうち本当に心的処理(mental process)に要した時間を測ろうとした。 例えば、緑光に対して右、赤光に対して左のボタンを押す課題で、反応時間が仮に300msだとしても、色弁別の心的処理に300msかかるとは言えない。 そのうち相応の部分は、網膜から脳への伝達時間や脳から手の筋肉への伝達時間のはずだからである。
ドンデルスらは、減算法(subtraction method)と呼ばれる方法でこの問題に取り組んだ。 音声を聞いたらできるだけ速く発声して反応するという課題を使い、以下の反応時間を測定した。
- 単純反応時間。kiに対して、できるだけ速くkiと発声して反応する。
- 選択反応時間。ka, ke, ki, ko, kuのいずれかが提示され、できるだけ速く刺激と同じ音声を発して反応する。
- 弁別反応時間。ka, ke, ki, ko, kuのいずれかが提示され、kiの場合のみkiと発声して反応する。
結果は、順に平均201ms、284ms、237msとなった[10]。 選択反応時間から単純反応時間を引いた差83msは、刺激の弁別と反応の選択の心的処理に要した時間と考えられる。 選択反応時間から弁別反応時間を引いた差47msは、反応の選択の心的処理に要した時間と考えられる (弁別課題では反応の選択は必要ないが、刺激の弁別は必要である)。 このように条件間の減算で心的処理に要する時間を推定するのが減算法である。
しかし、この試みはうまくいかなかった。 反応時間に影響を与える要因が多すぎるのである。個人差も大きい。 何より、知覚や認知といった心的処理を構成要素の単純な加算で考えることに限界があった。 今日よく知られているように神経系の情報処理は高度に並列的である。 また、用いた課題がどんな心的処理を含むのかについては解釈に幅がある。 例えば弁別反応時間には、刺激の弁別だけでなく、反応するかしないか(Go/No-Go)という反応選択処理が含まれているとも考えられる。 このため、反応時間の差の絶対的な値に意味を見出すのは難しい。
とは言え、心的処理の速さへの関心は今なお続いている(近年では、特に物理的時間と心的時間のずれの問題として多くの研究者の興味を引いている [11] [12] )。 減算法のアイデアの拡張・修正も提案されてきた [13] [14] 。 現在では、反応時間のモデルは多くの変数を考慮に入れた複雑なものとなっている [15] [16] 。
反応時間の性質
分布の非対称性
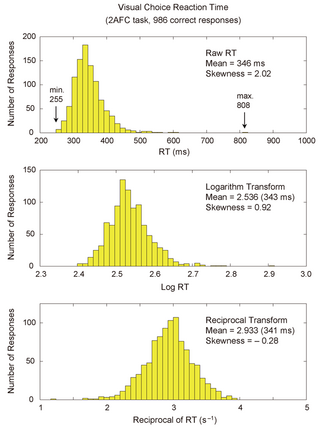
反応時間の分布は正の歪度を示す非対称形になる(図2)。 反応の速さには限界がある一方、非常に遅い反応も一定数生じるためである。 歪度の大きさは実験内容に大きく依存し、指数分布様の極めて非対称な場合から正規分布様のほぼ対称な場合まで様々である。 分析に際しては、この非対称性に留意する必要がある。
反応時間分布にあてはめるモデルとしては、 ワイブル分布や対数正規分布も用いるが、 ex-Gaussian分布 を用いることが多い [17] [18] [19] [20] 。
速さと正確さのトレードオフ
反応は速くしようとするほど不正確になり、正確にしようとするほど遅くなる。 この交換関係を速さと正確さのトレードオフ(speed-accuracy tradeoff, SAT)という。 平均選択反応時間 と正答率 ・誤答率 の関係は次式で記述できる (, はパラメータ) [21] 。
従って、反応時間を分析する際は、正答率・誤答率など正確さの指標もあわせて考慮する必要がある。 また、速さと正確さのトレードオフが適切に制御された実験を計画することが重要である。 例えば、反応時間は条件1の方が短いが、誤答率は条件2の方が低かったとすると、解釈が難しい。 この問題を避けるため、反応時間と正答率・誤答率のどちらかに目標を絞り込むことが多い。
トレードオフを制御する方法はいくつかある [22]。 典型的には、教示と、課題難易度の調整を用いる。 正答率・誤答率を指標にしたい場合は、課題難易度をある程度難しくした上で、速さより正確さを優先するよう教示する。 逆に反応時間を指標にしたい場合は、時間をかければ誤答がほぼなくなるような難易度にし、できるだけ速くかつ正確に反応するよう教示する。 難易度は予備実験の結果を見て決定するが、全被験者一律にすることもあれば、被験者毎に決定することもある。 反応に時間制限を設けたり、決められた時(例えば音で知らされる)に必ず反応させることで反応時間を一定に制御する方法もある [23] 。
Hick-Hymanの法則
平均選択反応時間 は、選択肢数 が多いほど長い。Hick [24] はこの関係が
という式で近似できることを発見した。これをHickの法則という。底に2をとれば [25] 、 は単純反応時間に相当する。なお、
という式も同様によく用いられる [21] 。 この場合、 が単純反応時間に相当し、 はパラメータである。
さて、選択肢数が同じでも、出現確率の低い刺激に対する反応は遅い [26] [27] 。 この現象は、反応時間が刺激の情報量に比例すると解釈されている。 Hyman [26] は、出現確率 の刺激に対する選択反応時間 は次式でよく記述できる ことを示した。
これをHick-Hymanの法則と言う。処理すべき情報量が多いほど反応に時間がかかるのである。 Hickの法則は、全選択肢が等確率( )のケースに相当する。
先行期間(foreperiod, FP)
典型的な実験では、まず予告刺激(warning signal) [28] を提示し、数秒程度の先行期間(foreperiod, FP)の後に反応すべき刺激(反応刺激、response stimulus)を提示する(図1) [29] 。被験者は予告刺激によって試行の開始を知り、反応に備える。 300msを下回るような極端に短いFPを用いると、反応が遅くなる。 これは心理的不応期(psychological refractory period, PRP)と関連する現象と考えられている [30] [31] (ただし、[32])。
FPの長さが常に一定だと、被験者は反応刺激の出現を予期できる。 これは特に単純反応時間の測定では問題になるので、FPを試行毎にランダムに変動させることがある。 この場合、反応時間はFPが一定の場合より長くなる [33] [34] 。 FPが一定の場合には、FPが長いほど反応時間は長くなる [35] [34] [36] 。 これは長い時間を正確に予測するのが難しいためだと考えられる。 FPが変動する場合には、用いられるFPのうち短いFPで反応時間が長くなることがある [34] [37] 。 いずれにせよ、FPの操作は予期や構えに関係するため、その影響は複雑である。
反応時間と神経活動
反応が速い時には、中枢神経系でも情報処理が速く進行した可能性がある。 そこで、反応時間と神経活動の生理指標との関連性が、主にEEGのような時間解像度の高い方法で検討されてきた。 例えば視覚刺激の単純検出課題では、反応時間が長かった試行の視覚誘発電位は、反応時間が短かった試行に比べて、潜時が長く、また振幅も小さい [38] 。 近年ではfMRIでも類似の検討が試みられている [39] 。
反応時間に影響する要因
刺激強度
一般に、刺激強度(輝度や音圧)が強いほど単純反応時間は短い(光 [40] [41] 、音 [42] )。これは単に感覚器の応答が速くなるためだけでなく、いくつかの原因による [43] 。刺激強度と反応時間の関係は、指数が負のべき関数で表せる(Piéronの法則 [44] )。
刺激モダリティ
視覚刺激に対する単純反応時間は、聴覚刺激や触覚刺激に対するものより長い。味覚刺激や嗅覚刺激ではさらに長いと言われている [45] [46] 。 ただし、異なるモダリティの刺激の強度を何らかの意味で一致させた上での実験が必要なため (例えば光と音について [47] )、厳密な比較は難しい。
複数モダリティで同時に刺激が与えられる場合、つまり多感覚(multimodal)刺激の場合には、 単一モダリティ(unimodal)刺激の場合に比べて反応時間が短縮する [48] 。例えば、光刺激に対する単純反応時間は、音刺激が同時に提示されると短縮する。 このとき音刺激は課題に無関係でよく、これを付属刺激(accesory stimulus)と呼ぶ。
反応方法
反応の動作を行う器官を効果器(effector)と呼ぶ。 効果器によって反応時間は異なる。 手指ボタン押しでは、ボタン上にあらかじめ指を乗せておき、指を動かすだけで反応できるようにする。 押していたボタンを離すことで反応させる方法もある。 手指ボタン押しに比べ、足でのペダル踏みや発声による口頭反応は数10ms遅い [46] [49] 。垂直跳びによる全身反応時間はさらに長く、視覚または聴覚刺激に対する単純反応時間で300~400ms程度である [50] 。
多数のボタンの一つを選んで押す課題では、腕を動かす必要がある。 このように大きな動作を伴う場合には、相応の運動時間(MT)が加わるので、 ボタン押し反応時間は手指ボタン押しの場合より長くなる(図1)。
左右差
単純反応時間では、右手・足による反応と左手・足による反応で差はない [49] [46] [51] 。 選択反応時間では、利き手の反応の方が速いことがある [52] [53] 。 一般に利き手は非利き手より運動に関わる成績がよく、運動時間(MT)や運動の正確さで利き手の優位性が見られる [54] 。 ところが、視覚標的への指差し反応ではむしろ非利き手の方がMTを除いた反応時間(刺激提示から運動開始までの時間)が短い [55] 。 これは空間情報処理の大脳右半球優位性のためと考えられている。 反応時間の左右差は知覚から運動まで様々な段階の左右差を反映するため、課題内容によっても結果が変化する [52] [54] 。 また、個人差も大きい [56] 。
感覚器官の左右差が見られることもある。 聴覚単純反応時間は、刺激が右耳に提示された時の方がわずかに短い [51] 。 視覚単純反応時間も、刺激を利き目に提示した方が短くなる [57] 。 なお、単眼提示より両眼提示 [57] 、また片耳提示より両耳提示 [51] の方が反応時間は短い。
刺激-反応適合性
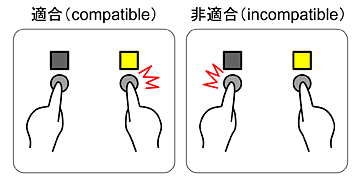
刺激の特性と反応の特性が適合的なときは、非適合的なときより反応が速く正確になる。 例えば高い音に対して「高い」、低い音に対して「低い」と答えるのは、 高い音に対して「低い」、低い音に対して「高い」と答えるより容易である。 このような違いを、刺激-反応適合性(stimulus-response compatibility)の効果と呼ぶ [58] [59] 。
よく研究されているのは空間的適合性である(図3)。 例えば右側の刺激に対しては右のボタンで、左の刺激に対しては左のボタンで反応する方が、その逆の組合せよりも速い。 これは視覚 [58] [60] 、聴覚 [61] 、触覚 [62] のいずれでも起こる。 両手を交差させ右(左)手で左(右)のボタンを押す場合や [60] 、両手(交差させない)でそれぞれ棒を持ち棒を交差させ右(左)手の棒で左(右)のボタンを押す場合でも [63] 、刺激位置とボタン位置との間の空間適合性に従った効果が見られる。
疲労と学習
実験では、被験者は同じ課題を長時間にわたり繰り返す。 このとき、単純反応時間はビジランス(vigilance, 持続的注意)の低下や疲労により次第に長くなる [64] [65] 。 このため、単純検出課題はビジランスの測定に用いられる。 選択反応時間も疲労により長くなる [66] 。
一方、選択反応時間は学習効果により短くなることも報告されている。 特に選択肢数が多いと効果が大きいようだが、2肢でも効果は見られる [21] [67] 。
十分な練習や休憩により、実験中の反応時間を安定させることができる。
年齢
多くの課題で、反応時間は20代に最も短くなる [66] [68] 。 児童では年齢とともに選択反応時間が短くなり、また個人内でのばらつきも減少するという [68] 。
成人では加齢に従って反応時間が伸びる。 種々の課題で高齢者の反応時間は若齢者より長い [69] 。 60代被験者の選択反応時間やGo/No-Go反応時間は、20代被験者に比べ10~30%程度長くなるようである [70] [71] [72] 。 単純反応時間も加齢に伴い長くなるが、その程度は緩やかで、しばしば高齢者と若齢者で差が見られない [70] [71] [72] 。 なお、高齢者では反応時間の個人内でのばらつきも増加する [68] [71] [73] 。
性別
男性より女性の方が平均して反応時間は長く、単純反応時間で数10msの差が見られる [49] [66] 。 同様の性差は高齢者でも [70] [73] 、 児童でも [74] 見られる。
薬物
カフェインやニコチンはしばしば選択反応時間を短縮する [75] [76] [77] 。アルコールや [76] [78] [79] ベンゾジアゼピンは [80] 単純反応時間や選択反応時間を長くする。
その他
刺激の特性では、強度以外にも提示時間 [81] [82] 、視覚刺激の網膜位置 [83] 、空間周波数 [84] 、コントラスト [27] [84] などが反応時間に影響する。 ストレス [66] や断眠 [85] 、一時的な運動 [86] 、スポーツの習熟 [87] などの効果も研究されている。
解釈の難しさ
反応時間は有用な指標だが、しばしばそのデータの解釈をめぐって論争がある [88] 。 反応方法や計測方法の違いで変化してしまうことからもわかるように、心的処理について考える上で反応時間の絶対的な値には意味がないことが多い。 今日ほとんどの研究では、条件間で反応時間に相対的な差があるかどうかを検討している。
また、反応時間に影響した要因は刺激の知覚から運動まであらゆる段階に求められるので、正確な特定は難しいことが多い。 例えば単純反応時間は平均的には男性の方が女性より短い [49] [66] が、これはただちに「男性は女性より速く刺激を知覚する」ということを意味しない。 男性は平均的に筋肉量が多く運動が速いのかも知れない(生理的要因)し、 男性は女性よりもスポーツをする機会が多いために感覚・運動協応機能が訓練されている者が多いのかも知れない [89] (社会的要因)。 こういった様々な要因を統制して実験を行うことが重要となる。 また、反応時間以外の測定値をあわせて用いることも有用である。
測定と分析の実際

器具
かつて反応時間測定には電鍵やクロノスコープ [90] が用いられた。 今日では、コンピュータのキーボードのキー押しを反応とし、コンピュータ内蔵のタイマーでその時間を測定することが多い。 簡単なプログラムや既成の実験用ソフトウェアによって測定できる。 高い精度が求められる実験では、専用の反応装置(図4)と刺激提示装置が用いられる。
口頭反応では、音圧が最初のピークか一定の閾値(例えば、ピーク音圧の10%や50%)に達した時を反応とする。 垂直跳びによる全身反応時間の測定では、スイッチを踏ませておき、両足がスイッチを離れたことで反応とする。 モーションキャプチャや高速度ビデオ撮影も有効である。
いずれの方法でも、刺激提示装置と反応記録装置の時間的な同期を正確にとることが肝要である [91] 。
誤答の除外
研究目的にもよるが、誤答の反応時間は分析から除外するのが一般的である。 課題がきちんと遂行されなかったと考えられるからである。 ただし、誤答が少なくない時には誤答反応時間の分析が役立つこともある(例えば [92] )。
分布の非対称性と外れ値への対処
反応時間は分布が非対称になりやすく、また外れ値(outlier)を含む。 従って、算術平均を代表値としたり、分散分析のような正規性を仮定する分析を適用することには問題が多い。 まずデータの分布を見て、強い非対称性や明らかな外れ値がないか確認すべきである。
算術平均のかわりに、よく中央値が用いられる。外れ値の除外(cutoff)および変数変換も有効である [17] 。 変数変換には、対数変換や逆数変換が用いられる(図2)。 反応時間の逆数は反応速度の指標とみなすことができる。
外れ値は一定の基準に基づいて除外する。 平均からの一定距離を基準とする(例えば、平均±3標準偏差を超えたら除外)のは、分布の非対称性を考えれば妥当ではない。 適切な変数変換の後に行うべきである。 上限と下限を一律に定めて除外する方法もある。 単純反応時間は平均150~300ms程度なので、これを極端に下回る反応時間は尚早反応、つまりフライングの結果である可能性が高い。 そこで、100ないし150ms程度を下限とし、それ以下は外れ値と見なす。 上限の基準はしばしば恣意的だが、概して除外されるデータが全体の数%以下になる程度に決められるようである。
参考文献・注
- ↑ 眼球運動の場合には反応時間ではなく潜時と呼ぶことが多い。
- ↑ 英:reaching、到達運動。目標となる物体に向けて手をのばす、あるいは手をのばして触れる行動。
- ↑
Moreno, M.A., Stepp, N., & Turvey, M.T. (2011).
Whole body lexical decision. Neuroscience letters, 490(2), 126-9. [PubMed:21184808] [PMC] [WorldCat] [DOI] - ↑ 古い文献では簡単反応時間と訳されることがある。
- ↑
E G Boring
A history of experimental psychology (2nd ed.)
New York: Appleton-Century-Crofts: 1950, p. 147 - ↑
K M Olesko, F L Holmes
Experiment, quantification, and discovery: Helmholtz's early physiological researches, 1843-50.
In David Cahan (ed), Hermann von Helmholtz and the foundations of nineteenth-century science.
Berkeley: University of California Press: 1993, pp. 50-108. - ↑
Finger, S., & Wade, N.J. (2002).
The neuroscience of Helmholtz and the theories of Johannes Müller. Part 1: Nerve cell structure, vitalism, and the nerve impulse. Journal of the history of the neurosciences, 11(2), 136-55. [PubMed:12122806] [WorldCat] [DOI] - ↑ 実際には、活動電位の伝達速度は髄鞘の有無や神経線維の太さによって大きく異なる。 ヒトの場合、遅いものでは毎秒0.5~2m、速いものでは最大毎秒75mに達する。
- ↑
J J de Jaager
Reaction time and mental processes.
In J Brozek, M S Sibinga (eds.), Origins of psychometry.
Nieuwkoop: B. de Graaf: 1970, pp. 33-73. - ↑ 10.0 10.1
Donders, F.C. (1969).
On the speed of mental processes. Acta psychologica, 30, 412-31. [PubMed:5811531] [WorldCat] [DOI] - ↑
Nijhawan, R. (2002).
Neural delays, visual motion and the flash-lag effect. Trends in cognitive sciences, 6(9), 387. [PubMed:12200181] [WorldCat] - ↑
ベンジャミン・リベット 下條信輔(訳)
マインド・タイム 脳と意識の時間
東京: 岩波書店: 2005 - ↑
S Sternberg
The discovery of processing stages: Extentions of Donders' method.
In W G Koster (ed), Attention and perfprmance II.
Amsterdam: North-Holland: 1969, pp. 276-315. - ↑
Teichner, W.H., & Krebs, M.J. (1974).
Laws of visual choice reaction time. Psychological review, 81(1), 75-98. [PubMed:4812881] [WorldCat] [DOI] - ↑
Miller, J., & Ulrich, R. (2003).
Simple reaction time and statistical facilitation: a parallel grains model. Cognitive psychology, 46(2), 101-51. [PubMed:12643892] [WorldCat] - ↑
Ratcliff, R., & Smith, P.L. (2004).
A comparison of sequential sampling models for two-choice reaction time. Psychological review, 111(2), 333-67. [PubMed:15065913] [PMC] [WorldCat] [DOI] - ↑ 17.0 17.1
Ratcliff, R. (1993).
Methods for dealing with reaction time outliers. Psychological bulletin, 114(3), 510-32. [PubMed:8272468] [WorldCat] [DOI] - ↑
T Van Zandt
Analysis of response time distributions.
In H Pashler, J Wixted (eds.) Steven's handbook of experimental psychology (3rd ed.) Volume 4, Methodology in experimental psychology.
New York: John Wiley & Sons: 2002, pp. 461-516. - ↑
A Heathcote, S J Popiel, D J K Mewhort
Analysis of response time distributions: An example using the Stroop task.
Psychol Bull: 1993, 109;340-347 - ↑
Y Lacouture, D Cousineau
How to use MATLAB to fit the ex-Gaussian and other probability functions to a distribution of response times.
Tutorials in Quantitative Methods for Psychology: 2008, 4;35-45 - ↑ 21.0 21.1 21.2
A T Welford
Choice reaction time: Basic concepts.
In A T Welford (ed.) Reaction times. London: Academic Press: 1980, pp. 73-128 - ↑
W A Wickelgren
Speed-accuracy tradeoff and information processing dynamics.
Acta Psychol(Amst): 1977, 41;67-85 - ↑
Schouten, J.F., & Bekker, J.A. (1967).
Reaction time and accuracy. Acta psychologica, 27, 143-53. [PubMed:6062205] [WorldCat] [DOI] - ↑
W E Hick
On the rate of gain of information.
Q J Exp Psychol: 1952, 4;11-26 - ↑ Hick-Hymanの法則では、情報量という観点から底に2をとることが多い。
- ↑ 26.0 26.1
HYMAN, R. (1953).
Stimulus information as a determinant of reaction time. Journal of experimental psychology, 45(3), 188-96. [PubMed:13052851] [WorldCat] [DOI] - ↑ 27.0 27.1
J O Miller, R G Pachella
Locus of the stimulus probability effect.
J Exp Psychol: 1973, 101; 227-231 - ↑ クリック音などの短時間の音刺激や、反応刺激出現位置を予告する小さな図形などが用いられる。 反応刺激が視覚刺激の場合には、その出現時に被験者が別の場所を注視していると、刺激を見落としたり、 反応刺激へ向かう眼球運動を生じて余計な時間がかかったりすることになる。 そのため、十字などの注視点を予告刺激として提示し、これに必ず注視するよう被験者に求めることが多い。
- ↑ 被験者の反応から次の試行の予告刺激までの間、すなわち、試行と試行の間にも時間間隔がある。こちらはITI(inter-trial interval)と呼ばれる。通常、ITIは一定とする。
- ↑
R Davis
The role of "attention" in the psychological refractory period.
Q J Exp Psyhol: 1959, 11:211-220 - ↑
A T Welford
The single-channel hypothesis.
In A T Welford (ed.) Reaction times.
London: Academic Press: 1980, pp. 215-252 - ↑
Los, S.A., & Schut, M.L. (2008).
The effective time course of preparation. Cognitive psychology, 57(1), 20-55. [PubMed:18255052] [WorldCat] [DOI] - ↑
BOTWINICK, J., & BRINLEY, J.F. (1962).
An analysis of set in relation to reaction time. Journal of experimental psychology, 63, 568-74. [PubMed:13871720] [WorldCat] [DOI] - ↑ 34.0 34.1 34.2
FOLEY, P.J. (1959).
The foreperiod and simple reaction time. Canadian journal of psychology, 13(1), 20-2. [PubMed:13629396] [WorldCat] - ↑
KARLIN, L. (1959).
Reaction time as a function of foreperiod duration and variability. Journal of experimental psychology, 58, 185-91. [PubMed:14404508] [WorldCat] [DOI] - ↑ FPがランダムに変化する場合には、この現象は現れにくい。 FPの長さに関係なく、もともとFPを正確に予測できないからである。
- ↑
DRAZIN, D.H. (1961).
Effects of foreperiod, foreperiod variability, and probability of stimulus occurrence on simple reaction time. Journal of experimental psychology, 62, 43-50. [PubMed:13724295] [WorldCat] [DOI] - ↑
Donchin, E., & Lindsley, D.B. (1966).
Average evoked potentials and reaction times to visual stimuli. Electroencephalography and clinical neurophysiology, 20(3), 217-23. [PubMed:4160389] [WorldCat] [DOI] - ↑
Menon, R.S., Luknowsky, D.C., & Gati, J.S. (1998).
Mental chronometry using latency-resolved functional MRI. Proceedings of the National Academy of Sciences of the United States of America, 95(18), 10902-7. [PubMed:9724802] [PMC] [WorldCat] [DOI] - ↑
Teichner, W.H., & Krebs, M.J. (1972).
Laws of the simple visual reaction time. Psychological review, 79(4), 344-58. [PubMed:5038152] [WorldCat] [DOI] - ↑
Ueno, T. (1977).
Reaction time as a measure of temporal summation at suprathreshold levels. Vision research, 17(2), 227-32. [PubMed:867843] [WorldCat] [DOI] - ↑
H G Murray
Stimulus intensity and reaction time: Evaluation of a decision-theory model.
J Exp Psychol: 1970, 84;383-391 - ↑
M J Nissen
Stimulus intensity and information processing.
Percept Pstchophys: 1977, 22;338-352 - ↑
Pins, D., & Bonnet, C. (1996).
On the relation between stimulus intensity and processing time: Piéron's law and choice reaction time. Perception & psychophysics, 58(3), 390-400. [PubMed:8935900] [WorldCat] [DOI] - ↑
J M T Brebner, A T Welford
Introduction: an historical sketch. In A T Welford (ed.) Reaction times.
London: Academic Press: 1980, pp. 1-23 - ↑ 46.0 46.1 46.2
大山 正
反応時間研究の歴史と現状
人間工学: 1985, 21;57-64 - ↑
Kohfeld, D.L. (1971).
Simple reaction time as a function of stimulus intensity in decibels of light and sound. Journal of experimental psychology, 88(2), 251-7. [PubMed:5577177] [WorldCat] [DOI] - ↑
Nickerson, R.S. (1973).
Intersensory facilitation of reaction time: energy summation or preparation enhancement? Psychological review, 80(6), 489-509. [PubMed:4757060] [WorldCat] [DOI] - ↑ 49.0 49.1 49.2 49.3
S H Seashore, R H Seashore
Individual differences in simple auditory reaction times of hands, feet and jaws.
J Exp Psychol: 1941, 29(4); 342-345 - ↑
田島 誠
反応時間
山﨑昌廣、坂本和義、関 邦博(編) 人間の許容限界事典
東京: 朝倉書店:2005, pp. 445-448. - ↑ 51.0 51.1 51.2
Simon, J.R. (1967).
Ear preference in a simple reaction-time task. Journal of experimental psychology, 75(1), 49-55. [PubMed:6065838] [WorldCat] [DOI] - ↑ 52.0 52.1
Rabbitt, P. (1978).
Hand dominance, attention, and the choice between responses. The Quarterly journal of experimental psychology, 30(3), 407-16. [PubMed:693786] [WorldCat] [DOI] - ↑
KERR, M., MINGAY, R., & ELITHORN, A. (1963).
CEREBRAL DOMINANCE IN REACTION TIME RESPONSES. British journal of psychology (London, England : 1953), 54, 325-36. [PubMed:14079023] [WorldCat] [DOI] - ↑ 54.0 54.1
D Elliott, E A Roy, D Goodman, R G Carson, R Chua, B K V Maraj
Asymmetries in the preparation and control of manual aiming movements.
Can J Exp Psychol: 1993, 47;570-589 - ↑
Carson, R.G., Chua, R., Elliott, D., & Goodman, D. (1990).
The contribution of vision to asymmetries in manual aiming. Neuropsychologia, 28(11), 1215-20. [PubMed:2290495] [WorldCat] [DOI] - ↑
Annett, M., & Annett, J. (1979).
Individual differences in right and left reaction time. British journal of psychology (London, England : 1953), 70(3), 393-404. [PubMed:486877] [WorldCat] [DOI] - ↑ 57.0 57.1
MINUCCI, P.K., & CONNORS, M.M. (1964).
REACTION TIME UNDER THREE VIEWING CONDITIONS: BINOCULAR, DOMINANT EYE, AND NONDOMINANT EYE. Journal of experimental psychology, 67, 268-75. [PubMed:14129728] [WorldCat] [DOI] - ↑ 58.0 58.1
FITTS, P.M., & SEEGER, C.M. (1953).
S-R compatibility: spatial characteristics of stimulus and response codes. Journal of experimental psychology, 46(3), 199-210. [PubMed:13084867] [WorldCat] [DOI] - ↑
R W Proctor, T G Reeve (eds.)
Stimulus-response compatibility: An integrated perspective.
Amsterdam: North-Holland: 1990 - ↑ 60.0 60.1
Wallace, R.J. (1971).
S-R compatibility and the idea of a response code. Journal of experimental psychology, 88(3), 354-60. [PubMed:5090926] [WorldCat] [DOI] - ↑
Simon, J.R., Hinrichs, J.V., & Craft, J.L. (1970).
Auditory S-R compatibility: reaction time as a function of ear-hand correspondence and ear-response-location correspondence. Journal of experimental psychology, 86(1), 97-102. [PubMed:5482039] [WorldCat] [DOI] - ↑
Peters, M. (1983).
RT to tactile stimuli presented ipsi- and contralaterally to the responding hand. The Quarterly journal of experimental psychology. A, Human experimental psychology, 35(Pt 2), 397-410. [PubMed:6571317] [WorldCat] - ↑
L Riggio, L de G Gawryszewski, C Umiltà
What is crossed in crossed-hand effects?
Acta Psychol (Amst): 1986, 62;89-100 - ↑
Buck, L. (1966).
Reaction time as a measure of perceptual vigilance. Psychological bulletin, 65(5), 291-304. [PubMed:5325893] [WorldCat] [DOI] - ↑
Langner, R., Willmes, K., Chatterjee, A., Eickhoff, S.B., & Sturm, W. (2010).
Energetic effects of stimulus intensity on prolonged simple reaction-time performance. Psychological research, 74(5), 499-512. [PubMed:20146071] [WorldCat] [DOI] - ↑ 66.0 66.1 66.2 66.3 66.4
A T Welford
Relationshipes between reaction time and fatigue, stress age and sex.
In A T Welford (ed.) Reaction times. London: Academic Press: 1980, pp. 321-354 - ↑
Steinbach, T., von Dreden, G., & Pöppel, E. (1991).
Long-term training in a choice reaction time task reveals different learning characteristics for the visual and auditory system. Die Naturwissenschaften, 78(4), 185-7. [PubMed:1852216] [WorldCat] [DOI] - ↑ 68.0 68.1 68.2
Williams, B.R., Hultsch, D.F., Strauss, E.H., Hunter, M.A., & Tannock, R. (2005).
Inconsistency in reaction time across the life span. Neuropsychology, 19(1), 88-96. [PubMed:15656766] [WorldCat] [DOI] - ↑
Cerella, J. (1985).
Information processing rates in the elderly. Psychological bulletin, 98(1), 67-83. [PubMed:4034819] [WorldCat] - ↑ 70.0 70.1 70.2
Fozard, J.L., Vercryssen, M., Reynolds, S.L., Hancock, P.A., & Quilter, R.E. (1994).
Age differences and changes in reaction time: the Baltimore Longitudinal Study of Aging. Journal of gerontology, 49(4), P179-89. [PubMed:8014399] [WorldCat] [DOI] - ↑ 71.0 71.1 71.2
Anstey, K.J., Dear, K., Christensen, H., & Jorm, A.F. (2005).
Biomarkers, health, lifestyle, and demographic variables as correlates of reaction time performance in early, middle, and late adulthood. The Quarterly journal of experimental psychology. A, Human experimental psychology, 58(1), 5-21. [PubMed:15881288] [WorldCat] [DOI] - ↑ 72.0 72.1
時任真一郎、西平賀昭、八田有洋、秋山幸代、和坂俊昭、金田健史、麓 正樹
前期高齢者の反応時間低下のメカニズムに関する研究 ―課題遂行による差異から―
体力科学: 2001, 50;303-312 - ↑ 73.0 73.1
Der, G., & Deary, I.J. (2006).
Age and sex differences in reaction time in adulthood: results from the United Kingdom Health and Lifestyle Survey. Psychology and aging, 21(1), 62-73. [PubMed:16594792] [WorldCat] [DOI] - ↑
飯田悠佳子、宮崎 真、関口浩文、上田有吾、鳥居 俊、内田 直
前思春期男女児童の日常身体活動の特性と視覚性Go/Nogo課題応答性
発育発達研究: 2010, 45;1-10 - ↑
Lieberman, H.R., Wurtman, R.J., Emde, G.G., Roberts, C., & Coviella, I.L. (1987).
The effects of low doses of caffeine on human performance and mood. Psychopharmacology, 92(3), 308-12. [PubMed:3114783] [WorldCat] [DOI] - ↑ 76.0 76.1
Kerr, J.S., Sherwood, N., & Hindmarch, I. (1991).
Separate and combined effects of the social drugs on psychomotor performance. Psychopharmacology, 104(1), 113-9. [PubMed:1881996] [WorldCat] [DOI] - ↑
Hindmarch, I., Kerr, J.S., & Sherwood, N. (1990).
Effects of nicotine gum on psychomotor performance in smokers and non-smokers. Psychopharmacology, 100(4), 535-41. [PubMed:2320715] [WorldCat] [DOI] - ↑
Maylor, E.A., & Rabbitt, P.M. (1993).
Alcohol, reaction time and memory: a meta-analysis. British journal of psychology (London, England : 1953), 84 ( Pt 3), 301-17. [PubMed:8401986] [WorldCat] [DOI] - ↑
倪 臻、笠井達哉、長谷川善輝、林 司佳子、矢作 晋
アルコール摂取がヒトの反応時間及び運動野の抑制回路に及ぼす影響
日本運動生理学雑誌: 2003, 10;55-63 - ↑
Dawson, J., Boyle, J., Stanley, N., Johnsen, S., Hindmarch, I., & Skene, D.J. (2008).
Benzodiazepine-induced reduction in activity mirrors decrements in cognitive and psychomotor performance. Human psychopharmacology, 23(7), 605-13. [PubMed:18570226] [WorldCat] [DOI] - ↑
Ulrich, R., Rinkenauer, G., & Miller, J. (1998).
Effects of stimulus duration and intensity on simple reaction time and response force. Journal of experimental psychology. Human perception and performance, 24(3), 915-28. [PubMed:9627425] [WorldCat] [DOI] - ↑
RAAB, D.H. (1962).
Effect of stimulus-duration on auditory reaction-time. The American journal of psychology, 75, 298-301. [PubMed:14489536] [WorldCat] - ↑
RAINS, J.D. (1963).
SIGNAL LUMINANCE AND POSITION EFFECTS IN HUMAN REACTION TIME. Vision research, 61, 239-51. [PubMed:14168292] [WorldCat] [DOI] - ↑ 84.0 84.1
Lupp, U., Hauske, G., & Wolf, W. (1976).
Perceptual latencies to sinusoidal gratings. Vision research, 16(9), 969-72. [PubMed:948887] [WorldCat] [DOI] - ↑
Lisper, H.O., & Kjellberg, A. (1972).
Effects of 24-hour sleep deprivation on rate of decrement in a 10-minute auditory reaction time task. Journal of experimental psychology, 96(2), 287-90. [PubMed:4645958] [WorldCat] [DOI] - ↑
Tomporowski, P.D. (2003).
Effects of acute bouts of exercise on cognition. Acta psychologica, 112(3), 297-324. [PubMed:12595152] [WorldCat] - ↑
Kida, N., Oda, S., & Matsumura, M. (2005).
Intensive baseball practice improves the Go/Nogo reaction time, but not the simple reaction time. Brain research. Cognitive brain research, 22(2), 257-64. [PubMed:15653298] [WorldCat] [DOI] - ↑ 例えば心的回転(mental rotation)で、図形の回転角度に比例した反応時間は、 心的イメージが刺激のアナログ的な表象である証拠と解釈された。 しかしこの解釈には反論が多く、心理学上の論争となった(イメージ論争)。 また視覚探索(visual search, 例えば画面上の10個の物体の中から目的の物体を探し出す課題)では、 反応時間が物体数に比例して長くなることがあるが、 これが逐次的情報処理(物体を1つずつ処理する)の反映なのか、 並列的情報処理(複数物体を同時に処理する)の速さが変化することの反映なのか、 しばしば議論となる。
- ↑
I W Silverman
Sex differences in simple visual reaction time: A historical meta-analysis.
Sex Roles: 2006, 54;57-68 - ↑
英:chronoscope 機械式の精密な計時装置。下記文献等を参照。
苧阪直行
実験心理学の誕生と展開 実験機器と史料からたどる日本心理学史
京都大学学術出版会: 2000 - ↑ 特に、視覚刺激を一般的なディスプレイ装置で提示する場合には、時間解像度があまり高くないことに留意する必要がある。 例えばリフレッシュレートが60Hzならば、視覚刺激は16.7 msの単位でしか操作できない。 精密な実験では、フォトダイオードなどを用いて実際に画面が刺激光を発する時間を確かめるべきである。
- ↑
Wolfe, J.M., Horowitz, T.S., & Kenner, N.M. (2005).
Cognitive psychology: rare items often missed in visual searches. Nature, 435(7041), 439-40. [PubMed:15917795] [PMC] [WorldCat] [DOI]
(執筆者:新美亮輔・横澤一彦、担当編集委員:)












