「機能的結合」の版間の差分
細編集の要約なし |
細編集の要約なし |
||
| (同じ利用者による、間の1版が非表示) | |||
| 2行目: | 2行目: | ||
<font size="+1">[https://researchmap.jp/mfukushima 福嶋 誠]</font><br> | <font size="+1">[https://researchmap.jp/mfukushima 福嶋 誠]</font><br> | ||
''奈良先端科学技術大学院大学 先端科学技術研究科 情報科学領域''<br> | ''奈良先端科学技術大学院大学 先端科学技術研究科 情報科学領域''<br> | ||
DOI:<selfdoi /> | DOI:<selfdoi /> 原稿受付日:2021年7月19日 原稿完成日:2021年10月XX日<br> | ||
担当編集委員:[https://researchmap.jp/kkitajo 北城 圭一](生理学研究所)<br> | 担当編集委員:[https://researchmap.jp/kkitajo 北城 圭一](生理学研究所)<br> | ||
</div> | </div> | ||
| 24行目: | 24行目: | ||
上に挙げた指標は、すべて因果性を仮定しない向きなしの統計的依存性の定量化に用いられる指標であるが、向きありの統計的依存性を定量化する際に用いられる代表的な因果性の定義としては[[グレンジャー因果性]]<ref name=Granger1969>'''Granger, C.W. (1969).'''<br>Investigating causal relations by econometric models and cross-spectral methods. Econometrica: journal of the Econometric Society, 37(3), 424-38. [https://doi.org/10.2307/1912791 PDF]</ref>が挙げられる。グレンジャー因果性の定義では、「AとBの過去の値を用いた場合のBの値の予測精度が、Bのみの過去の値を用いた場合のBの値の予測精度よりも高いとき、AはBの原因である(A causes B)」とされる。グレンジャー因果性を計算する際には、[[ベクトル自己回帰モデル]]によって[[多変量時系列]]がモデル化され、本モデルに基づいた統計量からグレンジャー因果性の評価に用いられるさまざまな定量化指標<ref name=Geweke1984>'''Geweke, J.F. (1984).'''<br>Measures of conditional linear dependence and feedback between time series. Journal of the American Statistical Association, 79(388), 907-15.</ref> <ref name=Baccala2001><pubmed>11417058</pubmed></ref>が計算される。 | 上に挙げた指標は、すべて因果性を仮定しない向きなしの統計的依存性の定量化に用いられる指標であるが、向きありの統計的依存性を定量化する際に用いられる代表的な因果性の定義としては[[グレンジャー因果性]]<ref name=Granger1969>'''Granger, C.W. (1969).'''<br>Investigating causal relations by econometric models and cross-spectral methods. Econometrica: journal of the Econometric Society, 37(3), 424-38. [https://doi.org/10.2307/1912791 PDF]</ref>が挙げられる。グレンジャー因果性の定義では、「AとBの過去の値を用いた場合のBの値の予測精度が、Bのみの過去の値を用いた場合のBの値の予測精度よりも高いとき、AはBの原因である(A causes B)」とされる。グレンジャー因果性を計算する際には、[[ベクトル自己回帰モデル]]によって[[多変量時系列]]がモデル化され、本モデルに基づいた統計量からグレンジャー因果性の評価に用いられるさまざまな定量化指標<ref name=Geweke1984>'''Geweke, J.F. (1984).'''<br>Measures of conditional linear dependence and feedback between time series. Journal of the American Statistical Association, 79(388), 907-15.</ref> <ref name=Baccala2001><pubmed>11417058</pubmed></ref>が計算される。 | ||
グレンジャー因果性とは異なり[[ベクトル自己回帰モデル]]を仮定せずに、[[情報量]]ベースで向きありの統計的依存性を定量化する指標には[[移動エントロピー]]<ref name=Vicente2011><pubmed>20706781</pubmed></ref>がある。なお、因果性を仮定した向きありの統計的依存性を定量化するこれらの指標は、後述する有効結合の推定値としてみなされる場合がある<ref name=Vicente2011 /><ref name=Friston2011><pubmed>22432952</pubmed></ref>。 | グレンジャー因果性とは異なり[[ベクトル自己回帰モデル]]を仮定せずに、[[情報量]]ベースで向きありの統計的依存性を定量化する指標には[[移動エントロピー]]<ref name=Vicente2011><pubmed>20706781</pubmed></ref>[12]がある。なお、因果性を仮定した向きありの統計的依存性を定量化するこれらの指標は、後述する有効結合の推定値としてみなされる場合がある<ref name=Vicente2011 /><ref name=Friston2011><pubmed>22432952</pubmed></ref>。 | ||
その他、神経細胞の離散的な[[スパイク]]活動時系列に対しては、二時系列間の相互相関関数を用いて統計的依存性を定量化する方法が用いられている<ref name=Perkel1967><pubmed>4292792</pubmed></ref>。また、統計的依存性を直接定量化せずに、全活動時系列行列に対し独立成分分析を適用することによって同期的に活動が生じている脳領野を同定する方法も、特に安静時に取得された[[機能的磁気共鳴画像]]([[functional magnetic resonance imaging]]; [[fMRI]])データに対してよく用いられる<ref name=Damoiseaux2006><pubmed>16945915</pubmed></ref>。 | その他、神経細胞の離散的な[[スパイク]]活動時系列に対しては、二時系列間の相互相関関数を用いて統計的依存性を定量化する方法が用いられている<ref name=Perkel1967><pubmed>4292792</pubmed></ref>。また、統計的依存性を直接定量化せずに、全活動時系列行列に対し独立成分分析を適用することによって同期的に活動が生じている脳領野を同定する方法も、特に安静時に取得された[[機能的磁気共鳴画像]]([[functional magnetic resonance imaging]]; [[fMRI]])データに対してよく用いられる<ref name=Damoiseaux2006><pubmed>16945915</pubmed></ref>。 | ||
| 31行目: | 31行目: | ||
機能的結合と対となる用語としては[[構造的結合]](structural connectivity)がある。構造的結合は、巨視的スケールにおいては脳領野間の[[白質]]を介した解剖学的な接続性のことを指し<ref name=Hagmann2008><pubmed>18597554</pubmed></ref>、安静時における機能的結合と関連があることが知られている。 | 機能的結合と対となる用語としては[[構造的結合]](structural connectivity)がある。構造的結合は、巨視的スケールにおいては脳領野間の[[白質]]を介した解剖学的な接続性のことを指し<ref name=Hagmann2008><pubmed>18597554</pubmed></ref>、安静時における機能的結合と関連があることが知られている。 | ||
例えば、安静時fMRIデータから求められた機能的結合の強度と[[拡散磁気共鳴画像]]([[diffusion MRI]])データから求められた構造的結合の強度が正に相関すること<ref name=Honey2009><pubmed>19188601</pubmed></ref>、構造的結合に沿って神経細胞集団の活動ダイナミクスモデルを結合させた系から安静時機能的結合をシミュレートできること<ref name=Honey2009 />、構造的結合から求められるネットワーク上のコミュニケーション指標が安静時機能的結合をよく再現できること<ref name=Goni2014><pubmed>24379387</pubmed></ref>、などがこれまでに示されている。 | 例えば、安静時fMRIデータから求められた機能的結合の強度と[[拡散磁気共鳴画像]]([[diffusion MRI]])データから求められた構造的結合の強度が正に相関すること<ref name=Honey2009><pubmed>19188601</pubmed></ref>、構造的結合に沿って神経細胞集団の活動ダイナミクスモデルを結合させた系から安静時機能的結合をシミュレートできること<ref name=Honey2009 /> [17]、構造的結合から求められるネットワーク上のコミュニケーション指標が安静時機能的結合をよく再現できること<ref name=Goni2014><pubmed>24379387</pubmed></ref>、などがこれまでに示されている。 | ||
== 有効(または実効的)結合との関係 == | == 有効(または実効的)結合との関係 == | ||
2021年10月29日 (金) 16:12時点における版
福嶋 誠
奈良先端科学技術大学院大学 先端科学技術研究科 情報科学領域
DOI:10.14931/bsd.9954 原稿受付日:2021年7月19日 原稿完成日:2021年10月XX日
担当編集委員:北城 圭一(生理学研究所)
英:functional connectivity 独:funktionelle Konnektivität 仏:connectivité fonctionnelle
同義語:脳機能結合
脳神経科学分野における機能的結合とは、単一神経細胞レベルから脳領野レベルに至るまでのさまざまな空間スケールにおいて定量化された脳活動時系列間の統計的依存性のことを指す。統計的依存性を定量化する機能的結合の代表的な指標としては相関係数が挙げられ、異なる二つの神経細胞や脳領野などの活動時系列同士が互いに強く同期している場合、これらの間の機能的結合が強いと解釈される。機能的結合は、白質の解剖学的な接続性のことを指す構造的結合とも密接に関連しており、構造的結合の場合と同様に、個々の結合の性質のみならず、多数の結合から構成されたネットワークの性質を明らかにしようとする研究も進められている。また、機能的結合がどのように時間変化しているのかを明らかにしようとする研究や、機能的結合を個人の特定などのさまざまな用途に応用しようとする研究なども広く実施されるようになっている。
統計的依存性を定量化する機能的結合の指標
脳神経科学分野における機能的結合とは、定量化された脳活動時系列間の統計的依存性のことを指す。単一神経細胞レベルから脳領野レベルに至るまでのさまざまな空間スケールが対象となる。
統計的依存性を定量化する機能的結合の指標にはさまざまなものがある。最も単純な指標としては二時系列間の相関係数[1](図1)が挙げられる。相関係数は、活動時系列そのものに対して以外にも、活動時系列の特定の周波数成分に対して[2]や、活動時系列の特定の周波数成分の包絡線に対して[3]計算されることがある。
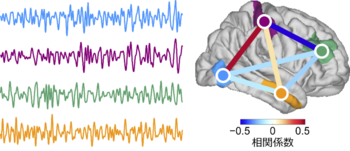
領野内で平均化されたヒト安静時機能的磁気共鳴画像(functional magnetic resonance imaging; fMRI)データ時系列と、これらの時系列間の相関係数の値を図示している。
相関係数には着目する二時系列以外からの間接的な影響が含まれるが、この影響を取り除くことを目的として計算される指標には偏相関係数[4]や正則化逆共分散(regularized inverse covariance)[5]がある。
また、より高次の統計量(相関係数は二次統計量)や非線形の統計的依存性までを反映する指標には相互情報量[6]が、周波数空間における統計的依存性を定量化する指標にはコヒーレンス[7]、位相ロック値(phase locking value)[8]などがある。
上に挙げた指標は、すべて因果性を仮定しない向きなしの統計的依存性の定量化に用いられる指標であるが、向きありの統計的依存性を定量化する際に用いられる代表的な因果性の定義としてはグレンジャー因果性[9]が挙げられる。グレンジャー因果性の定義では、「AとBの過去の値を用いた場合のBの値の予測精度が、Bのみの過去の値を用いた場合のBの値の予測精度よりも高いとき、AはBの原因である(A causes B)」とされる。グレンジャー因果性を計算する際には、ベクトル自己回帰モデルによって多変量時系列がモデル化され、本モデルに基づいた統計量からグレンジャー因果性の評価に用いられるさまざまな定量化指標[10] [11]が計算される。
グレンジャー因果性とは異なりベクトル自己回帰モデルを仮定せずに、情報量ベースで向きありの統計的依存性を定量化する指標には移動エントロピー[12][12]がある。なお、因果性を仮定した向きありの統計的依存性を定量化するこれらの指標は、後述する有効結合の推定値としてみなされる場合がある[12][13]。
その他、神経細胞の離散的なスパイク活動時系列に対しては、二時系列間の相互相関関数を用いて統計的依存性を定量化する方法が用いられている[14]。また、統計的依存性を直接定量化せずに、全活動時系列行列に対し独立成分分析を適用することによって同期的に活動が生じている脳領野を同定する方法も、特に安静時に取得された機能的磁気共鳴画像(functional magnetic resonance imaging; fMRI)データに対してよく用いられる[15]。
構造的結合との関係
機能的結合と対となる用語としては構造的結合(structural connectivity)がある。構造的結合は、巨視的スケールにおいては脳領野間の白質を介した解剖学的な接続性のことを指し[16]、安静時における機能的結合と関連があることが知られている。
例えば、安静時fMRIデータから求められた機能的結合の強度と拡散磁気共鳴画像(diffusion MRI)データから求められた構造的結合の強度が正に相関すること[17]、構造的結合に沿って神経細胞集団の活動ダイナミクスモデルを結合させた系から安静時機能的結合をシミュレートできること[17] [17]、構造的結合から求められるネットワーク上のコミュニケーション指標が安静時機能的結合をよく再現できること[18]、などがこれまでに示されている。
有効(または実効的)結合との関係
機能的結合と似た概念に有効結合(effective connectivity)がある。有効結合は、ある機能単位の神経細胞または神経細胞集団が他の機能単位に及ぼす影響として定義される[1]。機能的結合は、活動時系列間の統計的依存性として観測される現象に対応するのに対し、有効結合は、この現象を説明するためのモデルに含まれたパラメータに対応する[13]。
以上の定義のほかに、機能的結合の意味する範囲を「因果性を仮定しない向きなしの統計的依存性」に限局した上で、(前述したように)有効結合を「因果性を仮定する向きありの統計的依存性」と定義する場合もある。
有効結合の推定に用いられるモデルとしては、動的因果モデリング(dynamic causal modeling)[19]や構造方程式モデリング(structural equation modeling)[20]などがある。これらのモデルは当初計算量の問題から少数(数個)の機能単位間の有効結合の推定にしか適用できなかったが、多数(数十個)の機能単位間の有効結合を推定できるように動的因果モデリングを拡張する研究も進められている[21]。
機能的結合の解析
機能的結合に対しては、活動に対してと同様に、グループ間の違いや実験条件による違いを統計的検定によって明らかしようとする研究が数多くある[22]。機能的結合の次元は対象とする活動時系列の次元の二乗のオーダーであるため、多重比較補正を実施すると検出力が低くなりやすいが、これを改善するための方法としては、グラフ版のクラスタベースの統計量であるネットワークベース統計量(network-based statistic)[23]を用いた統計的検定手法が考案されている。
多数の機能単位間の機能的結合から構成されるネットワークは、機能的脳ネットワーク、または脳機能ネットワークと呼ばれる。ネットワーク科学分野で用いられてきたグラフ理論的解析手法の適用[24]を通して、機能的結合のネットワークとしてのさまざまな性質(例えば、ネットワーク内のモジュール構造[25]など)がこれまでに明らかにされてきた。
また機能的結合を全時間区間の活動時系列から求めるのではなく、短時間区間の時系列から機能的結合を求め,その時間変化(動的機能的結合,dynamic functional connectivity)に着目する研究も展開されている[26]。短時間の機能的結合を求める方法の例としては、移動時間窓を用いて短時間の統計的依存性を定量化する方法[27]、瞬時位相の類似度を計算する方法[28]、標準化後の二活動時系列ベクトル間の要素積を計算する方法[29]などがある。これらの方法を用いることによって、動的機能的結合のさまざまな性質(例えば、安静時fMRIデータから求められた動的機能的結合のネットワーク状態は、ネットワークのモジュール化度合いが強まった分離状態と弱まった統合状態の間で、常に時間的に変動していること[30][31]など)が明らかにされている。
応用
(主にヒトの)機能的結合をさまざまな用途に応用することを目指した研究も進められている。例としては、機能的都合およびその特徴量を用いて、個人の特定[32]、加齢の特徴づけ[33]、精神疾患バイオマーカーの開発[34]を試みた研究などが挙げられる。
関連項目
参考文献
- ↑ 1.0 1.1 Friston, K.R. (1994).
Functional and effective connectivity in neuroimaging: a synthesis. Human brain mapping, 2(1-2), 56-78. PDF - ↑
Fox, M.D., Snyder, A.Z., Vincent, J.L., Corbetta, M., Van Essen, D.C., & Raichle, M.E. (2005).
The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proceedings of the National Academy of Sciences of the United States of America, 102(27), 9673-8. [PubMed:15976020] [PMC] [WorldCat] [DOI] - ↑
Hipp, J.F., Hawellek, D.J., Corbetta, M., Siegel, M., & Engel, A.K. (2012).
Large-scale cortical correlation structure of spontaneous oscillatory activity. Nature neuroscience, 15(6), 884-90. [PubMed:22561454] [PMC] [WorldCat] [DOI] - ↑
Marrelec, G., Krainik, A., Duffau, H., Pélégrini-Issac, M., Lehéricy, S., Doyon, J., & Benali, H. (2006).
Partial correlation for functional brain interactivity investigation in functional MRI. NeuroImage, 32(1), 228-37. [PubMed:16777436] [WorldCat] [DOI] - ↑
Friedman, J., Hastie, T., & Tibshirani, R. (2008).
Sparse inverse covariance estimation with the graphical lasso. Biostatistics (Oxford, England), 9(3), 432-41. [PubMed:18079126] [PMC] [WorldCat] [DOI] - ↑ Shannon, C.E. (1948).
A mathematical theory of communication. The Bell system technical journal, 27(3), 379-423. PDF - ↑
Walter, D.O. (1963).
Spectral analysis for electroencephalograms: mathematical determination of neurophysiological relationships from records of limited duration. Experimental neurology, 8, 155-81. [PubMed:20191690] [WorldCat] [DOI] - ↑
Lachaux, J.P., Rodriguez, E., Martinerie, J., & Varela, F.J. (1999).
Measuring phase synchrony in brain signals. Human brain mapping, 8(4), 194-208. [PubMed:10619414] [PMC] [WorldCat] [DOI] - ↑ Granger, C.W. (1969).
Investigating causal relations by econometric models and cross-spectral methods. Econometrica: journal of the Econometric Society, 37(3), 424-38. PDF - ↑ Geweke, J.F. (1984).
Measures of conditional linear dependence and feedback between time series. Journal of the American Statistical Association, 79(388), 907-15. - ↑
Baccalá, L.A., & Sameshima, K. (2001).
Partial directed coherence: a new concept in neural structure determination. Biological cybernetics, 84(6), 463-74. [PubMed:11417058] [WorldCat] [DOI] - ↑ 12.0 12.1
Vicente, R., Wibral, M., Lindner, M., & Pipa, G. (2011).
Transfer entropy--a model-free measure of effective connectivity for the neurosciences. Journal of computational neuroscience, 30(1), 45-67. [PubMed:20706781] [PMC] [WorldCat] [DOI] - ↑ 13.0 13.1
Friston, K.J. (2011).
Functional and effective connectivity: a review. Brain connectivity, 1(1), 13-36. [PubMed:22432952] [WorldCat] [DOI] - ↑
Perkel, D.H., Gerstein, G.L., & Moore, G.P. (1967).
Neuronal spike trains and stochastic point processes. II. Simultaneous spike trains. Biophysical journal, 7(4), 419-40. [PubMed:4292792] [PMC] [WorldCat] [DOI] - ↑
Damoiseaux, J.S., Rombouts, S.A., Barkhof, F., Scheltens, P., Stam, C.J., Smith, S.M., & Beckmann, C.F. (2006).
Consistent resting-state networks across healthy subjects. Proceedings of the National Academy of Sciences of the United States of America, 103(37), 13848-53. [PubMed:16945915] [PMC] [WorldCat] [DOI] - ↑
Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C.J., Wedeen, V.J., & Sporns, O. (2008).
Mapping the structural core of human cerebral cortex. PLoS biology, 6(7), e159. [PubMed:18597554] [PMC] [WorldCat] [DOI] - ↑ 17.0 17.1
Honey, C.J., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J.P., Meuli, R., & Hagmann, P. (2009).
Predicting human resting-state functional connectivity from structural connectivity. Proceedings of the National Academy of Sciences of the United States of America, 106(6), 2035-40. [PubMed:19188601] [PMC] [WorldCat] [DOI] - ↑
Goñi, J., van den Heuvel, M.P., Avena-Koenigsberger, A., Velez de Mendizabal, N., Betzel, R.F., Griffa, A., ..., & Sporns, O. (2014).
Resting-brain functional connectivity predicted by analytic measures of network communication. Proceedings of the National Academy of Sciences of the United States of America, 111(2), 833-8. [PubMed:24379387] [PMC] [WorldCat] [DOI] - ↑
Friston, K.J., Harrison, L., & Penny, W. (2003).
Dynamic causal modelling. NeuroImage, 19(4), 1273-302. [PubMed:12948688] [WorldCat] [DOI] - ↑ Mclntosh, A.R., & Gonzalez-Lima, F. (1994).
Structural equation modeling and its application to network analysis in functional brain imaging. Human brain mapping, 2(1-2), 2-22 PDF - ↑
Razi, A., Seghier, M.L., Zhou, Y., McColgan, P., Zeidman, P., Park, H.J., ..., & Friston, K.J. (2017).
Large-scale DCMs for resting-state fMRI. Network neuroscience (Cambridge, Mass.), 1(3), 222-241. [PubMed:29400357] [PMC] [WorldCat] [DOI] - ↑
Rogers, B.P., Morgan, V.L., Newton, A.T., & Gore, J.C. (2007).
Assessing functional connectivity in the human brain by fMRI. Magnetic resonance imaging, 25(10), 1347-57. [PubMed:17499467] [PMC] [WorldCat] [DOI] - ↑
Zalesky, A., Fornito, A., & Bullmore, E.T. (2010).
Network-based statistic: identifying differences in brain networks. NeuroImage, 53(4), 1197-207. [PubMed:20600983] [WorldCat] [DOI] - ↑
Rubinov, M., & Sporns, O. (2010).
Complex network measures of brain connectivity: uses and interpretations. NeuroImage, 52(3), 1059-69. [PubMed:19819337] [WorldCat] [DOI] - ↑
Sporns, O., & Betzel, R.F. (2016).
Modular Brain Networks. Annual review of psychology, 67, 613-40. [PubMed:26393868] [PMC] [WorldCat] [DOI] - ↑
Hutchison, R.M., Womelsdorf, T., Allen, E.A., Bandettini, P.A., Calhoun, V.D., Corbetta, M., ..., & Chang, C. (2013).
Dynamic functional connectivity: promise, issues, and interpretations. NeuroImage, 80, 360-78. [PubMed:23707587] [PMC] [WorldCat] [DOI] - ↑
Allen, E.A., Damaraju, E., Plis, S.M., Erhardt, E.B., Eichele, T., & Calhoun, V.D. (2014).
Tracking whole-brain connectivity dynamics in the resting state. Cerebral cortex (New York, N.Y. : 1991), 24(3), 663-76. [PubMed:23146964] [PMC] [WorldCat] [DOI] - ↑
Glerean, E., Salmi, J., Lahnakoski, J.M., Jääskeläinen, I.P., & Sams, M. (2012).
Functional magnetic resonance imaging phase synchronization as a measure of dynamic functional connectivity. Brain connectivity, 2(2), 91-101. [PubMed:22559794] [PMC] [WorldCat] [DOI] - ↑
Faskowitz, J., Esfahlani, F.Z., Jo, Y., Sporns, O., & Betzel, R.F. (2020).
Edge-centric functional network representations of human cerebral cortex reveal overlapping system-level architecture. Nature neuroscience, 23(12), 1644-1654. [PubMed:33077948] [WorldCat] [DOI] - ↑
Betzel, R.F., Fukushima, M., He, Y., Zuo, X.N., & Sporns, O. (2016).
Dynamic fluctuations coincide with periods of high and low modularity in resting-state functional brain networks. NeuroImage, 127, 287-297. [PubMed:26687667] [PMC] [WorldCat] [DOI] - ↑
Shine, J.M., Bissett, P.G., Bell, P.T., Koyejo, O., Balsters, J.H., Gorgolewski, K.J., ..., & Poldrack, R.A. (2016).
The Dynamics of Functional Brain Networks: Integrated Network States during Cognitive Task Performance. Neuron, 92(2), 544-554. [PubMed:27693256] [PMC] [WorldCat] [DOI] - ↑
Finn, E.S., Shen, X., Scheinost, D., Rosenberg, M.D., Huang, J., Chun, M.M., ..., & Constable, R.T. (2015).
Functional connectome fingerprinting: identifying individuals using patterns of brain connectivity. Nature neuroscience, 18(11), 1664-71. [PubMed:26457551] [PMC] [WorldCat] [DOI] - ↑
Chan, M.Y., Park, D.C., Savalia, N.K., Petersen, S.E., & Wig, G.S. (2014).
Decreased segregation of brain systems across the healthy adult lifespan. Proceedings of the National Academy of Sciences of the United States of America, 111(46), E4997-5006. [PubMed:25368199] [PMC] [WorldCat] [DOI] - ↑
Yahata, N., Morimoto, J., Hashimoto, R., Lisi, G., Shibata, K., Kawakubo, Y., ..., & Kawato, M. (2016).
A small number of abnormal brain connections predicts adult autism spectrum disorder. Nature communications, 7, 11254. [PubMed:27075704] [PMC] [WorldCat] [DOI]