「眼球運動」の版間の差分
細 →角膜反射法 |
細 →特徴 |
||
| (同じ利用者による、間の14版が非表示) | |||
| 1行目: | 1行目: | ||
{{box|text= 眼球運動は、ほぼ球体の眼球が眼窩内で回転軸を中心に回転する運動である。その運動は、眼球に付着し、互いに拮抗する3対(上直筋-下直筋、外直筋-内直筋、上斜筋―下斜筋、計6本、左右の眼で12本)の外眼筋を収縮、弛緩させることにより遂行される。眼球運動によって視覚対象へ視線を向けるまたは保持することが可能となり、視覚を適切に働かせることができる。眼球運動には、前庭動眼反射、視運動正反応、衝動性眼球運動(サッケード)、追跡眼球運動、輻輳・開散運動、固視微動など様式や機能の異なるものがある。}} | {{box|text= 眼球運動は、ほぼ球体の眼球が眼窩内で回転軸を中心に回転する運動である。その運動は、眼球に付着し、互いに拮抗する3対(上直筋-下直筋、外直筋-内直筋、上斜筋―下斜筋、計6本、左右の眼で12本)の外眼筋を収縮、弛緩させることにより遂行される。眼球運動によって視覚対象へ視線を向けるまたは保持することが可能となり、視覚を適切に働かせることができる。眼球運動には、前庭動眼反射、視運動正反応、衝動性眼球運動(サッケード)、追跡眼球運動、輻輳・開散運動、固視微動など様式や機能の異なるものがある。}} | ||
== 特徴 == | == 特徴 == | ||
[[ファイル:Saito eye movement Fig1.png|サムネイル|'''図1. 眼球をそれぞれの回転軸を中心に回転させたときの回旋眼位'''<br>文献<ref name=鈴木康夫1997 /><ref name=鈴木康夫2017 />を参考に作成。]] | [[ファイル:Saito eye movement Fig1.png|サムネイル|'''図1. 眼球をそれぞれの回転軸を中心に回転させたときの回旋眼位'''<br>文献<ref name=鈴木康夫1997 /><ref name=鈴木康夫2017 />を参考に作成。]] | ||
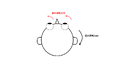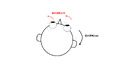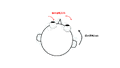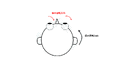
眼球の位置(眼位)は慣例的に、正面を向いて視覚対象が中心窩に投影される位置に眼を向けているときを第一眼位(primary position)、視線が第一眼位から水平または垂直のみに向けられるときを第二眼位(secondary position)、それ以外の方向へ向けられたときを第三眼位(tertiary position)と定義される<ref name=Carpenter1988>'''Carpenter R.H.S. (1988).'''<br>Movements of eyes (2nd edn): Pion Press, London.</ref>。眼球運動は、互いに直交する3つの回転軸(水平、垂直、回旋)を中心に生じる回転運動であるため、第三眼位(つまり、斜め方向へ)へ眼を向ける際に、回転する順序によって視線移動後の回旋眼位は異なると考えられる。つまり、第三眼位への視線移動の際、例えば、水平軸を中心に回転した後、垂直軸を中心に回転する場合(Helmholtzの座標系と呼ばれる)と垂直軸を中心に回転した後、水平軸を中心に回転した場合(Fickの座標系と呼ばれる)では回旋眼位が異なる('''図1''')。しかし、実際には、第三眼位への視線移動はどの順序で行われたかに関係なく眼球は眼窩内で一定の位置を向いているため、第三眼位は第一眼位から1回の回転で到達する眼位とみなすことができる。 | |||
これはオランダの眼科医であるDondersが提唱し(Dondersの法則)、ドイツの数学者であるListingが数学的に定義した<ref name=鈴木康夫1997>'''鈴木康夫 (1997).'''<br>なぜ今 Listingの法則なのか?. Equilibrium Research. 56(5):401-12.</ref><ref name=鈴木康夫2017>'''鈴木康夫 (2017).'''<br>回転として眼球運動を考えよう! Listingの法則とは?. 神経眼科. 34(2):139-47.</ref>。特に、Listingが述べた内容は「Listingの法則」と呼ばれ、視線移動は第一眼位の方向に直交する平面(Listingの平面)内にある軸を中心に1回転することで全ての眼位に到達すると考えられている('''図1''')。そのため、三次元の眼球運動は水平成分と垂直成分のみで表現できる(別の言い方をすれば、「振幅」と「方向」で表すことができる)<ref name=フィンドレイ2006>'''フィンドレイ JM, ギルクリスト, I.D., 本田仁視(監訳)(2006).'''<br>アクティブ・ビジョン 眼球運動の心理・神経科学: 北大路書房.</ref>。 | |||
== 役割 == | == 役割 == | ||
眼球運動の目的は視覚を適切に機能させることであり、その目的から眼球運動は2つの役割に大別される。一つは体(特に頭部)が動いている最中または周りがゆっくり動いている最中に視線の方向を視覚対象へ安定に保つこと(視線保持、gaze holding)であり、もう一つは視覚対象に中心窩を向けること(中心窩視、foveation)である(<ref name=Carpenter1988> </ref><ref name=Leigh2015> </ref> )。運動時に眼を固定した状態では体(頭部)の動きに合わせて視線も動いてしまうため、視覚像がブレてしまいはっきりと見ることができない。しかし、我々は周りの風景を楽しみながら散歩したり、飛んでくるボールを見ながら落下地点まで走ったりすることができる。これは頭部の動きに合わせて眼が動くため、それにより運動時でも視線を保つことができる。また、光を受容する視細胞は網膜に均等には分布しておらず、特に視覚対象の認識に関与する錐体は中心窩に密集している。従って、中心窩から外れたところにある視覚対象を認識するためには、眼を動かせて中心窩をその対象に向ける必要がある。視線保持に関与する眼球運動は反射であり、中心窩視に関与する眼球運動は随意運動(無意識でも生じる場合がある)である。 | |||
== 機能に基づく分類 == | == 機能に基づく分類 == | ||
眼球運動は両眼が同じ方向へ動く共同性眼球運動と反対方向へ動く非共同性眼球運動に分かれる。下記の眼球運動のうち、1-4は共同性眼球運動、5は非共同性眼球運動である。また、前述の眼球運動の役割のうち、1-2は視線保持に関与し3-5は中心窩視に関与する。 | |||
#''' | #'''前庭動眼反射(前庭眼反射)vestibulo-ocular reflex (VOR)(図2-1)'''<br>頭部が動いたときにこの動きと反対方向に眼球を動かすことで網膜に映る外界の像のブレを防ぐ反射(詳細は脳科学辞典「前庭動眼反射」の項を参照)。 | ||
#''' | #'''視運動性反応(視機性眼球反応)optokinetic response (OKR)(図2-2)'''<br>まわりの視野がゆっくり動く時に、網膜に映る外界の像がブレないように周りと同じ方向に眼が動く反射(詳細は脳科学辞典「視運動性眼振」の項を参照)。 | ||
#''' | #'''衝動性眼球運動(サッケード)saccade(図2-3)''' <br>中心窩視を得るために生じるすばやい眼球運動で、眼球速度は最大1000°/s-1 にまで達する。VORやOKRによる目の動きをリセットするすばやい目の動き(急速相)から生じたとされている(<ref name=Carpenter1988> </ref><ref name=Leigh2015>'''Leigh RJ, Zee, D.S. (2015).'''<br>The Neurology of Eye Movements (5th ed): Oxford University Press.</ref> )。 | ||
#''' | #'''追跡眼球運動(滑動性追跡眼球運動) pursuit eye movement (smooth pursuit)(図2-4)''' <br>ゆっくり動く視覚対象物の網膜像を網膜中心窩付近に維持し、その動きに合わせて視線を滑らかに動かす眼球運動(詳細は脳科学辞典「追跡眼球運動」の項を参照)。 | ||
#''' | #'''輻輳・開散運動 vergence (convergence・divergence)(図2-5)'''<br>観察者から異なる距離(奥行き)にある対象物に視線を移動させた時に起こる両眼が違う方向に動く眼球運動。輻輳は視覚対象が遠位から近づくとき、開散は近位から遠ざかるときの眼球運動をいう。(詳細は脳科学辞典「輻輳開散運動」の項を参照)。 | ||
<gallery> | <gallery> | ||
ファイル:Saito eye movement Fig2-1.gif|'''図2-1. 前庭動眼反射の時の眼の動き'''<br>頭部の動きと逆向きに眼が動く。 | ファイル:Saito eye movement Fig2-1.gif|'''図2-1. 前庭動眼反射の時の眼の動き'''<br>頭部の動きと逆向きに眼が動く。 | ||
| 33行目: | 24行目: | ||
ファイル:Saito eye movement Fig2-5.gif|'''図2-5. 輻輳・開散時の眼の動き'''<br>左右の眼がそれぞれ異なる方向へ動く。 | ファイル:Saito eye movement Fig2-5.gif|'''図2-5. 輻輳・開散時の眼の動き'''<br>左右の眼がそれぞれ異なる方向へ動く。 | ||
</gallery> | </gallery> | ||
上記の5つの眼球運動に加えて、固視微動 fixation nystagmus, fixation eye movementという眼球運動もみられる(<ref name=Martinez-Conde2007><pubmed>17894173</pubmed></ref> )。前述の通り、視覚対象に視線を一定に保つことで視覚認識が行われるが、視線が全く動かないと、時間と共に視覚刺激に対し反応しにくくなる(<ref name=Pritchard1961><pubmed>13738093</pubmed></ref> )。固視微動は不随意的な眼球運動で、網膜像を絶えず変化させることによって視覚入力を絶えず生成する役割がある。固視微動は眼球速度によってトレモア(tremor)、ドリフト(drift)、マイクロサッケード(microsaccade)の3種類ある(詳細は脳科学辞典「マイクロサッケード」の項を参照)。 | |||
== 神経経路 == | == 神経経路 == | ||
[[ファイル:Saito eye movement Fig3.png|サムネイル|'''図3. 眼球の動きに関与する外眼筋'''<br> | [[ファイル:Saito eye movement Fig3.png|サムネイル|'''図3. 眼球の動きに関与する外眼筋'''<br>カンデル神経科学第2版 図35-1((株)メディカル・サイエンス・インターナショナルからの転載許可を得て掲載)。]] | ||
[[ファイル:Saito eye movement Fig4.png|サムネイル|''' | [[ファイル:Saito eye movement Fig4.png|サムネイル|'''図3. 眼球の動きに関与する脳幹の神経核'''<br>カンデル神経科学第2版 図35-3((株)メディカル・サイエンス・インターナショナルからの転載許可を得て掲載)。]] | ||
眼球に付着する6本の外眼筋('''図3''')(<ref name=Kandel2022>'''Kandel E.R., Koester J., Mack S., Siegelbaum S., 宮下 保, 岡野 栄, et al. (2022).'''<br>カンデル神経科学. 第2版 ed: メディカル・サイエンス・インターナショナル xlviii, 1653p p.</ref> )は脳幹の動眼神経核、滑車神経核、外転神経核を起始核とする第Ⅲ脳神経(動眼神経)、第Ⅳ脳神経(滑車神経)、第Ⅵ脳神経(外転神経)によって神経支配を受ける[外直筋は外転神経、上斜筋は滑車神経、その他の筋(内直筋、上直筋、下直筋、下斜筋)は動眼神経によって支配される(詳細は脳科学辞典「脳神経」の項を参照)]。3つの脳幹神経核へは前庭神経核や脳幹の眼球運動関連領域からの運動指令が送られている。脳幹眼球運動関連領域のうち、内側橋延髄網様体では水平方向の眼球運動に関与する運動指令が、中脳網様体では垂直・回旋方向の眼球運動や輻輳・開散運動に関与する運動指令が生成される('''図4''')(<ref name=Kandel2022> </ref> )。5つの眼球運動や固視微動は、末梢器官や特定の脳領域からの出力信号に基づき前庭神経核や脳幹眼球運動関連領域において運動指令が生成され、その指令が脳神経を介して外眼筋へ伝えられることで生じる。 | |||
== 計測技術 == | == 計測技術 == | ||
眼球運動を測定するために、古くは直接眼球を観察することも試みられたが、視覚の時間解像度より速い眼球運動を正確に測定することは困難である(<ref name=Wade2005>'''Wade N.J., Tatler, B.W. (2005).'''<br>The Moving Tablet of the Eye. New York: Oxford University Press.</ref> )。これまでヒトや実験動物の眼球運動を計測するための様々な方法が開発され、眼球運動の詳細を解析できるようになった。研究や臨床検査などで現在使用されている主な計測方法は電気的測定法と光学的測定法に分けられる(<ref name=野城真理2011>野城真理. 3章 生体計測と神経心理学 2011. Available from: https://www.ieice-hbkb.org/files/ad_base/view_pdf.html?p=/files/S3/S3gun_10hen_03.pdf. </ref> <ref name=Hashimura2015>Hashimura M, Iizuka H, Lee J. Special Issues No.3 : Measurement Technique for Ergonomics, Section 4 : Measurements and Analyses of Bioelectric Phenomena and Others (2). The Japanese journal of ergonomics. 2015;51(6):406-10. doi: 10.5100/jje.51.406.</ref> )。 | |||
=== 電気的測定法 === | === 電気的測定法 === | ||
代表的なものは眼電図法(electro-oculogram、EOG)とサーチコイル法である。眼電図法は、眼球の角膜側がプラスに網膜側がマイナスに帯電している(この電位を角膜網膜電位とよばれる)ことを利用して、片方の目尻と鼻の付け根または両端の目尻に電極を貼り付け、2つの電極間の電位差から眼球の回転角度を求める方法である。この方法は取り扱いが容易であり、閉眼時でも計測できるので睡眠中の眼の動きを測定することが可能となる。しかし、他の方法に比べ精度は低く、信号が小さいため電磁ノイズなどの影響をうけやすい。また、回旋方向の眼球運動は測定できない。サーチコイル法は、被験者の周辺に磁場を作り、眼球にコイルを装着させることで眼の動きによってコイルが磁場を横切るときに生じる電位をもとに眼球の動きを測定する方法である。ヒトではコイルを組み込んだコンタクトレンズを装着させ、動物では強膜にコイルを慢性的に装着させるなど実験の準備にやや手間がかかるが、眼球運動の測定法では最も優れた方法である。 | |||
=== 光学的測定法 === | === 光学的測定法 === | ||
代表的なものは強膜反射法と角膜反射法である。強膜反射法は角膜と強膜で光の反射率が異なることを利用する方法で、眼球に円形の赤外光を照射した状態で眼球が動いたときの反射光量(強膜:多い、角膜:少ない)の変化をCCDカメラ等で撮影し、眼球運動を測定する。外部光の影響を受けやすいので、光が入らない状況で測定すると精度良く測定できる。一方、角膜反射法は角膜に赤外光を当てたときの反射像(プルキンエ像)が、眼球の回転中心と角膜の曲率中心の違いにより、眼球運動に伴って平行に移動することをCCDカメラ等で検出し、眼球運動を測定する。この方法では頭部の動きやカメラのずれによって測定誤差が生じるため、角膜反射法と同じ原理で瞳孔の中心も同時に検出することで測定誤差を少なくする瞳孔-角膜反射法もある。 | |||
==関連項目== | ==関連項目== | ||
* [[前庭動眼反射]] | * [[前庭動眼反射]] | ||
| 70行目: | 46行目: | ||
* [[追跡眼球運動]] | * [[追跡眼球運動]] | ||
* [[輻輳開散運動]] | * [[輻輳開散運動]] | ||
==参考文献== | ==参考文献== | ||
<references/> | <references/> | ||
2023年5月25日 (木) 20:07時点における版
眼球運動は、ほぼ球体の眼球が眼窩内で回転軸を中心に回転する運動である。その運動は、眼球に付着し、互いに拮抗する3対(上直筋-下直筋、外直筋-内直筋、上斜筋―下斜筋、計6本、左右の眼で12本)の外眼筋を収縮、弛緩させることにより遂行される。眼球運動によって視覚対象へ視線を向けるまたは保持することが可能となり、視覚を適切に働かせることができる。眼球運動には、前庭動眼反射、視運動正反応、衝動性眼球運動(サッケード)、追跡眼球運動、輻輳・開散運動、固視微動など様式や機能の異なるものがある。
特徴
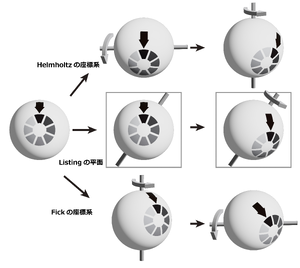
文献[1][2]を参考に作成。
眼球の位置(眼位)は慣例的に、正面を向いて視覚対象が中心窩に投影される位置に眼を向けているときを第一眼位(primary position)、視線が第一眼位から水平または垂直のみに向けられるときを第二眼位(secondary position)、それ以外の方向へ向けられたときを第三眼位(tertiary position)と定義される[3]。眼球運動は、互いに直交する3つの回転軸(水平、垂直、回旋)を中心に生じる回転運動であるため、第三眼位(つまり、斜め方向へ)へ眼を向ける際に、回転する順序によって視線移動後の回旋眼位は異なると考えられる。つまり、第三眼位への視線移動の際、例えば、水平軸を中心に回転した後、垂直軸を中心に回転する場合(Helmholtzの座標系と呼ばれる)と垂直軸を中心に回転した後、水平軸を中心に回転した場合(Fickの座標系と呼ばれる)では回旋眼位が異なる(図1)。しかし、実際には、第三眼位への視線移動はどの順序で行われたかに関係なく眼球は眼窩内で一定の位置を向いているため、第三眼位は第一眼位から1回の回転で到達する眼位とみなすことができる。
これはオランダの眼科医であるDondersが提唱し(Dondersの法則)、ドイツの数学者であるListingが数学的に定義した[1][2]。特に、Listingが述べた内容は「Listingの法則」と呼ばれ、視線移動は第一眼位の方向に直交する平面(Listingの平面)内にある軸を中心に1回転することで全ての眼位に到達すると考えられている(図1)。そのため、三次元の眼球運動は水平成分と垂直成分のみで表現できる(別の言い方をすれば、「振幅」と「方向」で表すことができる)[4]。
役割
眼球運動の目的は視覚を適切に機能させることであり、その目的から眼球運動は2つの役割に大別される。一つは体(特に頭部)が動いている最中または周りがゆっくり動いている最中に視線の方向を視覚対象へ安定に保つこと(視線保持、gaze holding)であり、もう一つは視覚対象に中心窩を向けること(中心窩視、foveation)である([3][5] )。運動時に眼を固定した状態では体(頭部)の動きに合わせて視線も動いてしまうため、視覚像がブレてしまいはっきりと見ることができない。しかし、我々は周りの風景を楽しみながら散歩したり、飛んでくるボールを見ながら落下地点まで走ったりすることができる。これは頭部の動きに合わせて眼が動くため、それにより運動時でも視線を保つことができる。また、光を受容する視細胞は網膜に均等には分布しておらず、特に視覚対象の認識に関与する錐体は中心窩に密集している。従って、中心窩から外れたところにある視覚対象を認識するためには、眼を動かせて中心窩をその対象に向ける必要がある。視線保持に関与する眼球運動は反射であり、中心窩視に関与する眼球運動は随意運動(無意識でも生じる場合がある)である。
機能に基づく分類
眼球運動は両眼が同じ方向へ動く共同性眼球運動と反対方向へ動く非共同性眼球運動に分かれる。下記の眼球運動のうち、1-4は共同性眼球運動、5は非共同性眼球運動である。また、前述の眼球運動の役割のうち、1-2は視線保持に関与し3-5は中心窩視に関与する。
- 前庭動眼反射(前庭眼反射)vestibulo-ocular reflex (VOR)(図2-1)
頭部が動いたときにこの動きと反対方向に眼球を動かすことで網膜に映る外界の像のブレを防ぐ反射(詳細は脳科学辞典「前庭動眼反射」の項を参照)。 - 視運動性反応(視機性眼球反応)optokinetic response (OKR)(図2-2)
まわりの視野がゆっくり動く時に、網膜に映る外界の像がブレないように周りと同じ方向に眼が動く反射(詳細は脳科学辞典「視運動性眼振」の項を参照)。 - 衝動性眼球運動(サッケード)saccade(図2-3)
中心窩視を得るために生じるすばやい眼球運動で、眼球速度は最大1000°/s-1 にまで達する。VORやOKRによる目の動きをリセットするすばやい目の動き(急速相)から生じたとされている([3][5] )。 - 追跡眼球運動(滑動性追跡眼球運動) pursuit eye movement (smooth pursuit)(図2-4)
ゆっくり動く視覚対象物の網膜像を網膜中心窩付近に維持し、その動きに合わせて視線を滑らかに動かす眼球運動(詳細は脳科学辞典「追跡眼球運動」の項を参照)。 - 輻輳・開散運動 vergence (convergence・divergence)(図2-5)
観察者から異なる距離(奥行き)にある対象物に視線を移動させた時に起こる両眼が違う方向に動く眼球運動。輻輳は視覚対象が遠位から近づくとき、開散は近位から遠ざかるときの眼球運動をいう。(詳細は脳科学辞典「輻輳開散運動」の項を参照)。
-
図2-1. 前庭動眼反射の時の眼の動き
頭部の動きと逆向きに眼が動く。 -
図2-2. 視運動性反応の時の眼の動き
周囲の動きと同じ方向に眼が動く。 -
図2-3. サッケードの時の眼の動き
眼がすばやく動く。 -
図2-4. 追跡眼球運動の時の眼の動き
標的の動きと同じ速さで目が動く。 -
図2-5. 輻輳・開散時の眼の動き
左右の眼がそれぞれ異なる方向へ動く。
上記の5つの眼球運動に加えて、固視微動 fixation nystagmus, fixation eye movementという眼球運動もみられる([6] )。前述の通り、視覚対象に視線を一定に保つことで視覚認識が行われるが、視線が全く動かないと、時間と共に視覚刺激に対し反応しにくくなる([7] )。固視微動は不随意的な眼球運動で、網膜像を絶えず変化させることによって視覚入力を絶えず生成する役割がある。固視微動は眼球速度によってトレモア(tremor)、ドリフト(drift)、マイクロサッケード(microsaccade)の3種類ある(詳細は脳科学辞典「マイクロサッケード」の項を参照)。
神経経路

カンデル神経科学第2版 図35-1((株)メディカル・サイエンス・インターナショナルからの転載許可を得て掲載)。
カンデル神経科学第2版 図35-3((株)メディカル・サイエンス・インターナショナルからの転載許可を得て掲載)。
眼球に付着する6本の外眼筋(図3)([8] )は脳幹の動眼神経核、滑車神経核、外転神経核を起始核とする第Ⅲ脳神経(動眼神経)、第Ⅳ脳神経(滑車神経)、第Ⅵ脳神経(外転神経)によって神経支配を受ける[外直筋は外転神経、上斜筋は滑車神経、その他の筋(内直筋、上直筋、下直筋、下斜筋)は動眼神経によって支配される(詳細は脳科学辞典「脳神経」の項を参照)]。3つの脳幹神経核へは前庭神経核や脳幹の眼球運動関連領域からの運動指令が送られている。脳幹眼球運動関連領域のうち、内側橋延髄網様体では水平方向の眼球運動に関与する運動指令が、中脳網様体では垂直・回旋方向の眼球運動や輻輳・開散運動に関与する運動指令が生成される(図4)([8] )。5つの眼球運動や固視微動は、末梢器官や特定の脳領域からの出力信号に基づき前庭神経核や脳幹眼球運動関連領域において運動指令が生成され、その指令が脳神経を介して外眼筋へ伝えられることで生じる。
計測技術
眼球運動を測定するために、古くは直接眼球を観察することも試みられたが、視覚の時間解像度より速い眼球運動を正確に測定することは困難である([9] )。これまでヒトや実験動物の眼球運動を計測するための様々な方法が開発され、眼球運動の詳細を解析できるようになった。研究や臨床検査などで現在使用されている主な計測方法は電気的測定法と光学的測定法に分けられる([10] [11] )。
電気的測定法
代表的なものは眼電図法(electro-oculogram、EOG)とサーチコイル法である。眼電図法は、眼球の角膜側がプラスに網膜側がマイナスに帯電している(この電位を角膜網膜電位とよばれる)ことを利用して、片方の目尻と鼻の付け根または両端の目尻に電極を貼り付け、2つの電極間の電位差から眼球の回転角度を求める方法である。この方法は取り扱いが容易であり、閉眼時でも計測できるので睡眠中の眼の動きを測定することが可能となる。しかし、他の方法に比べ精度は低く、信号が小さいため電磁ノイズなどの影響をうけやすい。また、回旋方向の眼球運動は測定できない。サーチコイル法は、被験者の周辺に磁場を作り、眼球にコイルを装着させることで眼の動きによってコイルが磁場を横切るときに生じる電位をもとに眼球の動きを測定する方法である。ヒトではコイルを組み込んだコンタクトレンズを装着させ、動物では強膜にコイルを慢性的に装着させるなど実験の準備にやや手間がかかるが、眼球運動の測定法では最も優れた方法である。
光学的測定法
代表的なものは強膜反射法と角膜反射法である。強膜反射法は角膜と強膜で光の反射率が異なることを利用する方法で、眼球に円形の赤外光を照射した状態で眼球が動いたときの反射光量(強膜:多い、角膜:少ない)の変化をCCDカメラ等で撮影し、眼球運動を測定する。外部光の影響を受けやすいので、光が入らない状況で測定すると精度良く測定できる。一方、角膜反射法は角膜に赤外光を当てたときの反射像(プルキンエ像)が、眼球の回転中心と角膜の曲率中心の違いにより、眼球運動に伴って平行に移動することをCCDカメラ等で検出し、眼球運動を測定する。この方法では頭部の動きやカメラのずれによって測定誤差が生じるため、角膜反射法と同じ原理で瞳孔の中心も同時に検出することで測定誤差を少なくする瞳孔-角膜反射法もある。
関連項目
参考文献
- ↑ 1.0 1.1 鈴木康夫 (1997).
なぜ今 Listingの法則なのか?. Equilibrium Research. 56(5):401-12. - ↑ 2.0 2.1 鈴木康夫 (2017).
回転として眼球運動を考えよう! Listingの法則とは?. 神経眼科. 34(2):139-47. - ↑ 3.0 3.1 3.2 Carpenter R.H.S. (1988).
Movements of eyes (2nd edn): Pion Press, London. - ↑ フィンドレイ JM, ギルクリスト, I.D., 本田仁視(監訳)(2006).
アクティブ・ビジョン 眼球運動の心理・神経科学: 北大路書房. - ↑ 5.0 5.1 Leigh RJ, Zee, D.S. (2015).
The Neurology of Eye Movements (5th ed): Oxford University Press. - ↑
Martinez-Conde, S., & Macknik, S.L. (2007).
Windows on the mind. Scientific American, 297(2), 56-63. [PubMed:17894173] [WorldCat] [DOI] - ↑
PRITCHARD, R.M. (1961).
Stabilized images on the retina. Scientific American, 204, 72-8. [PubMed:13738093] [WorldCat] [DOI] - ↑ 8.0 8.1 Kandel E.R., Koester J., Mack S., Siegelbaum S., 宮下 保, 岡野 栄, et al. (2022).
カンデル神経科学. 第2版 ed: メディカル・サイエンス・インターナショナル xlviii, 1653p p. - ↑ Wade N.J., Tatler, B.W. (2005).
The Moving Tablet of the Eye. New York: Oxford University Press. - ↑ 野城真理. 3章 生体計測と神経心理学 2011. Available from: https://www.ieice-hbkb.org/files/ad_base/view_pdf.html?p=/files/S3/S3gun_10hen_03.pdf.
- ↑ Hashimura M, Iizuka H, Lee J. Special Issues No.3 : Measurement Technique for Ergonomics, Section 4 : Measurements and Analyses of Bioelectric Phenomena and Others (2). The Japanese journal of ergonomics. 2015;51(6):406-10. doi: 10.5100/jje.51.406.