(3人の利用者による、間の51版が非表示) 1行目:
1行目: <div align="right">
英語名:Michaelis-Menten plot
<font size="+1">[http://researchmap.jp/read0018043 石田 敦彦]</font><br>
''広島大学 大学院統合生命科学研究科''<br>
DOI:<selfdoi /> 原稿受付日:2012年8月29日 原稿完成日:2012年9月10日 一部改訂:2021年8月28日<br>
担当編集委員:[http://researchmap.jp/2rikenbsi 林 康紀](京都大学大学院医学研究科)<br>
</div>
英語名:Michaelis-Menten equation 独:Michaelis-Menten-Gleichnung 仏:Équation de Michaelis-Menten
同義語: S -vプロット、ミカエリス・メンテンの式、ブリッグス・ホールデンの式
同義語: ミハエリス・メンテンの式、ミヒャエリス・メンテンの式
== ミカエリス・メンテンの式 ==
{{box|text=
[[wikipedia:ja:レオノール・ミカエリス|L. Michaelis]] と[[wikipedia:ja:モード・メンテン |M. L. Menten]]は[ [wikipedia:ja:インベルターゼ|インベルターゼ]]に関する研究において、[[wikipedia:ja:酵素|酵素]]の反応速度と[[wikipedia:ja:基質|基質]]濃度の関係を明らかにするため、酵素と基質が結合した酵素基質複合体(ES complex)を形成することにより[[wikipedia:ja:酵素反応|酵素反応] ]が進行するとの概念に基づいて、次のような反応スキームを考えた。
酵素の反応速度<math>v</math>(酵素活性)と基質濃度<math>[S]</math>の関係を示す酵素反応速度論の基本式で、
::<math>v = \frac{V_{max}[S]}{K_m +[S]}</math>
<math> E + S \overset {k_1} {\underset{k_2}{\rightleftarrows }} ES \xrightarrow {k_3} E + P </math> (1)
で表される。<math>K_m</math>はミカエリス定数と呼ばれ、最大反応速度<math>V_{max}</math>の1/2を与える基質濃度に相当する。<math>K_m</math>は酵素基質複合体における酵素と基質の親和性の尺度であり、<math>K_m</math>値が小さいほど酵素と基質の親和性が高いことを示す。酵素の化学的実体が未だ明確にされてはいなかった1913年にL. Michaelis とM. L. Mentenによって導かれたが、この方法は酵素基質複合体が迅速に形成され、尚且つ結合と解離の平衡状態にあることなどを仮定したものであったので、1925年にG. E. BriggsとJ. B. S. Haldaneが、定常状態近似と呼ばれる、より一般化された仮定を用いて同じ式を導出した。<math>K_m</math>の定義が異なっているので、両者は厳密には別の式であるが、形式が全く同じであるので、実際には混同して用いられることが多い。この式を基礎として数理モデルを構築し、実際の酵素活性の測定データをそのモデルに合わせて解析することにより、他の手法では得ることが難しい酵素反応機構や酵素阻害剤の作用機構に関する重要な情報を、比較的簡便に得ることができる。}}
ここに <math>E</math>は酵素、<math>S</math>は基質、<math>P </math>は生成物を表す。この時、 <math>K_1 </math>、<math>K_2< /math>は <math>K_3 </math>に比べて十分に大きく、 <math>ES </math>、<math> E</math>、<math> S</math>は[[wikipedia:ja:平衡状態|平衡状態]]にあって、<math>K_3</math>を[[wikipedia:ja:速度定数|速度定数]]とする過程が全体の酵素反応の[[wikipedia:ja:律速段階|律速段階]]であると仮定すれば、ES complexの[[wikipedia:ja:解離定数|解離平衡定数]] <math>K_d </math>は
==背景==
酵素は生体内の各種の化学反応を円滑に行わせるための生体触媒であり、脳内においても情報伝達や物質代謝など、あらゆる生化学反応に関わっている。そのため生体を理解する上で、個々の酵素の性質を明らかにすることは極めて重要である。1992年に[[ジーンターゲティング]]の手法を用いて、[[空間記憶]]に関わる酵素として[[CaMキナーゼⅡ]]が初めて特定された<ref><pubmed>1378648</pubmed></ref><ref><pubmed>1321493</pubmed></ref>が、この輝かしい研究成果も、それを遡ること十数年に渡る本酵素に関する地道で精力的な研究の積み重ね<ref><pubmed>12045104</pubmed></ref>があったればこそのものであろう。
酵素の生化学的研究をおこなうにあたっては、酵素の性質を定量的に扱うことが大前提となる。その理論的基盤となるものが、1913年に[[wj:レオノール・ミカエリス|L. Michaelis]]と[[wj:モード・メンテン|M. L. Menten]]によって[[wj:インベルターゼ|インベルターゼ]]に関する研究において導かれたミカエリス・メンテンの式である<ref name=Michaelis1913><pubmed>21888353</pubmed></ref>。この式は、以下に詳述するように、酵素基質複合体が迅速に形成され、尚且つ結合と解離の平衡状態にあることなどを仮定した反応モデルに基づいて導かれたものであるが、発表当時は酵素の化学的実体が未だ明確にされてはいなかった時代であった。そのような時代に数理モデルに基づいて式が確立され、それが 100年以上たった今日でも未だ各方面で利用されているというのは、理論よりも実験が先行する生化学分野においては極めて珍しい例ではなかろうか。ちなみにMentenは当時としては珍しい女性研究者である<ref>'''鈴木紘一、笠井献一、宗川吉汪 監訳 (2008).'''<br>ホートン生化学 第4版 ''東京化学同人 (東京)''</ref>。さらに1925年に[[w:George Edward Briggs|G. E. Briggs]]と[[wj:J・B・S・ホールデン|J. B. S. Haldane]]が、定常状態近似と呼ばれる、より一般化された仮定を用いて同じ式を導出した<ref name=Briggs1925><pubmed>16743508</pubmed></ref>。<math>K_m</math>の定義が異なっているので、両者は厳密には別の式であるが、形式が全く同じであるので、実際には混同して用いられることが多い。
<math> K_d = \frac{ [E][S]}{[ES ]} = \frac{k_2}{k_1} </math> (2)
==誘導法==
MichaelisとMentenは[[wj:酵素|酵素]]の反応速度と[[wj:基質|基質]]濃度の関係を明らかにするため、酵素と基質が結合した酵素基質複合体(ES complex)を形成することにより[[wj:酵素反応|酵素反応]]が進行するとの概念に基づいて、次のような反応スキームを考えた。
<math> E + S \overset{k_1}{\underset{k_2}{\rightleftarrows}} ES \xrightarrow{k_3} E + P</math> (1)
酵素反応の初速度 <math>v </math>は
ここに<math>E</math>は酵素、<math>S</math>は基質、<math>P</math>は生成物を表す。この時、<math>k_1</math>、<math>k_2</math>は<math>k_3</math>に比べて十分に大きく、<math>ES</math>、<math>E</math>、<math>S</math>は[[wj:平衡状態|平衡状態]]にあって、<math>k_3</math>を[[wj:速度定数|速度定数]]とする過程が全体の酵素反応の[[wj:律速段階|律速段階]]であると仮定すれば、ES complexの[[wj:解離定数|解離平衡定数]]<math>K_d</math>は
<br> <math> K_d = \frac{[E][S]}{[ES]} = \frac{k_2}{k_1}</math> (2)
<math>v = k_3 [ES]\, </math> (3 )
<br> 酵素反応の初速度<math>v</math>は
<br> <math>v = k_3[ES]\,</math> (3)
ここで酵素の全濃度 <math>[E_0 ]</math>は
<br> ここで酵素の全濃度<math>[E]_0</math>は
<br> <math>[E]_0 = [E] + [ES]\,</math> (4)
<math>[E_0 ] = [E] + [ES]\,</math> (4)
<br> (2)(4)より<math>[E]</math>を消去して整理すると
<br> <math> [ES] = \frac{[E]_0[S]}{K_d +[S]}</math> (5)
(2)(4)より <math>[E]</math>を消去して整理すると
<br> これを(3)に代入すれば
<br> <math> v = k_3[ES] = \frac{k_3[E]_0[S]}{K_d +[S]}</math> (6)
<math> [ES] = \frac{[E_0 ][S]}{K_d +[S]}</math> (5 )
<br> ここで<math>v = k_3[E]_0 = V_{max}</math>、<math>K_d = K_m</math>とおくと
<br> <math>v = k_3[ES] = \frac{V_{max}[S]}{K_m +[S]}</math> (7)
これを (3 )に代入すれば
この(7)式をミカエリス・メンテンの式と呼び、1913年にドイツの学術雑誌に発表された<ref name=Michaelis1913><pubmed>21888353</pubmed></ref>。ミカエリス定数<math>K_m</math>は基質濃度無限大の時の最大反応速度<math>V_{max}</math>の1/2の速度を与える時の基質濃度に一致する。<math>K_m</math>はES complexの解離平衡定数<math>K_d</math>であるから、酵素と基質の親和性の尺度となり、値が小さいほど酵素と基質の親和性が強い。
== ブリッグス・ホールデンの式 ==
<math> v = k_3[ES] = \frac{k_3[E_0][S]}{K_d +[S]}</math> (6)
しかしながら、上記、Michaelis とMentenの考えではいくつかの仮定を設けており、常にこれらの仮定が成立するとは限らない。そこで1925年に[[w:George Edward Briggs|G. E. Briggs]]と[[wj:J・B・S・ホールデン|J. B. S. Haldane]]は、ミカエリス・メンテンの式の、より一般化された誘導法を示した<ref name=Briggs1925><pubmed>16743508</pubmed></ref>。上記(1)の反応スキームにおいて、彼らは酵素反応が直線的に進行する定常状態ではES complexの形成速度と分解速度が釣り合っていて、見かけ上<math>[ES]</math>が一定になると仮定した(定常状態近似)。すなわち、 '''
<br> <math>\frac{d[ES]}{dt} = 0 = k_1[E][S] - k_2[ES] -k_3[ES]</math> (8)
ここで <math> v = k_3 [E_0 ] =V_ {max }</math>、<math> k_d = k_m </math>とおくと
<br> ここで上記と同様に酵素の全濃度<math>[E]_0</math>は
<br> <math>[E]_0= [E] + [ES]\,</math> (9)
<math>v = k_3 [ES ] = \frac{V_{max} [S ]}{K_m +[S ]} </math> (7 )
<br> (8)(9)より<math>[E]</math>を消去すると
この(7)式をミカエリス・メンテンの式と呼び、1913年にドイツの学術雑誌に発表された<ref><pubmed>21888353</pubmed></ref>。ちなみにM. L. Mentenは当時としては珍しい女性研究者である<ref>''' 鈴木紘一、笠井献一、宗川吉汪 監訳<br>ホートン生化学 第4版 <br>''東京化学同人 (東京)'':2008</ref>。ミカエリス定数<math>K_m</math>は基質濃度無限大の時の最大反応速度<math>V_{max}</math>の1/2の速度を与える時の基質濃度に一致する。<math>K_m</math>はES complexの解離平衡定数 <math>K_d </math>であるから、酵素と基質の親和性の尺度となり、値が小さいほど酵素と基質の親和性が強い。
<math>[ES] = \frac{k_1[E]_0[S]}{k_1[S]+(k_2 + k_3)}</math> (10)
== ブリッグス・ホールデンの式 ==
<br> 酵素反応の初速度<math>v</math>は
しかしながら、上記、Michaelis とMentenの考えではいくつかの仮定を設けており、常にこれらの仮定が成立するとは限らない。そこで1925年に[[wikipedia:George Edward Briggs|G. E. Briggs]]と[[wikipedia:ja:J・B・S・ホールデン|J. B. S. Haldane]]は、ミカエリス・メンテンの式の、より一般化された誘導法を示した <ref ><pubmed>16743508</pubmed></ref>。上記(1)の反応スキームにおいて、彼らは酵素反応が直線的に進行する定常状態ではES complexの形成速度と分解速度が釣り合っていて、見かけ上 <math>[ES] </math>が一定になると仮定した(定常状態近似)。すなわち、
<br> <math>v=k_3[ES]\,</math> (11)
<br> (10)(11)より
<math >\frac{d[ES]}{dt} = 0 = k_1[E][S] - k_2[ES] -k_3[ES]</math> (8 )
<br> <math>v = \frac{k_1k_3[E]_0[S]}{k_1[S]+(k_2 + k_3)} = \frac{k_3[E]_0[S]}{[S]+\frac{k_2 + k_3}{k_1}}</math> (12)
<br> ここで <math>(k_2+k_3) / k_1 = K_m</math>、<math>k_3[E]_0 = V_{max}</math>とおくと
ここで上記と同様に酵素の全濃度 <math>[E_0 ]</math>は
<br> <math>v = k_3[ES] = \frac{V_{max}[S]}{K_m +[S]}</math> (13)
<br> となり、(7)式と同じ式が得られる。 (13)式は厳密にはブリッグス・ホールデンの式と言うが、 (7)式と同じ形であるので実際にはミカエリス・メンテンの式と言うことが多い。また、(13)式の<math>K_m</math>もミカエリス定数と言うが、(7)式の場合と異なり、ES complexの解離平衡定数<math>K_d</math>とは一致しない。<math>k_2>>k_3</math>の場合にのみ、<math>K_m\approx k_2/k_1</math>となって<math>K_d</math>と一致するのであるが、多くの場合、(13)式の<math>K_m</math>も酵素と基質の親和性の尺度を表すと考えてよい。実験的には、(13)式の<math>K_m</math>も(7)式の場合と同様、基質濃度無限大の時の最大反応速度<math>V_{max}</math>の1/2の速度を与える基質濃度として定義される。
<math>[E_0]= [E] + [ES] \, </math> (9 )
== ミカエリス・メンテンプロット ==
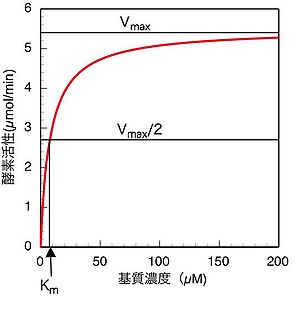
[[Image:Atsuhikoishida fig 1.jpg|thumb|300px|<b>図1.基質濃度と酵素活性の関係</b><br>(ミカエリス・メンテンプロット、またはS-vプロット)]]
(8)(9)より <span class="texhtml" >[''E''] </span >を消去すると
(7)式も(13)式も、酵素反応速度(すなわち酵素活性)と基質濃度の関係を定量的に表した式である。実験的には様々な基質濃度で酵素活性を測定し、横軸に基質濃度、縦軸に酵素活性をとってプロットした場合、'''図1'''に示すように、数学的には[[wj:直角双曲線|直角双曲線]]の形となる。このようなプロットをミカエリス・メンテンプロット(S-vプロット)と呼ぶ。'''図1'''から明らかなように、基質濃度が<math>K_m</math>値(<math>V_{max}</math>の1/2の速度を与える時の基質濃度)付近或いはそれ以下の場合には酵素活性は基質濃度に大きく依存し、基質濃度の少しの変化でも酵素活性は大きく影響を受けるが、<math>K_m</math>値より十分大きい基質濃度の場合、酵素活性は<math>V_{max}</math>の値に近づき、濃度が大きくなるにつれて基質濃度依存性が殆どなくなる。従って、一般に酵素活性を測定する場合は、基質初濃度の誤差や、反応の進行に伴う基質濃度減少の影響を避けるため、できるだけ高濃度の基質(<math>K_m</math>値の5〜10倍、或いはそれ以上)を用いて活性測定を行うことが望ましい。しかしながら基質阻害により、高濃度では逆に活性が低下する場合もあるので、基質濃度を予め低濃度から高濃度まで振ってみて基質阻害がないことを確認するなどの注意も必要である。
<math> [ES] = \frac{k_1 [E_0 ][S ]}{k_1[S]+(k_2 + k_3) }</math> (10 )
== 速度論的パラメータの求め方 ==
'''図1'''のようなミカエリス・メンテンプロットより、上記<math>K_m</math>や<math>V_{max}</math>などの速度論的パラメータを求めることが出来る。(7)式または(13)式の両辺の逆数をとって
酵素反応の初速度<span class="texhtml"> ''v ''</span >は
<br> <math>\frac{1}{v} = \frac{K_m}{V_{max}}\frac{1}{[S]} + \frac{1}{V_{max}}</math> (14)
<br> とすれば、<math>1 / [S]</math>に対する<math>1 / v</math>のプロットが直線となる。従ってミカエリス・メンテンの式に従う酵素では、基質濃度の逆数に対して、酵素活性の逆数をプロットすれば'''図2'''に示すような直線プロット(ラインウィーバー・バークプロットまたは二重逆数プロット)となり、このプロットの<math>x</math>切片が<math>-1/Km</math>、<math>y</math>切片が<math>1 / V_{max}</math>を与える。この方法はグラフ用紙さえあれば簡単にできるので以前はよく行われたが、低基質濃度のデータの誤差が大きく出るなどの欠点もあり、パソコンが普及した現在では、ミカエリス・メンテンプロットを適当なソフトウェアを用いて双曲線にフィッティングして、直接(7)式または(13)式の各パラメータを求めるdirect fitting法によることが多くなった。
<math>v=k_3 [ES ]\, </math> (11 )
[[Image:AtsuhikoIshida fig 2.jpg|thumb|300px|''''''図2'''. ラインウィーバー・バークプロット(二重逆数プロット)''']] <br> (7)式または(13)式(ミカエリス・メンテンの式またはブリッグス・ホールデンの式)は多くの酵素にあてはまる便利な式であるが、(1)の反応スキームに従うことを前提にしているので、当然これにあてはまらない場合も存在する。そのような場合に(7)式または(13)式を無理にあてはめて解析することは、誤った結論を導く可能性があるので注意が必要である。そのような場合の扱いに関しては、例えば以下の文献を参照されたい<ref>''' 堀尾武一、山下仁平 (1981).'''<br>蛋白質・酵素の基礎実験法, ''南江堂 (東京)''</ref>。
== 速度論的パラメータの意味 ==
(10)(11)より
前にも述べたように、<math>K_m</math>は<math>V_{max}</math>の1/2の速度を与える時の基質濃度として定義され、酵素と基質の親和性の尺度となる。また、<math>V_{max}</math>は基質濃度無限大、つまり酵素分子全てが基質で飽和された時の反応速度である。定義により、<math>V_{max}=k_3[E]_0</math>であるが、この<math>k_3</math>を[[触媒定数]]、或いはターンオーバー・ナンバーと呼び、通常<math>k_{cat}</math>で表す。すなわち
<br> <math>k_{cat} = \frac{V_{max}}{[E]_0}</math> (15)
<math>v = \frac {k_1k_3[E_0][S]}{k_1[S]+(k_2 + k_3) } = \frac{k_3[E_0][S] }{[S ]+\frac{k_2 + k_3}{k_1} }</math> (12 )
<br> である(<math>[E]_0</math>は全酵素濃度)。<math>k_{cat}</math>は酵素が基質で飽和された状態において、1モルの酵素(或いは活性部位)が1秒間に生成物へ変換できる基質のモル数を表し、単位は<math>s^{-1}</math>である。すなわち<math>k_{cat}</math>は酵素の触媒効率を表す指標である。また、(7)または(13)式の<math>V_{max}</math>を(15)式により、<math>k_{cat}[E]_0</math>で置き換えると
<br> <math>v = k_3[ES] = \frac{k_{cat}[E]_0[S]}{K_m +[S]}</math> (16)
ここで <math>(k_2+ k_3) / k_1= K_m</math >、 <math>k_3[E_0 ] = V_ {max }</math>とおくと
<br> ここで基質濃度が非常に希薄な<math>[S] << K_m</math>の濃度領域を考えると
<br> <math>v = \frac{k_{cat}[E]_0[S]}{K_m +[S]} \approx \frac{k_{cat}[E]_0[S]}{K_m} = \frac{k_{cat}}{K_m}[E]_0[S]</math> (17)
<math>v = k_3[ES] = \frac{V_ {max }[S]}{K_m +[S]}</math> (13 )
<br> 基質が非常に薄い条件下では、基質は殆ど酵素に結合していないと考えられるから<math>[E]_0\approx[E]</math>
従って
<br> <math>v = \frac{k_{cat}}{K_m}[E][S]</math> (18)
となり、(7)式と同じ式が得られる。 (13)式は厳密にはブリッグス・ホールデンの式と言うが、 (7)式と同じ形であるので実際にはミカエリス・メンテンの式と言うことが多い。また、(13)式の<math>K_m</math>もミカエリス定数と言うが、(7)式の場合と異なり、ES complexの解離平衡定数<math>K_d</math>とは一致しない。<math>K_2>>K_3</math>の場合にのみ、<math>K_m</math>≈<math>k_2 </math >/ <math>k_1</math>となって<math>K_d</math>と一致するのであるが、多くの場合、(13)式の<span class ="texhtml">''K''<sub>''m''</sub></span>も酵素と基質の親和性の尺度を表すと考えてよい。実験的には、(13)式の<math> K_m</math>も (7 )式の場合と同様、基質濃度無限大の時の最大反応速度<math>V_max</math>の1/2の速度を与える基質濃度として定義される。
<br> この式は<math>E</math>と<math>S</math>の衝突が反応全体の速度を支配していると考えた場合の二次反応速度定数が<math>k_{cat}/K_m</math>であることを示している。<math>k_{cat}/K_m</math>の値は、異なる酵素の触媒効率を比較する際のパラメータとして用いられる。また、同一の酵素に対して、異なる基質の特異性を議論する場合にも<math>k_{cat}/K_m</math>の値が用いられ、特異性定数と呼ばれることがある。この場合、<math>k_{cat}/K_m</math>の値が大きいほど、その酵素に対してよい基質であるということになる。
== ミカエリス・メンテンプロット ==
== 阻害剤存在下の酵素反応速度論 ==
[[Image:Atsuhikoishida fig 1.jpg|thumb|300px|'''図.基質濃度と酵素活性の関係'''(ミカエリス・メンテンプロット、またはS-vプロット)]]
酵素の特異的阻害剤は、その酵素の生理的意義を明らかにする分子プローブとして重要であるのみならず、医薬品として臨床上、重要な役割を担うものも多い。ミカエリス・メンテンの式を応用して様々な濃度の酵素阻害剤存在下での酵素活性を詳細に調べることにより、阻害剤と酵素の結合様式や結合親和性について重要な情報を得ることが出来る。
(7)式も(13)式も、酵素反応速度(すなわち酵素活性)と基質濃度の関係を定量的に表した式である。実験的には様々な基質濃度で酵素活性を測定し、横軸に基質濃度、縦軸に酵素活性をとってプロットした場合、図に示すように、数学的には[[wikipedia:ja:直角双曲線|直角双曲線]]の形となる。このようなプロットをミカエリス・メンテンプロット(S-vプロット)と呼ぶ。図から明らかなように、基質濃度が<span class="texhtml">''K''<sub>''m''</sub></span>値(<span class="texhtml">''V''<sub>''max''</sub></span>の1/2の速度を与える時の基質濃度)付近或いはそれ以下の場合には酵素活性は基質濃度に大きく依存し、基質濃度の少しの変化でも酵素活性は大きく影響を受けるが、<span class="texhtml">''K''<sub>''m''</sub></span>値より十分大きい基質濃度の場合、酵素活性は<span class="texhtml">''V''<sub>''max''</sub></span>の値に近づき、濃度が大きくなるにつれて基質濃度依存性が殆どなくなる。従って、一般に酵素活性を測定する場合は、基質初濃度の誤差や、反応の進行に伴う基質濃度減少の影響を避けるため、基質阻害などの問題がない限りは、できるだけ高濃度の基質(<span class="texhtml">''K''<sub>''m''</sub></span>値の5〜10倍、或いはそれ以上)を用いて活性測定を行うことが望ましい。
<br>
== 速度論的パラメータの求め方 ==
=== 競合阻害===
(1)の反応スキームにおいて阻害剤<math>I</math>が酵素の基質結合部位に結合し、基質Sと阻害剤<math>I</math>が結合部位を奪い合うような場合を競合阻害(拮抗阻害:competitive inhibition)と呼ぶ。この場合、(1)の反応スキームに加えて
図1のようなミカエリス・メンテンプロットより、上記<span class="texhtml">''K''<sub>''m'' </sub ></span>や<span class="texhtml" >''V'' <sub >''max'' </sub ></span>などの速度論的パラメータを求めることが出来る。以前は(7)式または (13 )式の両辺の逆数をとって
<br> <math>E + I {\rightleftarrows} EI</math> (19)
<math>\frac{1}{v} = \frac{K_m}{V_{max}}\frac{1}{[S]} + \frac{1}{V_ {max} }</math> (14 )
という結合解離平衡を仮定し、その解離定数を<math>K_i</math>とおくと
とし、1/[S]に対して1/vをプロットして得られる直線プロット([[ラインウィーバー・バークプロット]])のx切片及びy切片より<math>K_m</math>や <math>V_{max} </math>を求める方法がよく行われたが、最近はパソコンの普及により、ミカエリス・メンテンプロットを適当なソフトウェアを用いて双曲線にフィッティングして、直接(7)式または(13)式の各パラメータを求めるdirect fitting法によることが多くなった。
<br> <math>K_i = \frac{[E][I]}{[EI]}</math> (20)
(7)式または(13)式(ミカエリス・メンテンの式またはブリッグス・ホールデンの式)は多くの酵素にあてはまる便利な式であるが、(1)の反応スキームに従うことを前提にしているので、当然これにあてはまらない場合も存在する。そのような場合に(7)式または(13)式を無理にあてはめて解析することは、誤った結論を導く可能性があるので注意が必要である。そのような場合の扱いに関しては、例えば以下の文献を参照されたい<ref>''' 堀尾武一、山下仁平 <br>蛋白質・酵素の基礎実験法 <br >''南江堂 (東京)'':1981 </ref >。
この場合、酵素の全濃度<math>[E]_0</math>は(4)式に代わって
== 速度論的パラメータの意味 ==
<br> <math>[E]_0 = [E] + [ES] + [EI]\,</math> (21)
前にも述べたように、 <span class="texhtml">''K''<sub>''m''</sub ></span>は<span class="texhtml">''V''<sub>''max''</sub></span>の1/2の速度を与える時の基質濃度として定義され、酵素と基質の親和性の尺度となる。また、<span class="texhtml">''V''<sub>''max''</sub></span>は基質濃度無限大、つまり酵素分子全てが基質で飽和された時の反応速度である。定義により、<span class="texhtml">''V''<sub>''max''</sub> = ''k''<sub>3</sub >['' E''<sub>0</sub> ]</span>であるが、この<span class ="texhtml">''k''<sub>3</sub></span>を [[触媒定数 ]]、或いはターンオーバー・ナンバーと呼び、通常<span class="texhtml">''k''<sub>''cat''</sub> </span >で表す。すなわち
(2)(20)(21)より<math>[E]</math>と<math>[EI]</math>を消去して<math>[ES]</math>について整理すると
<math>k_{cat} = \frac{V_{max}}{ [E_0 ]} </math> (15)
<br> <math>[ES] = \frac{[E]_0[S]}{[S]+K_d(1+\frac{[I]}{K_i})}</math> (22)
である( <span class="texhtml">[''E''<sub >0 </sub >]</span>は全酵素濃度)。<span class ="texhtml">''k''<sub>''cat''</sub></span>は酵素が基質で飽和された状態において、1モルの酵素(或いは活性部位)が1秒間に生成物へ変換できる基質のモル数を表し、単位は<span class="texhtml">''s''<sup> − 1</sup></span>である。すなわち<span class="texhtml">''k''<sub>''cat''</sub></span>は酵素の触媒効率を表す指標である。また、(7)または (13 )式の<span class="texhtml">''V''<sub>''max'' </sub ></span>を (15 )式により、<span class="texhtml">''k''<sub>''cat''</sub>[''E''<sub>0</sub>]</span>で置き換えると
これを(3)に代入すれば
<math>v = k_3[ES] = \frac{k_{cat}[E_0][S]}{K_m +[S]}</math> (16 )
<br> <math>v = \frac{k_3[E]_0[S]}{[S]+K_d(1+\frac{[I]}{K_i})}</math> (23)
ここで基質濃度が非常に希薄な <span class="texhtml" >['' S'' ] < < ''K''<sub>''m''</sub> </span >の濃度領域を考えると
ここで <math>k_3[E]_0 = V_{max}</math>、<math>K_d=K_m</math>であるから
<math>v = \frac{k_{cat}[E_0][S]}{K_m +[S]} \approx \frac{k_{cat} [E_0 ][S]}{K_m} = \frac {k_{cat} }{ K_m}[E_0][S] </math> (17)
<br> <math>v = \frac{V_{max}[S]}{[S]+K_m(1+\frac{[I]}{K_i})}</math> (24)
基質が非常に薄い条件下では、基質は殆ど酵素に結合していないと考えられるから <math>[E_0 ] \approx [E ]</math>
この式を元のミカエリス・メンテンの式 (7)式と比較すると、競合阻害剤<math>I</math>の存在下では<math>V_{max}</math>は変化しないが、<math>K_m</math>値が<math>1 + [I] / K_i</math>倍だけ増加していることが分かる。 また、(14)式と同様に(24)式の逆数をとって整理すると
従って
<br> <math>\frac{1}{v} = \frac{K_m(1+\frac{[I]}{K_i})}{V_{max}}\frac{1}{[S]} + \frac{1}{V_{max}}</math> (25)
従って<math>1 / [S]</math>に対して<math>1 / v</math>をプロット(ラインウィーバー・バークプロットまたは二重逆数プロット)すると'''図3'''のような直線プロットとなり、様々な濃度の阻害剤<math>I</math>の存在下で実験すると、y軸上の一点(<math>y</math>切片 <math>= 1 / V_{max}</math>)で交わる直線群が得られる。
[[Image:AtsuhikoIshida fig 3.jpg|thumb|300px|'''図3.競合阻害剤存在下でのラインウィーバー・バークプロット'''<br>各直線はy軸上の一点で交わる。]]これらの直線の傾きは
<br> <math>\frac{K_m(1+\frac{[I]}{K_i})}{V_{max}} = \frac{K_m}{V_{max}}\frac{1}{K_i}[I] + \frac{K_m}{V_{max}}</math> (26)
と表せるので、各阻害剤濃度<span class="texhtml">[''I'']</span>に対して、'''図3'''のラインウィーバー・バークプロットの傾きをプロットした図4のような2次プロットを作成すると、(26)式に従った直線となり、その直線の<math>x</math>切片(<math>-K_i</math>に相当)の値から<math>K_i</math>値を求めることが出来る。<math>K_i</math>は阻害定数と呼ばれ、この場合、酵素—阻害剤複合体の解離定数に相当する。<math>K_i</math>は酵素と阻害剤の親和性の尺度であり、値が小さいほど酵素に対する親和性が強いことを示す。
[[Image:AtsuhikoIshida fig 4.jpg|thumb|300px|'''図4.Ki値を求めるための二次プロット'''<br>各阻害剤濃度に対して'''図3'''のプロットの傾きをプロットしたもの。]]
<br>
===非競合阻害===
(1)の反応スキームにおいて阻害剤<math>I</math>と基質<math>S</math>が互いに異なる部位に独立に結合し、互いの結合に影響を及ぼさないような場合、これを非競合阻害(非拮抗阻害:noncompetitive inhibition)と呼ぶ。この場合、(1)(19)の反応スキームに加えて
<br> <math>ES + I {\rightleftarrows} ESI</math> (27)
<br> <math>EI + S {\rightleftarrows} ESI</math> (28)
という結合解離平衡の存在を仮定することになるが、(27)(28)の解離平衡定数は、互いの結合に影響を及ぼさないという定義により、それぞれ<math>K_i</math>, <math>K_d</math>と等しくなる。すなわち、
<br> <math>K_i = \frac{[E][I]}{[EI]} = \frac{[ES][I]}{[ESI]}</math> (29)
<br> <math>K_d = \frac{[E][S]}{[ES]} = \frac{[EI][S]}{[ESI]}</math> (30)
また酵素の全濃度<math>[E]_0</math>は
<br> <math>[E]_0 = [E] + [ES] + [EI] + [ESI]</math> (31)
となる。上記と同様に(29)(30)(31)より<math>[E]</math>、<math>[EI]</math>、<math>[ESI]</math>を消去し、得られた<math>[ES]</math>を(3)に代入して、<math>k_3[E]_0 = V_{max}</math>、<math>K_d=K_m</math>とおくと、
<br> <math>v = \frac{1}{1+\frac{[I]}{K_i}}\frac{V_{max}[S]}{K_m +[S]}</math> (32)
この式を元のミカエリス・メンテンの式 (7)式と比較すると、非競合阻害剤<math>I</math>の存在下では<math>K_m</math>は変化しないが<math>V_{max}</math>が<math>1 / (1 + [I] / K_i)</math>だけ減少していることが分かる。また、(14)や(24)と同様に(32)式の逆数をとって整理すると
<br> <math>\frac{1}{v} = \frac{K_m(1+\frac{[I]}{K_i})}{V_{max}}\frac{1}{[S]} + \frac{1+\frac{[I]}{K_i}}{V_{max}}</math> (33)
従って<math>1 / [S]</math>に対して<math>1 / v</math>をプロットすると'''図5'''のような直線プロットとなり、様々な濃度の阻害剤<math>I</math>の存在下で実験すると、<math>x</math>軸上の一点(<math>x</math>切片<math>={-1/K_m}</math>)で交わる直線群が得られる。これらの直線の傾きは (26)式で表せるので、競合阻害の場合と同様、各阻害剤濃度<math>[I]</math>に対して、'''図5'''のラインウィーバー・バークプロットの傾きをプロットした2次プロットは'''図4'''のようになり、その直線の<math>x</math>切片の値から<math>K_i</math>値を求めることが出来る。この場合も阻害定数<math>K_i</math>は値が小さいほど酵素に対する親和性が強いことを示す。 [[Image:Atsuhikoishida fig 5.jpg|thumb|300px|'''図5.非競合阻害剤存在下のラインウィーバー・バークプロット'''<br>各直線はx軸上の一点で交わる。]]
<math>v = \frac{k_{cat}} {K_m}[E][S] </math> (18 )
以上のように、阻害剤濃度や基質濃度を様々に変えて酵素活性を測定し、'''図3'''や'''図5'''のようなラインウィーバー・バークプロットのパターンを調べることにより、その阻害剤と酵素の親和性や阻害剤の結合部位に関する情報を簡便に得ることが出来る。
この式はEとSの衝突が反応全体の速度を支配していると考えた場合の二次反応速度定数が<span class="texhtml"> ''k ''<sub> ''cat ''</sub> / ''K ''<sub>''m''</sub></span>であることを示している。<span class="texhtml">''k''<sub>''cat''</sub> / ''K''<sub>''m''</sub></span>の値は、異なる酵素の触媒効率を比較する際のパラメータとして用いられる。また、同一の酵素に対して、異なる基質の特異性を議論する場合にも<span class="texhtml">''k''<sub>''cat''</sub> / ''K''<sub>''m''</sub></span>の値が用いられ、特異性定数と呼ばれることがある。この場合、<span class="texhtml">''k''<sub>''cat''</sub> / ''K''<sub>''m''</sub></span>の値が大きいほど、その酵素に対してよい基質であるということになる。このように(7)式または(13)式から得られる各種の速度論的パラメータは、酵素の反応特異性や反応機構に関して、しばしば重要な知見を与える<ref><pubmed>1646810</pubmed></ref>,<ref><pubmed>11328597</pubmed></ref>。
== 酵素反応速度論的解析の実例 ==
== 関連項目 ==
以上述べてきたような各種の速度論的パラメータは、酵素の反応特異性や反応機構に関して、しばしば重要な知見を与える。神経科学分野で重要な役割を担ういくつかの酵素においてもこのような解析がなされている。例えば[[カテコールアミン]]の生合成に重要な役割を果たす[[カテコールアミン#合成|チロシン水酸化酵素]]では、[[cAMP依存性タンパク質リン酸化酵素]] (Aキナーゼ)<ref><pubmed>6102382</pubmed></ref>や[[Ca2+/リン脂質依存性タンパク質リン酸化酵素|Ca<sup>2+</sup>/リン脂質依存性タンパク質リン酸化酵素]] (Cキナーゼ)<ref><pubmed>6151178</pubmed></ref>によってリン酸化されると、[[wj:補酵素|補酵素]]アナログである6-メチルテトラヒドロビオプテリンに対する<math>K_m</math>が著明に減少し、補酵素との親和性が高まって活性化されることが示されている。
* [[酵素反応速度論 ]]
* [[速度論的パラメータ ]]
* [[K_m(ミカエリス定数)| <math >K_m </math >(ミカエリス定数)]]
* [[V_max |<math >V_{max} </math >]]
* [[k_cat(触媒定数) |<math>k_{cat} </math>(触媒定数)]]
*[[酵素基質複合体(ES complex、ミカエリス複合体)]]
*[[酵素活性]]
*[[ラインウィーバー・バークプロット]]
*[[基質特異性]]
[[記憶学習]]に深く関係することが明らかとなっているCaMキナーゼⅡに関しても、詳細な速度論的解析がなされている。CaMキナーゼⅡはThr286が自己リン酸化されるとCa<sup>2+</sup>/CaM ([[カルモジュリン]])に非依存的な活性が出現し、この活性が記憶やその素過程と考えられる[[長期増強現象]]の成立に重要な役割を果たすと考えられているが、様々な基質を用いて速度論的解析を行った結果、このCa<sup>2+</sup>/CaM非依存性活性ではCa<sup>2+</sup>/CaM存在下の活性に比べて、<math>V_{max}</math>には変化がないものの、調べた全ての基質に関して<math>K_m</math>が増大しており、基質との親和性が低下していることが判明した<ref><pubmed>1646810</pubmed></ref>。また、本酵素の活性制御に重要な役割を果たす自己阻害ドメインの合成ペプチドを用いて'''図3'''や'''図5'''のような阻害実験を行うことにより、活性制御機構に関する重要な知見が得られている<ref><pubmed>2538462</pubmed></ref>。同様に自己リン酸化部位Thr286周辺の配列を模した合成阻害ペプチドを用いて阻害実験を行うことにより、少なくとも2種類の異なる基質結合部位が存在することが初めて示唆されたが<ref><pubmed>7836445</pubmed></ref>、この結果は、後に本酵素の活性制御機構や[[NMDA型グルタミン酸受容体]]との相互作用を解明する上で不可欠となるT-site、S-siteという2種類の基質結合部位に関する概念<ref><pubmed>11459059</pubmed></ref>を確立する上で、先駆的な役割を果たしている。
== 参考文献 ==
== 関連項目 ==
<references/>
*[[酵素反応速度論]]
*[[速度論的パラメータ]]
*[[ミカエリス定数]]
*[[Vmax]]
*[[触媒定数]]
*[[酵素基質複合体]] ([[ミカエリス複合体]])
*[[酵素活性]]
*[[阻害剤]]
*[[基質特異性]]
== 参考文献 ==
<references />
(執筆者:石田敦彦 担当編集委員:林康紀)
英語名:Michaelis-Menten plot
同義語: S-vプロット、ミカエリス・メンテンの式、ブリッグス・ホールデンの式
ミカエリス・メンテンの式 L. Michaelis とM. L. Menten はインベルターゼ に関する研究において、酵素 の反応速度と基質 濃度の関係を明らかにするため、酵素と基質が結合した酵素基質複合体(ES complex)を形成することにより酵素反応 が進行するとの概念に基づいて、次のような反応スキームを考えた。
E
+
S
⇄
k
2
k
1
E
S
→
k
3
E
+
P
{\displaystyle E+S{\overset {k_{1}}{\underset {k_{2}}{\rightleftarrows }}}ES{\xrightarrow {k_{3}}}E+P}
ここに
E
{\displaystyle E}
S
{\displaystyle S}
P
{\displaystyle P}
K
1
{\displaystyle K_{1}}
K
2
{\displaystyle K_{2}}
K
3
{\displaystyle K_{3}}
E
S
{\displaystyle ES}
E
{\displaystyle E}
S
{\displaystyle S}
平衡状態 にあって、
K
3
{\displaystyle K_{3}}
速度定数 とする過程が全体の酵素反応の律速段階 であると仮定すれば、ES complexの解離平衡定数
K
d
{\displaystyle K_{d}}
K
d
=
[
E
]
[
S
]
[
E
S
]
=
k
2
k
1
{\displaystyle K_{d}={\frac {[E][S]}{[ES]}}={\frac {k_{2}}{k_{1}}}}
v
{\displaystyle v}
v
=
k
3
[
E
S
]
{\displaystyle v=k_{3}[ES]\,}
[
E
0
]
{\displaystyle [E_{0}]}
[
E
0
]
=
[
E
]
+
[
E
S
]
{\displaystyle [E_{0}]=[E]+[ES]\,}
[
E
]
{\displaystyle [E]}
[
E
S
]
=
[
E
0
]
[
S
]
K
d
+
[
S
]
{\displaystyle [ES]={\frac {[E_{0}][S]}{K_{d}+[S]}}}
v
=
k
3
[
E
S
]
=
k
3
[
E
0
]
[
S
]
K
d
+
[
S
]
{\displaystyle v=k_{3}[ES]={\frac {k_{3}[E_{0}][S]}{K_{d}+[S]}}}
v
=
k
3
[
E
0
]
=
V
m
a
x
{\displaystyle v=k_{3}[E_{0}]=V_{max}}
k
d
=
k
m
{\displaystyle k_{d}=k_{m}}
v
=
k
3
[
E
S
]
=
V
m
a
x
[
S
]
K
m
+
[
S
]
{\displaystyle v=k_{3}[ES]={\frac {V_{max}[S]}{K_{m}+[S]}}}
この(7)式をミカエリス・メンテンの式と呼び、1913年にドイツの学術雑誌に発表された[ 1] [ 2]
K
m
{\displaystyle K_{m}}
V
m
a
x
{\displaystyle V_{max}}
K
m
{\displaystyle K_{m}}
K
d
{\displaystyle K_{d}}
ブリッグス・ホールデンの式 しかしながら、上記、Michaelis とMentenの考えではいくつかの仮定を設けており、常にこれらの仮定が成立するとは限らない。そこで1925年にG. E. Briggs とJ. B. S. Haldane は、ミカエリス・メンテンの式の、より一般化された誘導法を示した[ 3]
[
E
S
]
{\displaystyle [ES]}
d
[
E
S
]
d
t
=
0
=
k
1
[
E
]
[
S
]
−
k
2
[
E
S
]
−
k
3
[
E
S
]
{\displaystyle {\frac {d[ES]}{dt}}=0=k_{1}[E][S]-k_{2}[ES]-k_{3}[ES]}
[
E
0
]
{\displaystyle [E_{0}]}
[
E
0
]
=
[
E
]
+
[
E
S
]
{\displaystyle [E_{0}]=[E]+[ES]\,}
[E ] を消去すると
[
E
S
]
=
k
1
[
E
0
]
[
S
]
k
1
[
S
]
+
(
k
2
+
k
3
)
{\displaystyle [ES]={\frac {k_{1}[E_{0}][S]}{k_{1}[S]+(k_{2}+k_{3})}}}
v
v
=
k
3
[
E
S
]
{\displaystyle v=k_{3}[ES]\,}
v
=
k
1
k
3
[
E
0
]
[
S
]
k
1
[
S
]
+
(
k
2
+
k
3
)
=
k
3
[
E
0
]
[
S
]
[
S
]
+
k
2
+
k
3
k
1
{\displaystyle v={\frac {k_{1}k_{3}[E_{0}][S]}{k_{1}[S]+(k_{2}+k_{3})}}={\frac {k_{3}[E_{0}][S]}{[S]+{\frac {k_{2}+k_{3}}{k_{1}}}}}}
(
k
2
+
k
3
)
/
k
1
=
K
m
{\displaystyle (k_{2}+k_{3})/k_{1}=K_{m}}
k
3
[
E
0
]
=
V
m
a
x
{\displaystyle k_{3}[E_{0}]=V_{max}}
v
=
k
3
[
E
S
]
=
V
m
a
x
[
S
]
K
m
+
[
S
]
{\displaystyle v=k_{3}[ES]={\frac {V_{max}[S]}{K_{m}+[S]}}}
K
m
{\displaystyle K_{m}}
K
d
{\displaystyle K_{d}}
K
2
>>
K
3
{\displaystyle K_{2}>>K_{3}}
K
m
{\displaystyle K_{m}}
k
2
{\displaystyle k_{2}}
k
1
{\displaystyle k_{1}}
K
d
{\displaystyle K_{d}}
K m
K
m
{\displaystyle K_{m}}
V
m
a
x
{\displaystyle V_{m}ax}
ミカエリス・メンテンプロット 図.基質濃度と酵素活性の関係 (ミカエリス・メンテンプロット、またはS-vプロット) (7)式も(13)式も、酵素反応速度(すなわち酵素活性)と基質濃度の関係を定量的に表した式である。実験的には様々な基質濃度で酵素活性を測定し、横軸に基質濃度、縦軸に酵素活性をとってプロットした場合、図に示すように、数学的には直角双曲線 の形となる。このようなプロットをミカエリス・メンテンプロット(S-vプロット)と呼ぶ。図から明らかなように、基質濃度がK m V max K m V max K m
速度論的パラメータの求め方 図1のようなミカエリス・メンテンプロットより、上記K m V max
1
v
=
K
m
V
m
a
x
1
[
S
]
+
1
V
m
a
x
{\displaystyle {\frac {1}{v}}={\frac {K_{m}}{V_{max}}}{\frac {1}{[S]}}+{\frac {1}{V_{max}}}}
とし、1/[S]に対して1/vをプロットして得られる直線プロット(ラインウィーバー・バークプロット )のx切片及びy切片より
K
m
{\displaystyle K_{m}}
V
m
a
x
{\displaystyle V_{max}}
(7)式または(13)式(ミカエリス・メンテンの式またはブリッグス・ホールデンの式)は多くの酵素にあてはまる便利な式であるが、(1)の反応スキームに従うことを前提にしているので、当然これにあてはまらない場合も存在する。そのような場合に(7)式または(13)式を無理にあてはめて解析することは、誤った結論を導く可能性があるので注意が必要である。そのような場合の扱いに関しては、例えば以下の文献を参照されたい[ 4]
速度論的パラメータの意味 前にも述べたように、K m V max V max V max k 3 [E 0 ]k 3 触媒定数 、或いはターンオーバー・ナンバーと呼び、通常k cat
k
c
a
t
=
V
m
a
x
[
E
0
]
{\displaystyle k_{cat}={\frac {V_{max}}{[E_{0}]}}}
である([E 0 ] は全酵素濃度)。k cat s − 1 k cat V max k cat E 0 ]
v
=
k
3
[
E
S
]
=
k
c
a
t
[
E
0
]
[
S
]
K
m
+
[
S
]
{\displaystyle v=k_{3}[ES]={\frac {k_{cat}[E_{0}][S]}{K_{m}+[S]}}}
ここで基質濃度が非常に希薄な[S ] < < K m の濃度領域を考えると
v
=
k
c
a
t
[
E
0
]
[
S
]
K
m
+
[
S
]
≈
k
c
a
t
[
E
0
]
[
S
]
K
m
=
k
c
a
t
K
m
[
E
0
]
[
S
]
{\displaystyle v={\frac {k_{cat}[E_{0}][S]}{K_{m}+[S]}}\approx {\frac {k_{cat}[E_{0}][S]}{K_{m}}}={\frac {k_{cat}}{K_{m}}}[E_{0}][S]}
基質が非常に薄い条件下では、基質は殆ど酵素に結合していないと考えられるから
[
E
0
]
≈
[
E
]
{\displaystyle [E_{0}]\approx [E]}
従って
v
=
k
c
a
t
K
m
[
E
]
[
S
]
{\displaystyle v={\frac {k_{cat}}{K_{m}}}[E][S]}
この式はEとSの衝突が反応全体の速度を支配していると考えた場合の二次反応速度定数がk cat K m k cat K m k cat K m k cat K m [ 5] [ 6]
関連項目 参考文献
↑
Michaelis, L., Menten, M.L., Johnson, K.A., & Goody, R.S. (2011). Biochemistry , 50(39), 8264-9.
[PubMed:21888353 ]
[PMC ]
[WorldCat ]
[DOI ]
↑ 鈴木紘一、笠井献一、宗川吉汪 監訳東京化学同人 (東京) :2008 ↑
Briggs, G.E., & Haldane, J.B. (1925). The Biochemical journal , 19(2), 338-9.
[PubMed:16743508 ]
[PMC ]
[WorldCat ]
[DOI ]
↑ 堀尾武一、山下仁平南江堂 (東京) :1981 ↑
Ikeda, A., Okuno, S., & Fujisawa, H. (1991). The Journal of biological chemistry , 266(18), 11582-8.
[PubMed:1646810 ]
[WorldCat ]
↑
Ishida, A., Shigeri, Y., Tatsu, Y., Endo, Y., Kameshita, I., Okuno, S., ..., & Fujisawa, H. (2001). Journal of biochemistry , 129(5), 745-53.
[PubMed:11328597 ]
[WorldCat ]
[DOI ]









![{\displaystyle K_{d}={\frac {[E][S]}{[ES]}}={\frac {k_{2}}{k_{1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d8d8b8bb255d6f7a9055904d2663dda5f1cc03c)

![{\displaystyle v=k_{3}[ES]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/470759c2df3dffd24de90535c86cbf0dd33523e6)
![{\displaystyle [E_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09236a165b89deb1ca4a526d27507640018c0bf8)
![{\displaystyle [E_{0}]=[E]+[ES]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4472f0c3b9cc7fb11de0e1928582ff1399995d8)
![{\displaystyle [E]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a170d18691c57fbfee5802ee401bd9f84ac8804b)
![{\displaystyle [ES]={\frac {[E_{0}][S]}{K_{d}+[S]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10c46040ce2c698072965fa482e386ff6cc14e4c)
![{\displaystyle v=k_{3}[ES]={\frac {k_{3}[E_{0}][S]}{K_{d}+[S]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71941aacda4fcaa7289a38338a2eb868ecab95dd)
![{\displaystyle v=k_{3}[E_{0}]=V_{max}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/254b185a907ff028c9ed2fbc23afc6301a54be7b)

![{\displaystyle v=k_{3}[ES]={\frac {V_{max}[S]}{K_{m}+[S]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea0a12c43b721dbdc43f2f9809852669700b865b)


![{\displaystyle [ES]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31639ab6b9c7c728139b5f8ce03991d800ac7741)
![{\displaystyle {\frac {d[ES]}{dt}}=0=k_{1}[E][S]-k_{2}[ES]-k_{3}[ES]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/173dd9b63c2d5d73be56e3551c85551ea710c086)
![{\displaystyle [ES]={\frac {k_{1}[E_{0}][S]}{k_{1}[S]+(k_{2}+k_{3})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80e18836e284675af4355e804f36f0063e9a3e38)
![{\displaystyle v={\frac {k_{1}k_{3}[E_{0}][S]}{k_{1}[S]+(k_{2}+k_{3})}}={\frac {k_{3}[E_{0}][S]}{[S]+{\frac {k_{2}+k_{3}}{k_{1}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d788fd0d7b1fabccebdb6165429540da26faf812)

![{\displaystyle k_{3}[E_{0}]=V_{max}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/004fbb7d372ca3c43befa51ceefdef2e8124f079)




![{\displaystyle {\frac {1}{v}}={\frac {K_{m}}{V_{max}}}{\frac {1}{[S]}}+{\frac {1}{V_{max}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e01b24fd3322236f17dabe08f4392bc4374f2a5b)
![{\displaystyle k_{cat}={\frac {V_{max}}{[E_{0}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e301ceb37495b61b840ff15980200ad4c80785c5)
![{\displaystyle v=k_{3}[ES]={\frac {k_{cat}[E_{0}][S]}{K_{m}+[S]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5df3c53399d91bbf92ce17b8bdeeecc6c793ce7)
![{\displaystyle v={\frac {k_{cat}[E_{0}][S]}{K_{m}+[S]}}\approx {\frac {k_{cat}[E_{0}][S]}{K_{m}}}={\frac {k_{cat}}{K_{m}}}[E_{0}][S]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5894644eea717d60f02a131086387def6be05290)
![{\displaystyle [E_{0}]\approx [E]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/284286ee5355dba3058b086fc87a1c07906fccf5)
![{\displaystyle v={\frac {k_{cat}}{K_{m}}}[E][S]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07bb6087713ffefcf5d71c2ade0031561aa3d135)
