「カルシウムドメイン」の版間の差分
細 →サイズ |
細編集の要約なし |
||
| (2人の利用者による、間の5版が非表示) | |||
| 12行目: | 12行目: | ||
== カルシウムドメイン仮説 == | == カルシウムドメイン仮説 == | ||
[[Image:Calciumdomain-1.png|thumb|350px|'''図.カルシウムドメイン'''<br>[[カルシウム]]イオンがチャネルを通過して生じる細胞内の遊離カルシウム濃度上昇の空間的分布領域。細胞質にある内在性カルシウムバッファーの作用により、細胞膜の内側に沿って半円形に濃度分布すると推定される。ここでは既知のキレート剤によって濃度が起点濃度の1/e (37%)となる距離を示す。]] | [[Image:Calciumdomain-1.png|thumb|350px|'''図.カルシウムドメイン'''<br>[[カルシウム]]イオンがチャネルを通過して生じる細胞内の遊離カルシウム濃度上昇の空間的分布領域。細胞質にある内在性カルシウムバッファーの作用により、細胞膜の内側に沿って半円形に濃度分布すると推定される。ここでは既知のキレート剤によって濃度が起点濃度の1/e(37%)となる距離を示す。]] | ||
Chad & Eckert<ref name="ref1"><pubmed>6329349</pubmed></ref>によって提唱された。[[電位依存性カルシウムチャネル]]が短時間、開口することにより、細胞外から細胞内に流入したカルシウムは、[[細胞質]]にある内在性[[カルシウムバッファー]]の影響下、拡散により、[[細胞膜]]の内側に沿って半円形に濃度分布すると推定され、その空間分布をカルシウムドメインと呼んだ(図)。カルシウムドメインを形成する最小ユニットは単一チャネルであるが、複数チャネルがクラスターを形成すると、より大きなカルシウムドメインが形成される。カルシウムドメインの重複の程度はチャネル当たりのカルシウム流入量、カルシウムチャネルの分布密度、カルシウムバッファーの濃度と結合速度などによって決定される。 | Chad & Eckert<ref name="ref1"><pubmed>6329349</pubmed></ref>によって提唱された。[[電位依存性カルシウムチャネル]]が短時間、開口することにより、細胞外から細胞内に流入したカルシウムは、[[細胞質]]にある内在性[[カルシウムバッファー]]の影響下、拡散により、[[細胞膜]]の内側に沿って半円形に濃度分布すると推定され、その空間分布をカルシウムドメインと呼んだ(図)。カルシウムドメインを形成する最小ユニットは単一チャネルであるが、複数チャネルがクラスターを形成すると、より大きなカルシウムドメインが形成される。カルシウムドメインの重複の程度はチャネル当たりのカルシウム流入量、カルシウムチャネルの分布密度、カルシウムバッファーの濃度と結合速度などによって決定される。 | ||
| 19行目: | 19行目: | ||
#細胞外カルシウムの細胞内流入を媒介するチャネル:電位依存性カルシウムチャネル、カルシウム透過型チャネル([[NMDA型グルタミン酸受容体]]チャネル、[[機械力受容チャネル]]、[[TRPチャネル]]、[[環状ヌクレオチド依存性チャネル]]、[[store-operated CRAC]]チャネルなど)<br> | #細胞外カルシウムの細胞内流入を媒介するチャネル:電位依存性カルシウムチャネル、カルシウム透過型チャネル([[NMDA型グルタミン酸受容体]]チャネル、[[機械力受容チャネル]]、[[TRPチャネル]]、[[環状ヌクレオチド依存性チャネル]]、[[store-operated CRAC]]チャネルなど)<br> | ||
#[[細胞内カルシウムストア]]から細胞質への流出を媒介するチャネル:[[リアノジン受容体]]チャネル、[[IP3受容体 | #[[細胞内カルシウムストア]]から細胞質への流出を媒介するチャネル:[[リアノジン受容体]]チャネル、[[IP3受容体]]チャネル。 | ||
==機能的役割 == | ==機能的役割 == | ||
#カルシウムチャネルの調節:細部内カルシウムによってカルシウムチャネルは活性化または不活性化される。 | #カルシウムチャネルの調節:細部内カルシウムによってカルシウムチャネルは活性化または不活性化される。 | ||
# | #カルシウム依存性チャネルの活性化:カルシウム依存性[[カリウムチャネル]]、カルシウム依存性クロライドチャネルが知られる。 | ||
#[[神経伝達物質]]の[[開口放出]]:[[シナプトタグミン]]などの低親和性カルシウム結合タンパク質により媒介される。 | #[[神経伝達物質]]の[[開口放出]]:[[シナプトタグミン]]などの低親和性カルシウム結合タンパク質により媒介される。 | ||
#[[シナプス小胞]]の取り込み([[エンドサイトーシス]]):シナプトタグミンなどの低親和性カルシウム結合タンパク質により媒介されるものと、[[カルモジュリン]] | #[[シナプス小胞]]の取り込み([[エンドサイトーシス]]):シナプトタグミンなどの低親和性カルシウム結合タンパク質により媒介されるものと、[[カルモジュリン]]などの比較的低親和性カルシウム結合タンパク質により媒介されるものがあると推定されている<ref><pubmed>20562869</pubmed></ref>。 | ||
#[[シナプス伝達]] | #[[シナプス伝達]]の修飾:カルモジュリンとの結合を介して、後シナプス受容体の密度を調節し、また前シナプス末端からの伝達物質放出を増強する。 | ||
#[[筋収縮]]。 | #[[筋収縮]]。 | ||
# | #細胞内ストアカルシウムの放出促進(リアノジン受容体チャネル、IP3受容体チャネルからのカルシウムに依存したカルシウムの放出)。 | ||
#[[成長円錐]]の伸長( | #[[成長円錐]]の伸長(TRPCチャネルなどからのカルシウム流入)。 | ||
==サイズ == | ==サイズ == | ||
カルシウムドメインのサイズは、多くの場合、光学解像度の限界を超えるため実測できない。そのため次善の策として、カルシウム結合速度の異なる[[カルシウムキレート剤]] | カルシウムドメインのサイズは、多くの場合、光学解像度の限界を超えるため実測できない。そのため次善の策として、カルシウム結合速度の異なる[[カルシウムキレート剤]](表)を細胞内に負荷して、それによるカルシウム依存性機能の抑制率を定量して、ドメインサイズを推定することが行われている。 | ||
{|class="wikitable" | {|class="wikitable" | ||
| 48行目: | 48行目: | ||
|- | |- | ||
| [[EGTA]]<ref name=ref11106608 /> | | [[EGTA]]<ref name=ref11106608 /> | ||
| 1.0 x 10<sup> | | 1.0 x 10<sup>6</sup> | ||
| 0.07 | | 0.07 | ||
|} | |} | ||
| 56行目: | 56行目: | ||
λ = (D<sub>Ca</sub>/K<sub>on</sub>B)<sup>0.5</sup> | λ = (D<sub>Ca</sub>/K<sub>on</sub>B)<sup>0.5</sup> | ||
で与えられる。ここでD<sub>Ca</sub>は細胞質内におけるカルシウムの[[wikipedia:ja:拡散定数|拡散定数]](220 | で与えられる。ここでD<sub>Ca</sub>は細胞質内におけるカルシウムの[[wikipedia:ja:拡散定数|拡散定数]](220 μm2/s)<ref name="ref2"><pubmed>9278532</pubmed></ref>、Bはキレート剤の濃度に相当する。この式から算定されるカルシウムドメインのλは図1のようになる。 例えば、細胞内に1 mM EGTAが存在すると起点から105 nm離れた位置におけるカルシウム濃度は起点濃度の1/e(37%)となる。同様に、細胞内に1 mM BAPTAが存在する場合のカルシウム拡散の長さ定数は23 nmと算定される(図1b)。したがって、一定濃度のEGTAまたはBAPTAを細胞内に注入し、それによるカルシウム依存性機能の抑制率を測定することによって、この機能に関わるカルシウムドメインのサイズを推定することができる。 | ||
==マイクロドメインとナノドメイン == | ==マイクロドメインとナノドメイン == | ||
便宜上、カルシウムドメインのサイズが10-20 | 便宜上、カルシウムドメインのサイズが10-20 nm以下のものをナノドメイン、100-200 nm以上のものをマイクロドメインと呼び分けることが行われている<ref name="ref3"><pubmed>9539117</pubmed></ref>。例えば、「ナノドメインカルシウムに依存する小胞開口放出」のように使われている。しかし一方「マイクロドメイン」はカルシウムドメインの総称としても使われているので注意を要する。 | ||
==関連項目== | ==関連項目== | ||
2014年10月7日 (火) 13:36時点における版
高橋 智幸
同志社大学 生命医科学部医生命システム学科
DOI:10.14931/bsd.2643 原稿受付日:2012年10月18日 原稿完成日:2014年10月7日
担当編集委員:林 康紀(独立行政法人理化学研究所)
英語名:Calcium domain
カルシウムイオン(Ca2+)がチャネルを通過して生じる細胞内の遊離カルシウム濃度上昇の空間的分布領域。カルシウムドメインは細胞外からのカルシウム流入、または小胞体からのカルシウム流出によって形成される。
カルシウムドメイン仮説
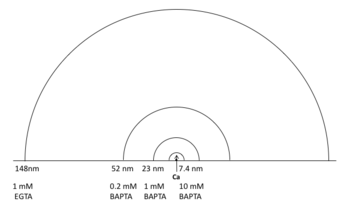
カルシウムイオンがチャネルを通過して生じる細胞内の遊離カルシウム濃度上昇の空間的分布領域。細胞質にある内在性カルシウムバッファーの作用により、細胞膜の内側に沿って半円形に濃度分布すると推定される。ここでは既知のキレート剤によって濃度が起点濃度の1/e(37%)となる距離を示す。
Chad & Eckert[1]によって提唱された。電位依存性カルシウムチャネルが短時間、開口することにより、細胞外から細胞内に流入したカルシウムは、細胞質にある内在性カルシウムバッファーの影響下、拡散により、細胞膜の内側に沿って半円形に濃度分布すると推定され、その空間分布をカルシウムドメインと呼んだ(図)。カルシウムドメインを形成する最小ユニットは単一チャネルであるが、複数チャネルがクラスターを形成すると、より大きなカルシウムドメインが形成される。カルシウムドメインの重複の程度はチャネル当たりのカルシウム流入量、カルシウムチャネルの分布密度、カルシウムバッファーの濃度と結合速度などによって決定される。
関与するチャネル
- 細胞外カルシウムの細胞内流入を媒介するチャネル:電位依存性カルシウムチャネル、カルシウム透過型チャネル(NMDA型グルタミン酸受容体チャネル、機械力受容チャネル、TRPチャネル、環状ヌクレオチド依存性チャネル、store-operated CRACチャネルなど)
- 細胞内カルシウムストアから細胞質への流出を媒介するチャネル:リアノジン受容体チャネル、IP3受容体チャネル。
機能的役割
- カルシウムチャネルの調節:細部内カルシウムによってカルシウムチャネルは活性化または不活性化される。
- カルシウム依存性チャネルの活性化:カルシウム依存性カリウムチャネル、カルシウム依存性クロライドチャネルが知られる。
- 神経伝達物質の開口放出:シナプトタグミンなどの低親和性カルシウム結合タンパク質により媒介される。
- シナプス小胞の取り込み(エンドサイトーシス):シナプトタグミンなどの低親和性カルシウム結合タンパク質により媒介されるものと、カルモジュリンなどの比較的低親和性カルシウム結合タンパク質により媒介されるものがあると推定されている[2]。
- シナプス伝達の修飾:カルモジュリンとの結合を介して、後シナプス受容体の密度を調節し、また前シナプス末端からの伝達物質放出を増強する。
- 筋収縮。
- 細胞内ストアカルシウムの放出促進(リアノジン受容体チャネル、IP3受容体チャネルからのカルシウムに依存したカルシウムの放出)。
- 成長円錐の伸長(TRPCチャネルなどからのカルシウム流入)。
サイズ
カルシウムドメインのサイズは、多くの場合、光学解像度の限界を超えるため実測できない。そのため次善の策として、カルシウム結合速度の異なるカルシウムキレート剤(表)を細胞内に負荷して、それによるカルシウム依存性機能の抑制率を定量して、ドメインサイズを推定することが行われている。
| キレート剤 | 結合速度定数(Kon)(1/M・s) | 解離定数(KD) (μM) |
| BAPTA[3] | 4.0 x 108 | 0.22 |
| EGTA[4] | 1.0 x 106 | 0.07 |
キレート剤の存在下におけるカルシウムの拡散距離長さ定数λは
λ = (DCa/KonB)0.5
で与えられる。ここでDCaは細胞質内におけるカルシウムの拡散定数(220 μm2/s)[3]、Bはキレート剤の濃度に相当する。この式から算定されるカルシウムドメインのλは図1のようになる。 例えば、細胞内に1 mM EGTAが存在すると起点から105 nm離れた位置におけるカルシウム濃度は起点濃度の1/e(37%)となる。同様に、細胞内に1 mM BAPTAが存在する場合のカルシウム拡散の長さ定数は23 nmと算定される(図1b)。したがって、一定濃度のEGTAまたはBAPTAを細胞内に注入し、それによるカルシウム依存性機能の抑制率を測定することによって、この機能に関わるカルシウムドメインのサイズを推定することができる。
マイクロドメインとナノドメイン
便宜上、カルシウムドメインのサイズが10-20 nm以下のものをナノドメイン、100-200 nm以上のものをマイクロドメインと呼び分けることが行われている[5]。例えば、「ナノドメインカルシウムに依存する小胞開口放出」のように使われている。しかし一方「マイクロドメイン」はカルシウムドメインの総称としても使われているので注意を要する。
関連項目
参考文献
- ↑
Chad, J.E., & Eckert, R. (1984).
Calcium domains associated with individual channels can account for anomalous voltage relations of CA-dependent responses. Biophysical journal, 45(5), 993-9. [PubMed:6329349] [PMC] [WorldCat] [DOI] - ↑
Yamashita, T., Eguchi, K., Saitoh, N., von Gersdorff, H., & Takahashi, T. (2010).
Developmental shift to a mechanism of synaptic vesicle endocytosis requiring nanodomain Ca2+. Nature neuroscience, 13(7), 838-44. [PubMed:20562869] [PMC] [WorldCat] [DOI] - ↑ 3.0 3.1 3.2
Naraghi, M., & Neher, E. (1997).
Linearized buffered Ca2+ diffusion in microdomains and its implications for calculation of [Ca2+] at the mouth of a calcium channel. The Journal of neuroscience : the official journal of the Society for Neuroscience, 17(18), 6961-73. [PubMed:9278532] [WorldCat] - ↑ 4.0 4.1
Nägerl, U.V., Novo, D., Mody, I., & Vergara, J.L. (2000).
Binding kinetics of calbindin-D(28k) determined by flash photolysis of caged Ca(2+) Biophysical journal, 79(6), 3009-18. [PubMed:11106608] [PMC] [WorldCat] [DOI] - ↑
Neher, E. (1998).
Vesicle pools and Ca2+ microdomains: new tools for understanding their roles in neurotransmitter release. Neuron, 20(3), 389-99. [PubMed:9539117] [WorldCat] [DOI]