「神経符号化」の版間の差分
| (2人の利用者による、間の12版が非表示) | |||
| 1行目: | 1行目: | ||
北海道大学人間知・脳・AI研究教育センター | |||
神経符号化 | |||
<div align="right"> | <div align="right"> | ||
<font size="+1">[http://researchmap.jp/shimazaki | <font size="+1">[http://researchmap.jp/shimazaki 島崎秀昭]</font><br> | ||
''北海道大学人間知・脳・AI研究教育センター''<br> | ''北海道大学人間知・脳・AI研究教育センター''<br> | ||
DOI:<selfdoi /> | DOI:<selfdoi /> 原稿受付日:2021年8月3日 原稿完成日:2021年8月X日<br> | ||
担当編集委員:[https://researchmap.jp/kkitajo 北城 圭一](生理学研究所)<br> | 担当編集委員:[https://researchmap.jp/kkitajo 北城 圭一](生理学研究所)<br> | ||
</div> | </div> | ||
同義語:神経コード<br> | 同義語:神経コード<br> | ||
英:neural | 英:neural coding | ||
{{box|text= 神経符号化とは、外界の刺激が神経活動に変換・表現され、行動を担う神経活動が生成される過程を指す。刺激・行動と神経活動の関係を記述し、刺激の認識や行動生成を担う神経活動とその機構を同定することで、この過程を明らかにする研究を神経符号化研究(neural coding studies)という。同定された神経活動・機構を神経符号(neural code)と呼ぶ。}} | {{box|text= 神経符号化とは、外界の刺激が神経活動に変換・表現され、行動を担う神経活動が生成される過程を指す。刺激・行動と神経活動の関係を記述し、刺激の認識や行動生成を担う神経活動とその機構を同定することで、この過程を明らかにする研究を神経符号化研究(neural coding studies)という。同定された神経活動・機構を神経符号(neural code)と呼ぶ。}} | ||
==神経符号化とその研究方法== | ==神経符号化とその研究方法== | ||
神経符号化は外界の刺激が神経活動に変換・表現され、行動を担う神経活動が生成される過程を指す。刺激の認識や行動生成を担う神経活動とそのメカニズムを同定することで、この過程を明らかにする研究を神経符号化研究という。具体的には、神経系のどの部位のどのタイプの神経細胞のどのような活動が、動物の認識・行動を説明するのに必要かつ十分であるかを明らかにすることで、外界の刺激が神経活動に変換され行動に至る過程を解明することを目指す研究領域である。Johns Hopkins大学のVernon Mountcastleは振動の感覚に関わる受容器を特定する次のような手法で、神経符号化研究の古典的な方法論を確立した<ref name=Mountcastle1972><pubmed>4621505</pubmed></ref><ref name=カンデル2014>'''日本語版監修 金澤一郎・宮下保司 (2014).'''<br>カンデル神経科学第5版 第21章感覚の符号化・第23章触覚 メディカル・サイエンス・インターナショナル社</ref> [Mountcastle 1972; カンデル神経科学2014]。 | |||
人間の手には圧力・振動・温度などの物理刺激に反応する12種類の受容器がある。特に指先には触覚に関わる4種類の機械受容器がある。表皮にあるマイスネル小体・メルケル受容器 、深皮にあるラフィニ終末・パチニ小体がそれである。これらの受容器は末梢神経細胞の軸索の終末にあり、そのもう一端は脊髄に投射する。脊髄の神経細胞から先は視床を介して体性感覚野に投射があり、我々の触知覚を担っている。4つの受容器は外界からの力の異なる特徴に対して反応し、順応特性が異なる。受容器が特定されているため、触覚に基づく我々の外界の認識がどの機械受容器を介した神経細胞の活動によって担われているかを問うことができる。 | |||
被験者(ヒトもしくはサル)に振動する物体を握らせ、振動の有無を報告させる。振動の振幅を変化させ、報告が可能な最小の振幅(閾値)を特定する。この作業を異なる振動数のもとで行うと、閾値は刺激の周波数に依存していることがわかる。次に同じ実験条件下で、機械受容器から投射する求心性繊維から電気記録を行うことで、振動に対する機械受容器の応答を記録し、神経活動が生じる振幅の閾値を調べる。すると、メルケル細胞の閾値は被験者の閾値よりもずっと高い位置にあり、被験者が振動を認識している状況でも活動をしていない状況があることがわかる。これにより、メルケル細胞の活動は振動の感覚を担う神経符号としては棄却される。一方、マイスネル小体・パチニ小体の閾値の周波数特性はそれぞれ低周波数(20-40Hz)・高周波数 (40-500Hz)での被験者のそれとほぼ一致することが示された。他の求心性繊維の活動は被験者の報告の結果を説明できないため、マイスネル小体・パチニ小体の活動が振動の感覚を担う神経符号であることが示された。 | |||
このように神経符号化研究では、観測者である動物に行動課題を課してそのパフォーマンスを計測する心理物理実験を行う。一方で同じ条件下で神経生理実験により神経活動を計測し、その活動から行動を予測する。そして両者の比較を行い動物の認識・行動を説明できる神経細胞・神経活動の候補を絞り込んでゆく。通常、前者は心理測定関数(psychometric function)、後者は神経測定関数(neurometric function)という形で記述される。図1に神経符号化研究の概略図を記した。ある神経細胞の特定の活動が動物の行動に必要な情報を担っている(神経符号の候補である)ためには、その神経活動の情報を用いて予測される最適な行動の成績が動物のそれを上回っていなければならない。そうでなければ、その神経細胞の活動は神経符号としては棄却される。なぜならば、行動に用いられた情報が神経活動として存在しているはずであり、その情報は計測した神経細胞もしくは行動予測に使用した活動特徴以外に存在しているはずだからである。 | |||
[[ファイル:Shimazaki Neural Coding Fig1.png|サムネイル|'''図1. 神経符号化研究の概略図'''<br>Johns Hopkins大学Kenneth O. Johnson氏による講義ノートより筆者が改変・加筆。]] | |||
ここで注意すべきは、神経活動から予測される最適な行動に基づく心理実験課題の成績は実際に動物が行動によって報告した結果に基づく成績と同じである必要はなく、それを上回っていても良いことである。末梢神経等の初期段階で利用可能な情報が意思決定に余すとこなく使用されるとは限らないからである。しかしながら驚くべきことに、いくつかの事例において行動の成績が感覚受容器のパフォーマンスに接近していることが示されている。例えば人間は少なくとも数個の光子があればその報告が可能であると推定されており<ref name=Hecht1942><pubmed>19873316</pubmed></ref><ref name=Barlow1956><pubmed>13346424</pubmed></ref><ref name=Rieke1998>'''Rieke, F. & Baylor, D. A. (1998)'''<br>Single-photon detection by rod cells of the retina. Reviews of Modern Physics. 70(3):1027</ref> | ここで注意すべきは、神経活動から予測される最適な行動に基づく心理実験課題の成績は実際に動物が行動によって報告した結果に基づく成績と同じである必要はなく、それを上回っていても良いことである。末梢神経等の初期段階で利用可能な情報が意思決定に余すとこなく使用されるとは限らないからである。しかしながら驚くべきことに、いくつかの事例において行動の成績が感覚受容器のパフォーマンスに接近していることが示されている。例えば人間は少なくとも数個の光子があればその報告が可能であると推定されており<ref name=Hecht1942><pubmed>19873316</pubmed></ref><ref name=Barlow1956><pubmed>13346424</pubmed></ref><ref name=Rieke1998>'''Rieke, F. & Baylor, D. A. (1998)'''<br>Single-photon detection by rod cells of the retina. Reviews of Modern Physics. 70(3):1027</ref>[Hecht 1942; Barlow 1956; Rieke 1998]、これは網膜視細胞の検出限界に近いと考えられている。これらの結果は、中枢神経系が効率的に入力情報を使用して行動を生成していることを示唆している<ref name=Barlow1972><pubmed>4377168</pubmed></ref>[Barlow 1972]。一方、過去の知見に依存しない課題では、末梢神経のパフォーマンスを行動のパフォーマンスが上回ることはない。我々の認識精度の上限は感覚デバイスの精度に制限され、それを上回ることはないからである。 | ||
もちろん、このような古典的な神経符号化研究の手法で行動を担う神経細胞を明快に特定できるのは、行動に必要な信号の通る経路が明らかだからである。これ以外の状況では、たとえ神経細胞から行動を予測できたとしても、行動がその部位の活動に依存すると断定することはできない。そのため損傷実験や電気刺激・光遺伝学による介入実験と組み合わせる事で、行動を担う神経活動を明らかにする事が試みられている。 | |||
Mountcastleらの神経符号化研究では神経活動から刺激の有無を推定する復号化の手法が用いられるが、刺激が神経活動へどのように変換されるかを表す符号化の方式を明らかにする事は神経符号化研究における主要な課題である。神経符号化は神経系における情報の変換と表現を指すともされ<ref name=Perkel1968>'''Perkel, D. H. & Bullock, T. H. (1968).'''<br>Neural coding. Neurosciences Research Program Bulletin</ref>[Perkel and Bullock 1968]、それぞれ符号化・復号化の手法を用いて情報神経細胞が担う情報を明らかにすることが試みられている。詳しくは次節の符号化・復号化の項目で述べる。近年では入力刺激から意思決定までをいわゆるend-to-endで実装した深層ニューラルネットワークが人間のパフォーマンスを上回ったことから、深層ニューラルネットワークの各層と脳の領野の活動を比較する新しいタイプの神経符号化研究も生まれている<ref name=Yamins2014><pubmed>24812127</pubmed></ref>[Yamins 2014]。 | |||
==符号化と復号化== | ==符号化と復号化== | ||
符号化と復号化は情報理論の用語で、文字・画像・音声などを送信者から通信路を介して受信者に伝達するために、送信者側で情報源・通信路に適した形に変換し、受信者側でそれを元に戻すことを指す。そのために用いられる機器あるいはアルゴリズムを符号器(エンコーダ)・復号器(デコーダ)と呼ぶ。神経科学の文脈では、符号化は刺激が神経活動に変換されることに対応し、刺激が与えられたもとで神経細胞の活動を表すモデルを符号器、神経活動が与えられたもとで刺激を表すモデルを復号器と呼ぶ。多くの場合、これらは統計モデルを用いて記述される。統計モデルによって符号器・復号器を記述することで、神経発火活動のどの特徴に情報があるかを調べる事ができる。以下に、神経符号化研究で用いられる符号化・復号化のアプローチを紹介する。 | |||
神経科学における符号化は外界の刺激を神経活動に変換する過程・機構を言う。単一神経細胞の発火頻度と刺激の関係を表す関数(チューニング関数・応答関数・活性化関数)は符号器の例であり、これらを組み合わせた人工ニューラルネットワークも符号器である。応答の確率的揺らぎも考慮すると、平均値がチューニング関数で与えられる確率分布が符号器となる。ただし、一般には平均発火頻度に限らず刺激に依存する神経活動を確率分布で表したものが符号器となる。複数の神経細胞による集団符号化の議論では、刺激に依存する神経活動の同時確率分布が符号器となる。 <math>$N$</math>個の神経細胞集団の活動を<math>$\mathbf{x}=(x_1,x_2,\ldots,x_N)$</math>で表し刺激を<math>$\mathbf{y}$</math>で表すと、同時確率分布は<math>$p(\mathbf{x}|\mathbf{y},\mathbf{w})$</math>と書くことができる。ただし、<math>$\mathbf{w}$</math>は分布のパラメータである。例えば神経活動として発火頻度を取り上げ、試行毎の実現にガウスノイズを仮定して神経活動を近似する場合には多変量正規分布が符号器となり、平均発火頻度もしくは共分散行列、あるいはその両方が刺激に依存する。神経スパイク活動に対しては刺激依存のパラメータを有する点過程モデルやイジングモデルを用いた集団活動の同時分布が符号器となる。 | |||
神経符号化研究では、神経細胞の活動のどの部分に外界の情報が表され、運ばれているのかを特定することが重要な課題になる。この課題に統計モデルを使用することのメリットは、使用するデータの特徴がモデルの十分統計量として厳密に定義される点にある。神経活動のどの特徴が外界に依存し、外界の変化とともに変わるのかについて複数の仮説が考えられる。代表的な例として、単一神経細胞の発火頻度によって刺激が符号化されるとする発火頻度符号化(rate coding)、神経スパイクの時間構造に刺激が符号化されているとする時間的符号化(temporal coding)、相関を伴う神経細胞集団の同時活動に刺激が符号化されているとする集団符号化(population coding)等が挙げられる。これらはそれぞれ符号器としてポアソン過程、非ポアソン過程、多変量ガウス分布/イジングモデル/一般化線形モデルを用いてモデル化することができ、仮説を数学的に明らかな形で取り扱うことができる。次節では、これらのうち神経符号化研究で中心的な役割を担う集団符号化について詳しく述べる。 | |||
神経細胞による符号化の実現を考えるとき、下流の神経細胞がこれらの特徴を読み取ることができるか、すなわち符号化に用いる神経活動の特徴量の変化に応じて下流の神経細胞が活動を変えることができるかを考える必要がある。個々のシナプス前細胞の発火頻度に応じてシナプス後細胞の活動が変化することは容易に実現できるため、発火頻度を神経符号の仮説として採用することが多い。しかし、樹状突起上の電位依存性チャネルによる非線形な応答を考慮すれば、シナプス入力時系列の時間構造や同期的なシナプス入力などの2次以上の統計量に依存してシナプス後細胞が活動することも容易に考えられる。そのため神経細胞によって応答が可能(符号化が可能)な特徴量を実験的・理論的に考察する事が行われてきた<ref name=Diesmann1999><pubmed>10591212</pubmed></ref><ref name=delaRocha2007><pubmed>17700699</pubmed></ref>[Diesmann 1999; De La Rocha 2007]。実際、発火頻度符号化以外の符号化方式の存在も報告されており<ref name=Ishikane2005><pubmed>15995702</pubmed></ref><ref name=Jacobs2009><pubmed>19297621</pubmed></ref>[Ishikane 2005; Jacobs 2009]、神経系は単一の符号化方式を採用するのではなく種や部位により異なる符号化方式が採用されていると考えられている。 | |||
神経符号化研究では、神経活動から刺激や行動の意図等を推定する復号器を構築・適用することで神経細胞が保持する情報を明らかにすることが行われる。復号器の構築方法には2通りの方法がある。一つ目は復号器を神経細胞の活動から直接的に作る方法である。例として、神経活動の重み付け線形和によって刺激を推定する線形モデルが挙げられる。この方法の拡張として、刺激の分布として指数分布族を用い、その期待値を連結関数を通して神経細胞活動の線形和で表す一般化線形モデルがある。これらは確率モデル<math>p(y|x,w)</math>を直接構成する方法である。二つ目の方法は、符号化で用いたモデルを使用し、符号器のパラメータ推定として刺激を推定する方法である。例えば、符号器を用いた尤度関数を使って刺激の最尤推定を行うことは復号化にあたる。この方法は刺激に対して事前分布を仮定することで、ベイズの定理を用いた事後分布による刺激の推定に一般化される。 | |||
<math> | |||
p(\mathbf{y}|\mathbf{x}, \mathbf{w})=\frac{p(\mathbf{x}|\mathbf{y}, \mathbf{w})p(\mathbf{y}|\mathbf{w})} {p(\mathbf{x}|\mathbf{w})} | p(\mathbf{y}|\mathbf{x}, \mathbf{w})=\frac{p(\mathbf{x}|\mathbf{y}, \mathbf{w})p(\mathbf{y}|\mathbf{w})} {p(\mathbf{x}|\mathbf{w})} | ||
</math> | </math> | ||
このように復号器を符号化のモデルから作成する方法を2段階法(two | このように復号器を符号化のモデルから作成する方法を2段階法(two step approach)と呼ぶ<ref name=Brown2004><pubmed>15114358</pubmed></ref>[Brown 2004]。 | ||
外界の刺激がスムーズに変化するなど、時系列になんらかの仮定をする場合、神経活動は状態空間モデルで記述される。状態空間モデルに基づく刺激の推定は、ベイズ推定を逐次的に行う逐次ベイズ推定技術を用いて解くことができる。Brownらはラットの海馬神経細胞の場所細胞の活動からラットの位置をデコードする方法として、符号器として点過程を用い、事前分布として位置が線形の状態遷移すると仮定した2段階法を用いて、海馬場所細胞のスパイク時系列からラットの位置のスムーズなデコーディングを初めて実現した<ref name=Brown2004><pubmed>15114358</pubmed></ref>[Brown 1998]。神経スパイクに対するこのような非ガウスのフィルタリング技術はブレーン・マシーン・インターフェースやブレーン・コンピュータ・インターフェースと呼ばれる神経補綴技術の基盤技術として幅広く使用されている。 | |||
ただし復号化で使用する神経活動の特徴量が複雑になってきた場合、その特徴に下流の神経細胞が反応する事は困難である事が予想される。そのため高度な神経補綴に用いられる神経活動がそのまま行動に繋がる神経符号として採用されるわけではない。また厳密には、こうして特定された神経細胞活動が行動に関わるかを調べるためには、これらの細胞を選択的に制御して行動に影響があるかを調べる必要がある。 | ただし復号化で使用する神経活動の特徴量が複雑になってきた場合、その特徴に下流の神経細胞が反応する事は困難である事が予想される。そのため高度な神経補綴に用いられる神経活動がそのまま行動に繋がる神経符号として採用されるわけではない。また厳密には、こうして特定された神経細胞活動が行動に関わるかを調べるためには、これらの細胞を選択的に制御して行動に影響があるかを調べる必要がある。 | ||
最後に、符号器にも2通りの構築方法があることを紹介する。初めに紹介したように符号器<math>p(x|y,w)</math>として神経細胞が刺激に応答するモデルを直接構築する方法のほかに、符号器をベイズの定理を用いて表す方法がある。これを用いると符号器は復号器を用いて次のように表される。 | |||
最後に、符号器にも2通りの構築方法があることを紹介する。初めに紹介したように符号器<math>p( | |||
<math> | |||
p(\mathbf{x}|\mathbf{y},\mathbf{w})=\frac{p(\mathbf{y}|\mathbf{x},\mathbf{w})p(\mathbf{x}|\mathbf{w})} {p(\mathbf{y}|\mathbf{w})} | p(\mathbf{x}|\mathbf{y},\mathbf{w})=\frac{p(\mathbf{y}|\mathbf{x},\mathbf{w})p(\mathbf{x}|\mathbf{w})} {p(\mathbf{y}|\mathbf{w})} | ||
</math> | </math> | ||
ここでパラメータ<math> | ここでパラメータ<math>$w$</math>は神経活動を生成する基盤としての脳の構造を表す。<math>p(x|w)</math>は神経活動に対する事前分布で神経活動に対する制約条件を表す。また、ここでの復号器は神経細胞活動による外界の表現/表象(representation)を記述する。事前分布と復号器を合わせた同時分布<math>p(y,x|w) =p(y|x,w)p(x|w)</math>をデータの生成モデルと呼ぶ。生成モデルはデータyが生成される過程を神経活動によって再現するモデルと見做す事ができる。従ってこの式は、刺激に対する神経細胞集団の応答活動をデータ生成のモデルによって解釈することができることを示している。 | ||
これによれば、脳の内部構造に基づく神経細胞の自発活動、すなわち脳の内発的ダイナミクスは事前分布を構成する。刺激が提示されると、神経活動は刺激の影響を受けて変調され、復号器と組み合わされて事後分布を形成する<ref name= | これによれば、脳の内部構造に基づく神経細胞の自発活動、すなわち脳の内発的ダイナミクスは事前分布を構成する。刺激が提示されると、神経活動は刺激の影響を受けて変調され、復号器と組み合わされて事後分布を形成する<ref name=Brown1998><pubmed>9736661</pubmed></ref> <ref name=Fiser2010><pubmed>20153683</pubmed></ref>[Fiser 2010; Berkes 2011]。すなわち神経応答活動は刺激を再構成・予測するための推論を行なっていると考える事ができる。神経応答活動のベイズ的な見方によれば、脳内に刺激を推定する復号器の存在を陽に仮定する必要はなくなり、復号器の役割は自発活動から刺激応答活動への変化に内包される。 | ||
生成モデルに基づく符号化研究は、正則化を課した画像の再構成という視覚野の計算論に関わる研究をその祖として古くから行われ、マルコフ確率場を用いたGeman & Gemanらによる画像再構成<ref name=Geman1984><pubmed>22499653</pubmed></ref>[Geman & Geman 1984]や、神経活動の事前分布としてスパース性を導入して自然画像を学習する事で、第一次視覚野の単純細胞の受容野の形成を説明したOlshausen & Fieldらの研究をその端緒として位置づけることができる<ref name=Geman1984><pubmed>22499653</pubmed></ref>[Olshausen 1996]。近年は、この生成モデル・ベイズの定理に基づく神経活動のモデリング・解析が盛んに行われている。詳しくは、予測符号化・自由エネルギー原理を参照のこと。 | |||
なお、本項目では神経符号化を刺激が神経活動に変換される過程としたが、広義にはこの過程には神経活動生成の基盤となるメカニズムの構築、すなわち刺激によるシナプス結合等の脳の構造の変化(学習・記憶)を含む。この場合、符号器として<math>p(x,w|y)</math>が使用され、生成モデルによるアプローチでは脳の構造も事後分布からのサンプリングとして形成されると考える。 | |||
==集団符号化== | ==集団符号化== | ||
神経細胞は集団で情報を符号化していると考えられるため、集団としての符号化方式を明らかにする事は神経符号化研究の中でも特に重要な課題になっている。神経細胞集団のどのような特徴によって情報が伝えられるかは、発火頻度による符号化と発火頻度以外の特徴量、特に同期的な活動(相関構造)による符号化も考慮する二つの立場がある。ここではより基本的な発火頻度に基づく集団符号化研究について紹介する。 | |||
===神経細胞の活動による刺激の弁別課題=== | ===神経細胞の活動による刺激の弁別課題=== | ||
集団符号化に対する重要な知見は少数の神経細胞の活動記録から得られている。サルMT野にあり、物体が特定の方向に動く時に反応する神経細胞を用いた実験結果が有名である<ref name=Britten1992><pubmed>1464765</pubmed></ref>[Britten 1992]。ランダムドットモーション視覚刺激をサルに提示し、ランダムに動くドットの何パーセントかが共通して特定の方向もしくはその反対方向を動くようにする。この向きは後で示すように同時に記録している運動方向選択性を有する神経細胞の選好方向もしくはその反対方向を使用する。このような条件で、Brittenらはどちら向きにドットの流れがあるかをサルに報告させ、共通して動くドットの割合を0%から100%まで変更したときの正答率を測定することで心理測定関数を得た。 | |||
ここでも神経符号化研究の方法論に従い、行動の成績と神経活動に基づく弁別課題の成績を比較する。すなわち、この課題を遂行中のサルのMT野から神経細胞活動を記録し、神経細胞の発火頻度から刺激(運動方向)の弁別を行う。驚くべきことに、このようにして得られた少数の神経細胞の活動に基づく弁別課題の成績は、行動成績に匹敵する。すなわち、この課題における動物の最終的な意思決定と行動は、MT野の多数の神経細胞の活動をもとにしていると考えられるのにもかかわらず、ごく僅かなMT野の神経細胞の活動によって説明されてしまう。電気生理実験による細胞外記録で記録される神経細胞は相当程度ランダムに選択されていることを考えれば、この事実はどのMT野神経細胞をとってきても行動を説明できること、すなわち行動に必要な情報はどのMT野神経細胞にも存在し、同じ情報が多数の神経細胞にシェアされていることを意味している。このような情報符号化方式を冗長符号化(redundant coding)という。 | |||
===チューニング関数と相関構造=== | ===チューニング関数と相関構造=== | ||
冗長符号化が実現されているという仮定のもとで次に問題となるのは、どのような神経活動によって、冗長性が実現されているのかという問題である。ZoharyらはMT野神経細胞が0。2程度の正の相関係数を示すことから、これが冗長性を生むと考えた<ref name=Zohary1994><pubmed>8022482</pubmed></ref>。例えば独立な神経細胞が2つあり、2つの発火頻度の平均値を刺激の推定量として使う場合、推定値の変動(分散)は1つの場合の半分になる。独立な神経細胞の5つの発火頻度の平均値で推定する場合は変動が5分の1になる。神経細胞の数を増やしていけば、推定値の変動を0に近くなるまでどこまでも小さくしていける。すなわち、神経細胞の数が多いほど推定精度は高くなる。ところが神経細胞の活動が正の相関を持つときには、推定精度に限界が生じる。MT野神経細胞集団のように相関係数が0。2である場合には、どんなに神経細胞の数を大きくしても、推定値の分散は1つの神経細胞の推定揺らぎの5分の1までしか小さくできない。刺激弁別の精度が神経細胞数の増加とともに一定の値に収束し、独立の場合よりずっと小さくなるのは冗長な符号化の一例となっている。 | |||
しかし、この考え方には大きな欠点がある。複数の神経細胞の活動の平均値を刺激の推定量とすることに意味があるのは、それら複数の神経細胞が刺激に対して全く同じように応答している場合のみである。すなわち、刺激と神経細胞の平均発火頻度との関係を表すチューニング関数(応答関数・活性化関数)が同じ神経細胞集団に対してのみ、発火頻度の平均値を推定量とすることに意味がある。しかし、一般には刺激の推定精度を議論するのに平均発火率の揺らぎを使用する妥当性はない。次に示すように、集団活動による刺激の推定精度は神経細胞間の相関だけで決められるわけではなく、個々の神経細胞のチューニング関数と相関構造の関係が重要な役割を担うことが明らかになっている<ref name=Averbeck2006><pubmed>16760916</pubmed></ref>。 | しかし、この考え方には大きな欠点がある。複数の神経細胞の活動の平均値を刺激の推定量とすることに意味があるのは、それら複数の神経細胞が刺激に対して全く同じように応答している場合のみである。すなわち、刺激と神経細胞の平均発火頻度との関係を表すチューニング関数(応答関数・活性化関数)が同じ神経細胞集団に対してのみ、発火頻度の平均値を推定量とすることに意味がある。しかし、一般には刺激の推定精度を議論するのに平均発火率の揺らぎを使用する妥当性はない。次に示すように、集団活動による刺激の推定精度は神経細胞間の相関だけで決められるわけではなく、個々の神経細胞のチューニング関数と相関構造の関係が重要な役割を担うことが明らかになっている<ref name=Averbeck2006><pubmed>16760916</pubmed></ref>[Averbeck 2006]。 | ||
[[ファイル:Shimazaki Neural Coding Fig2.png|サムネイル|'''図2. 2つの神経細胞の場合のシグナル相関とノイズ相関の関係'''<br>'''(A)''' チューニング関数が正のシグナル相関を持つ場合、正の2次相関により刺激の弁別が難しくなる。<br>'''(B)''' チューニング関数が負のシグナル相関を持つ場合、正の2次相関は刺激の弁別に影響しない。]] | [[ファイル:Shimazaki Neural Coding Fig2.png|サムネイル|'''図2. 2つの神経細胞の場合のシグナル相関とノイズ相関の関係'''<br>'''(A)''' チューニング関数が正のシグナル相関を持つ場合、正の2次相関により刺激の弁別が難しくなる。<br>'''(B)''' チューニング関数が負のシグナル相関を持つ場合、正の2次相関は刺激の弁別に影響しない。]] | ||
'''図2A、B'''の左のパネルは2つの神経細胞が類似したチューニング関数を持つ場合と性質の大きく異なるチューニング関数を持つ場合を示している。一方では、刺激が強くなると2つの神経細胞の発火頻度がともに大きくなる。他方では、2つのうち1つの神経細胞は刺激が強くなると発火頻度が小さくなる性質を持つ。2つの神経細胞の応答を各神経細胞の発火頻度を軸とする2次元の平面に描いたものが'''図2A、B''' | '''図2A、B'''の左のパネルは2つの神経細胞が類似したチューニング関数を持つ場合と性質の大きく異なるチューニング関数を持つ場合を示している。一方では、刺激が強くなると2つの神経細胞の発火頻度がともに大きくなる。他方では、2つのうち1つの神経細胞は刺激が強くなると発火頻度が小さくなる性質を持つ。2つの神経細胞の応答を各神経細胞の発火頻度を軸とする2次元の平面に描いたものが'''図2A、B'''の右パネルにある点線である。同様のチューニング関数の場合、2次元上の応答曲線は正の傾きを持つ。一方、反対のチューニング関数を持つ場合、応答曲線は負の傾きを持つ。このチューニング関数の相関をシグナル相関という。弱い刺激に対する応答の代表としてS1、強い刺激に対する応答としてS2の2点が描ける。 | ||
チューニング関数は各刺激の強さに対する神経細胞の平均発火頻度であり、実際には発火頻度は試行毎に異なる発火頻度が生成される。2つの神経細胞がある場合はこの生成は相関を伴うことがある。例えば、神経細胞の活動が正の相関を持つ場合には、一方の神経細胞が高い発火頻度を示した時にもう一方も高い発火頻度を示す。ある刺激が与えられたもとでの相関(共分散)をノイズ相関と呼ぶ。図2の右パネルの楕円は、刺激S1とS2が与えられた時に、神経活動が正の相関を持つ場合にサンプルが従う同時確率分布の等高線を描いており、その大きさはノイズの強さを表す。 | |||
= | 相関を伴う同時活動からS1とS2を弁別しようとするとき、2つの分布がなるべく重ならない状態であることが望ましい。そのような状態は当然、発火頻度の分散が小さい場合に実現されるが、ここでは個々の発火頻度の変動のレベルは一定とする(楕円の面積は変わらないとする)。このような時、ノイズ相関がどのように分布の重なりに影響を与えるかはシグナル相関に依存する。例えば'''図2A'''にあるように、2つの神経細胞が正のシグナル相関を持つ場合、正のノイズ相関があると分布の重なりは大きくなり弁別が難しくなる。もし負のノイズ相関を示す場合、分布の重なりは小さくなり弁別が容易になる。一方'''図2B'''にあるように、2つの神経細胞が負のシグナル相関を持つ場合、正の相関があると分布の重なりは小さくなり弁別が容易になる。もし負のノイズ相関があると分布の重なりは大きくなり弁別が難しくなる。すなわち、シグナル相関と反対のノイズ相関を持っている方が弁別は容易になる。一般に集団活動による刺激の弁別/推定の精度は神経細胞間の相関だけで決められるわけではなく、弁別/推定の方法と個々の神経細胞のチューニング関数および相関構造の関係において決まってくる。そのため神経細胞集団の正の相関活動が必ずしも推定に悪影響を与えるわけではない。これらの関係はKenneth O. Johnsonによって初めて数学的に示された<ref name=Johnson1980><pubmed>7411183</pubmed></ref>[Johnson 1980]。 | ||
==冗長性を生む相関構造の探索== | |||
こうした議論を3つ以上の神経細胞に拡張する場合、複数の神経細胞の活動から刺激を推定する際の推定値の精度を定量化することで明快に議論することができる。神経細胞集団による刺激の推定精度を用いることで、冗長な集団符号化を実現する相関構造を明らかにする試みが行われてきた。これらの研究は主に、サルやマウスの第一次視覚野の方位選択制細胞による、格子状刺激(grating stimulus)の方位の符号化を題材に行われている。 | |||
個々の神経細胞の発火頻度のみを使用して刺激の値を推定したい。これは、個々の神経細胞の発火頻度に重みをつけた線形関数で刺激の値を推定することで実現される。推定に最も適した重み付けがあり、そのような重みを持つ推定器を最適線形復号器(optimal linear decoder)という。この最適線形復号器の推定精度は線形フィッシャー情報量(linear Fisher information)によって与えられることが知られている。線形フィッシャー情報量はチューニング関数の刺激による微分と神経活動の相関(共分散行列)からなり、情報量はチューニング関数と活動相関の関係性において決定される事が示されている。線形フィッシャー情報量はまた、発火頻度の変化からごく僅かな刺激の変化を弁別するときの精度を表す。 | |||
AbbottとDayanは線形フィッシャー情報量を用いて、神経細胞がそれぞれ異なるチューニング関数を有するときに、一般に正の相関が情報量を下げたり、上限を与えるとは限らない事を示した<ref name=Abbott1999><pubmed>9950724</pubmed></ref>[Abbott 1999]。一方で、正の相関であってもより現実的な相関構造を仮定すると、これらはやはり情報量を下げる効果があることも示した。方位選択性細胞は同様の選好方向を持つ神経細胞同士の方が異なる選好方向を持つ神経細胞同士よりも強い正のノイズ相関を示す。このような相関の構造を制限範囲相関(limiting-range correlations)と呼ぶ。観測に即したこの制限範囲相関では相関が強いほど情報量が下がるが、数を増やしても一般には情報が制限されることはないことが示された。制限範囲相関はその後、釣鐘型の方位選択曲線と組み合わせて情報が制限される場合が詳しく調べられたが<ref name=Sompolinsky2001><pubmed>11735965</pubmed></ref>[Sompolinsky 2001]、より現実的に細胞ごとに幅や最大値の異なる非一様な方位選択曲線を想定すると、やはり制限範囲相関が必ずしも相関を下げる訳ではない事が示され<ref name=Ecker2011><pubmed>21976512</pubmed></ref>[Ecker 2010]、制限範囲相関が冗長性を生む機構であるとは断言できない状況となった<ref name=Kohn2016><pubmed>27145916</pubmed></ref>[Kohn 2016]。 | |||
== | 2014年にMoreno-Boteらは新たな理論を提出した。これによると、彼らが微分相関(differential correlations)と呼ぶ特定の相関がノイズ相関に少しでも存在すると、線形フィッシャー情報量は神経細胞の数が増えても必ず制限されることが示された<ref name=Moreno-Bote2014><pubmed>25195105</pubmed></ref>。それだけでなく、彼らは微分相関が唯一情報量を制限することのできる相関構造であると主張した。その後、微分相関が出現するメカニズムや実験データでの検証が始まった。特に2020年代から、数千の神経細胞から同時に記録を取ることができるようになり、実際に複数の脳領域で、情報量が制限されている様子を観測で確かめることができるようになってきた<ref name=Rumyantsev2020><pubmed>32238928</pubmed></ref><ref name=Bartolo2020><pubmed>31941667</pubmed></ref><ref name=Kafashan2021><pubmed>33473113</pubmed></ref>[Rumyantsev2020; Bartolo 2020; Kafashan 2021]。これらのデータ解析を通して、冗長符号化の実態が明らかになりつつある。 | ||
==参考文献== | ==参考文献== | ||
<references /> | <references /> | ||
2021年8月24日 (火) 11:50時点における版
北海道大学人間知・脳・AI研究教育センター 神経符号化
島崎秀昭
北海道大学人間知・脳・AI研究教育センター
DOI:10.14931/bsd.9895 原稿受付日:2021年8月3日 原稿完成日:2021年8月X日
担当編集委員:北城 圭一(生理学研究所)
同義語:神経コード
英:neural coding
神経符号化とは、外界の刺激が神経活動に変換・表現され、行動を担う神経活動が生成される過程を指す。刺激・行動と神経活動の関係を記述し、刺激の認識や行動生成を担う神経活動とその機構を同定することで、この過程を明らかにする研究を神経符号化研究(neural coding studies)という。同定された神経活動・機構を神経符号(neural code)と呼ぶ。
神経符号化とその研究方法
神経符号化は外界の刺激が神経活動に変換・表現され、行動を担う神経活動が生成される過程を指す。刺激の認識や行動生成を担う神経活動とそのメカニズムを同定することで、この過程を明らかにする研究を神経符号化研究という。具体的には、神経系のどの部位のどのタイプの神経細胞のどのような活動が、動物の認識・行動を説明するのに必要かつ十分であるかを明らかにすることで、外界の刺激が神経活動に変換され行動に至る過程を解明することを目指す研究領域である。Johns Hopkins大学のVernon Mountcastleは振動の感覚に関わる受容器を特定する次のような手法で、神経符号化研究の古典的な方法論を確立した[1][2] [Mountcastle 1972; カンデル神経科学2014]。
人間の手には圧力・振動・温度などの物理刺激に反応する12種類の受容器がある。特に指先には触覚に関わる4種類の機械受容器がある。表皮にあるマイスネル小体・メルケル受容器 、深皮にあるラフィニ終末・パチニ小体がそれである。これらの受容器は末梢神経細胞の軸索の終末にあり、そのもう一端は脊髄に投射する。脊髄の神経細胞から先は視床を介して体性感覚野に投射があり、我々の触知覚を担っている。4つの受容器は外界からの力の異なる特徴に対して反応し、順応特性が異なる。受容器が特定されているため、触覚に基づく我々の外界の認識がどの機械受容器を介した神経細胞の活動によって担われているかを問うことができる。
被験者(ヒトもしくはサル)に振動する物体を握らせ、振動の有無を報告させる。振動の振幅を変化させ、報告が可能な最小の振幅(閾値)を特定する。この作業を異なる振動数のもとで行うと、閾値は刺激の周波数に依存していることがわかる。次に同じ実験条件下で、機械受容器から投射する求心性繊維から電気記録を行うことで、振動に対する機械受容器の応答を記録し、神経活動が生じる振幅の閾値を調べる。すると、メルケル細胞の閾値は被験者の閾値よりもずっと高い位置にあり、被験者が振動を認識している状況でも活動をしていない状況があることがわかる。これにより、メルケル細胞の活動は振動の感覚を担う神経符号としては棄却される。一方、マイスネル小体・パチニ小体の閾値の周波数特性はそれぞれ低周波数(20-40Hz)・高周波数 (40-500Hz)での被験者のそれとほぼ一致することが示された。他の求心性繊維の活動は被験者の報告の結果を説明できないため、マイスネル小体・パチニ小体の活動が振動の感覚を担う神経符号であることが示された。
このように神経符号化研究では、観測者である動物に行動課題を課してそのパフォーマンスを計測する心理物理実験を行う。一方で同じ条件下で神経生理実験により神経活動を計測し、その活動から行動を予測する。そして両者の比較を行い動物の認識・行動を説明できる神経細胞・神経活動の候補を絞り込んでゆく。通常、前者は心理測定関数(psychometric function)、後者は神経測定関数(neurometric function)という形で記述される。図1に神経符号化研究の概略図を記した。ある神経細胞の特定の活動が動物の行動に必要な情報を担っている(神経符号の候補である)ためには、その神経活動の情報を用いて予測される最適な行動の成績が動物のそれを上回っていなければならない。そうでなければ、その神経細胞の活動は神経符号としては棄却される。なぜならば、行動に用いられた情報が神経活動として存在しているはずであり、その情報は計測した神経細胞もしくは行動予測に使用した活動特徴以外に存在しているはずだからである。
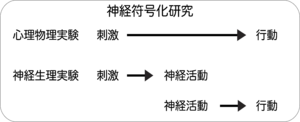
Johns Hopkins大学Kenneth O. Johnson氏による講義ノートより筆者が改変・加筆。
ここで注意すべきは、神経活動から予測される最適な行動に基づく心理実験課題の成績は実際に動物が行動によって報告した結果に基づく成績と同じである必要はなく、それを上回っていても良いことである。末梢神経等の初期段階で利用可能な情報が意思決定に余すとこなく使用されるとは限らないからである。しかしながら驚くべきことに、いくつかの事例において行動の成績が感覚受容器のパフォーマンスに接近していることが示されている。例えば人間は少なくとも数個の光子があればその報告が可能であると推定されており[3][4][5][Hecht 1942; Barlow 1956; Rieke 1998]、これは網膜視細胞の検出限界に近いと考えられている。これらの結果は、中枢神経系が効率的に入力情報を使用して行動を生成していることを示唆している[6][Barlow 1972]。一方、過去の知見に依存しない課題では、末梢神経のパフォーマンスを行動のパフォーマンスが上回ることはない。我々の認識精度の上限は感覚デバイスの精度に制限され、それを上回ることはないからである。
もちろん、このような古典的な神経符号化研究の手法で行動を担う神経細胞を明快に特定できるのは、行動に必要な信号の通る経路が明らかだからである。これ以外の状況では、たとえ神経細胞から行動を予測できたとしても、行動がその部位の活動に依存すると断定することはできない。そのため損傷実験や電気刺激・光遺伝学による介入実験と組み合わせる事で、行動を担う神経活動を明らかにする事が試みられている。
Mountcastleらの神経符号化研究では神経活動から刺激の有無を推定する復号化の手法が用いられるが、刺激が神経活動へどのように変換されるかを表す符号化の方式を明らかにする事は神経符号化研究における主要な課題である。神経符号化は神経系における情報の変換と表現を指すともされ[7][Perkel and Bullock 1968]、それぞれ符号化・復号化の手法を用いて情報神経細胞が担う情報を明らかにすることが試みられている。詳しくは次節の符号化・復号化の項目で述べる。近年では入力刺激から意思決定までをいわゆるend-to-endで実装した深層ニューラルネットワークが人間のパフォーマンスを上回ったことから、深層ニューラルネットワークの各層と脳の領野の活動を比較する新しいタイプの神経符号化研究も生まれている[8][Yamins 2014]。
符号化と復号化
符号化と復号化は情報理論の用語で、文字・画像・音声などを送信者から通信路を介して受信者に伝達するために、送信者側で情報源・通信路に適した形に変換し、受信者側でそれを元に戻すことを指す。そのために用いられる機器あるいはアルゴリズムを符号器(エンコーダ)・復号器(デコーダ)と呼ぶ。神経科学の文脈では、符号化は刺激が神経活動に変換されることに対応し、刺激が与えられたもとで神経細胞の活動を表すモデルを符号器、神経活動が与えられたもとで刺激を表すモデルを復号器と呼ぶ。多くの場合、これらは統計モデルを用いて記述される。統計モデルによって符号器・復号器を記述することで、神経発火活動のどの特徴に情報があるかを調べる事ができる。以下に、神経符号化研究で用いられる符号化・復号化のアプローチを紹介する。
神経科学における符号化は外界の刺激を神経活動に変換する過程・機構を言う。単一神経細胞の発火頻度と刺激の関係を表す関数(チューニング関数・応答関数・活性化関数)は符号器の例であり、これらを組み合わせた人工ニューラルネットワークも符号器である。応答の確率的揺らぎも考慮すると、平均値がチューニング関数で与えられる確率分布が符号器となる。ただし、一般には平均発火頻度に限らず刺激に依存する神経活動を確率分布で表したものが符号器となる。複数の神経細胞による集団符号化の議論では、刺激に依存する神経活動の同時確率分布が符号器となる。 個の神経細胞集団の活動をで表し刺激をで表すと、同時確率分布はと書くことができる。ただし、は分布のパラメータである。例えば神経活動として発火頻度を取り上げ、試行毎の実現にガウスノイズを仮定して神経活動を近似する場合には多変量正規分布が符号器となり、平均発火頻度もしくは共分散行列、あるいはその両方が刺激に依存する。神経スパイク活動に対しては刺激依存のパラメータを有する点過程モデルやイジングモデルを用いた集団活動の同時分布が符号器となる。
神経符号化研究では、神経細胞の活動のどの部分に外界の情報が表され、運ばれているのかを特定することが重要な課題になる。この課題に統計モデルを使用することのメリットは、使用するデータの特徴がモデルの十分統計量として厳密に定義される点にある。神経活動のどの特徴が外界に依存し、外界の変化とともに変わるのかについて複数の仮説が考えられる。代表的な例として、単一神経細胞の発火頻度によって刺激が符号化されるとする発火頻度符号化(rate coding)、神経スパイクの時間構造に刺激が符号化されているとする時間的符号化(temporal coding)、相関を伴う神経細胞集団の同時活動に刺激が符号化されているとする集団符号化(population coding)等が挙げられる。これらはそれぞれ符号器としてポアソン過程、非ポアソン過程、多変量ガウス分布/イジングモデル/一般化線形モデルを用いてモデル化することができ、仮説を数学的に明らかな形で取り扱うことができる。次節では、これらのうち神経符号化研究で中心的な役割を担う集団符号化について詳しく述べる。
神経細胞による符号化の実現を考えるとき、下流の神経細胞がこれらの特徴を読み取ることができるか、すなわち符号化に用いる神経活動の特徴量の変化に応じて下流の神経細胞が活動を変えることができるかを考える必要がある。個々のシナプス前細胞の発火頻度に応じてシナプス後細胞の活動が変化することは容易に実現できるため、発火頻度を神経符号の仮説として採用することが多い。しかし、樹状突起上の電位依存性チャネルによる非線形な応答を考慮すれば、シナプス入力時系列の時間構造や同期的なシナプス入力などの2次以上の統計量に依存してシナプス後細胞が活動することも容易に考えられる。そのため神経細胞によって応答が可能(符号化が可能)な特徴量を実験的・理論的に考察する事が行われてきた[9][10][Diesmann 1999; De La Rocha 2007]。実際、発火頻度符号化以外の符号化方式の存在も報告されており[11][12][Ishikane 2005; Jacobs 2009]、神経系は単一の符号化方式を採用するのではなく種や部位により異なる符号化方式が採用されていると考えられている。
神経符号化研究では、神経活動から刺激や行動の意図等を推定する復号器を構築・適用することで神経細胞が保持する情報を明らかにすることが行われる。復号器の構築方法には2通りの方法がある。一つ目は復号器を神経細胞の活動から直接的に作る方法である。例として、神経活動の重み付け線形和によって刺激を推定する線形モデルが挙げられる。この方法の拡張として、刺激の分布として指数分布族を用い、その期待値を連結関数を通して神経細胞活動の線形和で表す一般化線形モデルがある。これらは確率モデルを直接構成する方法である。二つ目の方法は、符号化で用いたモデルを使用し、符号器のパラメータ推定として刺激を推定する方法である。例えば、符号器を用いた尤度関数を使って刺激の最尤推定を行うことは復号化にあたる。この方法は刺激に対して事前分布を仮定することで、ベイズの定理を用いた事後分布による刺激の推定に一般化される。
このように復号器を符号化のモデルから作成する方法を2段階法(two step approach)と呼ぶ[13][Brown 2004]。
外界の刺激がスムーズに変化するなど、時系列になんらかの仮定をする場合、神経活動は状態空間モデルで記述される。状態空間モデルに基づく刺激の推定は、ベイズ推定を逐次的に行う逐次ベイズ推定技術を用いて解くことができる。Brownらはラットの海馬神経細胞の場所細胞の活動からラットの位置をデコードする方法として、符号器として点過程を用い、事前分布として位置が線形の状態遷移すると仮定した2段階法を用いて、海馬場所細胞のスパイク時系列からラットの位置のスムーズなデコーディングを初めて実現した[13][Brown 1998]。神経スパイクに対するこのような非ガウスのフィルタリング技術はブレーン・マシーン・インターフェースやブレーン・コンピュータ・インターフェースと呼ばれる神経補綴技術の基盤技術として幅広く使用されている。
ただし復号化で使用する神経活動の特徴量が複雑になってきた場合、その特徴に下流の神経細胞が反応する事は困難である事が予想される。そのため高度な神経補綴に用いられる神経活動がそのまま行動に繋がる神経符号として採用されるわけではない。また厳密には、こうして特定された神経細胞活動が行動に関わるかを調べるためには、これらの細胞を選択的に制御して行動に影響があるかを調べる必要がある。
最後に、符号器にも2通りの構築方法があることを紹介する。初めに紹介したように符号器として神経細胞が刺激に応答するモデルを直接構築する方法のほかに、符号器をベイズの定理を用いて表す方法がある。これを用いると符号器は復号器を用いて次のように表される。
ここでパラメータは神経活動を生成する基盤としての脳の構造を表す。は神経活動に対する事前分布で神経活動に対する制約条件を表す。また、ここでの復号器は神経細胞活動による外界の表現/表象(representation)を記述する。事前分布と復号器を合わせた同時分布をデータの生成モデルと呼ぶ。生成モデルはデータyが生成される過程を神経活動によって再現するモデルと見做す事ができる。従ってこの式は、刺激に対する神経細胞集団の応答活動をデータ生成のモデルによって解釈することができることを示している。
これによれば、脳の内部構造に基づく神経細胞の自発活動、すなわち脳の内発的ダイナミクスは事前分布を構成する。刺激が提示されると、神経活動は刺激の影響を受けて変調され、復号器と組み合わされて事後分布を形成する[14] [15][Fiser 2010; Berkes 2011]。すなわち神経応答活動は刺激を再構成・予測するための推論を行なっていると考える事ができる。神経応答活動のベイズ的な見方によれば、脳内に刺激を推定する復号器の存在を陽に仮定する必要はなくなり、復号器の役割は自発活動から刺激応答活動への変化に内包される。
生成モデルに基づく符号化研究は、正則化を課した画像の再構成という視覚野の計算論に関わる研究をその祖として古くから行われ、マルコフ確率場を用いたGeman & Gemanらによる画像再構成[16][Geman & Geman 1984]や、神経活動の事前分布としてスパース性を導入して自然画像を学習する事で、第一次視覚野の単純細胞の受容野の形成を説明したOlshausen & Fieldらの研究をその端緒として位置づけることができる[16][Olshausen 1996]。近年は、この生成モデル・ベイズの定理に基づく神経活動のモデリング・解析が盛んに行われている。詳しくは、予測符号化・自由エネルギー原理を参照のこと。
なお、本項目では神経符号化を刺激が神経活動に変換される過程としたが、広義にはこの過程には神経活動生成の基盤となるメカニズムの構築、すなわち刺激によるシナプス結合等の脳の構造の変化(学習・記憶)を含む。この場合、符号器としてが使用され、生成モデルによるアプローチでは脳の構造も事後分布からのサンプリングとして形成されると考える。
集団符号化
神経細胞は集団で情報を符号化していると考えられるため、集団としての符号化方式を明らかにする事は神経符号化研究の中でも特に重要な課題になっている。神経細胞集団のどのような特徴によって情報が伝えられるかは、発火頻度による符号化と発火頻度以外の特徴量、特に同期的な活動(相関構造)による符号化も考慮する二つの立場がある。ここではより基本的な発火頻度に基づく集団符号化研究について紹介する。
神経細胞の活動による刺激の弁別課題
集団符号化に対する重要な知見は少数の神経細胞の活動記録から得られている。サルMT野にあり、物体が特定の方向に動く時に反応する神経細胞を用いた実験結果が有名である[17][Britten 1992]。ランダムドットモーション視覚刺激をサルに提示し、ランダムに動くドットの何パーセントかが共通して特定の方向もしくはその反対方向を動くようにする。この向きは後で示すように同時に記録している運動方向選択性を有する神経細胞の選好方向もしくはその反対方向を使用する。このような条件で、Brittenらはどちら向きにドットの流れがあるかをサルに報告させ、共通して動くドットの割合を0%から100%まで変更したときの正答率を測定することで心理測定関数を得た。
ここでも神経符号化研究の方法論に従い、行動の成績と神経活動に基づく弁別課題の成績を比較する。すなわち、この課題を遂行中のサルのMT野から神経細胞活動を記録し、神経細胞の発火頻度から刺激(運動方向)の弁別を行う。驚くべきことに、このようにして得られた少数の神経細胞の活動に基づく弁別課題の成績は、行動成績に匹敵する。すなわち、この課題における動物の最終的な意思決定と行動は、MT野の多数の神経細胞の活動をもとにしていると考えられるのにもかかわらず、ごく僅かなMT野の神経細胞の活動によって説明されてしまう。電気生理実験による細胞外記録で記録される神経細胞は相当程度ランダムに選択されていることを考えれば、この事実はどのMT野神経細胞をとってきても行動を説明できること、すなわち行動に必要な情報はどのMT野神経細胞にも存在し、同じ情報が多数の神経細胞にシェアされていることを意味している。このような情報符号化方式を冗長符号化(redundant coding)という。
チューニング関数と相関構造
冗長符号化が実現されているという仮定のもとで次に問題となるのは、どのような神経活動によって、冗長性が実現されているのかという問題である。ZoharyらはMT野神経細胞が0。2程度の正の相関係数を示すことから、これが冗長性を生むと考えた[18]。例えば独立な神経細胞が2つあり、2つの発火頻度の平均値を刺激の推定量として使う場合、推定値の変動(分散)は1つの場合の半分になる。独立な神経細胞の5つの発火頻度の平均値で推定する場合は変動が5分の1になる。神経細胞の数を増やしていけば、推定値の変動を0に近くなるまでどこまでも小さくしていける。すなわち、神経細胞の数が多いほど推定精度は高くなる。ところが神経細胞の活動が正の相関を持つときには、推定精度に限界が生じる。MT野神経細胞集団のように相関係数が0。2である場合には、どんなに神経細胞の数を大きくしても、推定値の分散は1つの神経細胞の推定揺らぎの5分の1までしか小さくできない。刺激弁別の精度が神経細胞数の増加とともに一定の値に収束し、独立の場合よりずっと小さくなるのは冗長な符号化の一例となっている。
しかし、この考え方には大きな欠点がある。複数の神経細胞の活動の平均値を刺激の推定量とすることに意味があるのは、それら複数の神経細胞が刺激に対して全く同じように応答している場合のみである。すなわち、刺激と神経細胞の平均発火頻度との関係を表すチューニング関数(応答関数・活性化関数)が同じ神経細胞集団に対してのみ、発火頻度の平均値を推定量とすることに意味がある。しかし、一般には刺激の推定精度を議論するのに平均発火率の揺らぎを使用する妥当性はない。次に示すように、集団活動による刺激の推定精度は神経細胞間の相関だけで決められるわけではなく、個々の神経細胞のチューニング関数と相関構造の関係が重要な役割を担うことが明らかになっている[19][Averbeck 2006]。

(A) チューニング関数が正のシグナル相関を持つ場合、正の2次相関により刺激の弁別が難しくなる。
(B) チューニング関数が負のシグナル相関を持つ場合、正の2次相関は刺激の弁別に影響しない。
図2A、Bの左のパネルは2つの神経細胞が類似したチューニング関数を持つ場合と性質の大きく異なるチューニング関数を持つ場合を示している。一方では、刺激が強くなると2つの神経細胞の発火頻度がともに大きくなる。他方では、2つのうち1つの神経細胞は刺激が強くなると発火頻度が小さくなる性質を持つ。2つの神経細胞の応答を各神経細胞の発火頻度を軸とする2次元の平面に描いたものが図2A、Bの右パネルにある点線である。同様のチューニング関数の場合、2次元上の応答曲線は正の傾きを持つ。一方、反対のチューニング関数を持つ場合、応答曲線は負の傾きを持つ。このチューニング関数の相関をシグナル相関という。弱い刺激に対する応答の代表としてS1、強い刺激に対する応答としてS2の2点が描ける。
チューニング関数は各刺激の強さに対する神経細胞の平均発火頻度であり、実際には発火頻度は試行毎に異なる発火頻度が生成される。2つの神経細胞がある場合はこの生成は相関を伴うことがある。例えば、神経細胞の活動が正の相関を持つ場合には、一方の神経細胞が高い発火頻度を示した時にもう一方も高い発火頻度を示す。ある刺激が与えられたもとでの相関(共分散)をノイズ相関と呼ぶ。図2の右パネルの楕円は、刺激S1とS2が与えられた時に、神経活動が正の相関を持つ場合にサンプルが従う同時確率分布の等高線を描いており、その大きさはノイズの強さを表す。
相関を伴う同時活動からS1とS2を弁別しようとするとき、2つの分布がなるべく重ならない状態であることが望ましい。そのような状態は当然、発火頻度の分散が小さい場合に実現されるが、ここでは個々の発火頻度の変動のレベルは一定とする(楕円の面積は変わらないとする)。このような時、ノイズ相関がどのように分布の重なりに影響を与えるかはシグナル相関に依存する。例えば図2Aにあるように、2つの神経細胞が正のシグナル相関を持つ場合、正のノイズ相関があると分布の重なりは大きくなり弁別が難しくなる。もし負のノイズ相関を示す場合、分布の重なりは小さくなり弁別が容易になる。一方図2Bにあるように、2つの神経細胞が負のシグナル相関を持つ場合、正の相関があると分布の重なりは小さくなり弁別が容易になる。もし負のノイズ相関があると分布の重なりは大きくなり弁別が難しくなる。すなわち、シグナル相関と反対のノイズ相関を持っている方が弁別は容易になる。一般に集団活動による刺激の弁別/推定の精度は神経細胞間の相関だけで決められるわけではなく、弁別/推定の方法と個々の神経細胞のチューニング関数および相関構造の関係において決まってくる。そのため神経細胞集団の正の相関活動が必ずしも推定に悪影響を与えるわけではない。これらの関係はKenneth O. Johnsonによって初めて数学的に示された[20][Johnson 1980]。
冗長性を生む相関構造の探索
こうした議論を3つ以上の神経細胞に拡張する場合、複数の神経細胞の活動から刺激を推定する際の推定値の精度を定量化することで明快に議論することができる。神経細胞集団による刺激の推定精度を用いることで、冗長な集団符号化を実現する相関構造を明らかにする試みが行われてきた。これらの研究は主に、サルやマウスの第一次視覚野の方位選択制細胞による、格子状刺激(grating stimulus)の方位の符号化を題材に行われている。
個々の神経細胞の発火頻度のみを使用して刺激の値を推定したい。これは、個々の神経細胞の発火頻度に重みをつけた線形関数で刺激の値を推定することで実現される。推定に最も適した重み付けがあり、そのような重みを持つ推定器を最適線形復号器(optimal linear decoder)という。この最適線形復号器の推定精度は線形フィッシャー情報量(linear Fisher information)によって与えられることが知られている。線形フィッシャー情報量はチューニング関数の刺激による微分と神経活動の相関(共分散行列)からなり、情報量はチューニング関数と活動相関の関係性において決定される事が示されている。線形フィッシャー情報量はまた、発火頻度の変化からごく僅かな刺激の変化を弁別するときの精度を表す。
AbbottとDayanは線形フィッシャー情報量を用いて、神経細胞がそれぞれ異なるチューニング関数を有するときに、一般に正の相関が情報量を下げたり、上限を与えるとは限らない事を示した[21][Abbott 1999]。一方で、正の相関であってもより現実的な相関構造を仮定すると、これらはやはり情報量を下げる効果があることも示した。方位選択性細胞は同様の選好方向を持つ神経細胞同士の方が異なる選好方向を持つ神経細胞同士よりも強い正のノイズ相関を示す。このような相関の構造を制限範囲相関(limiting-range correlations)と呼ぶ。観測に即したこの制限範囲相関では相関が強いほど情報量が下がるが、数を増やしても一般には情報が制限されることはないことが示された。制限範囲相関はその後、釣鐘型の方位選択曲線と組み合わせて情報が制限される場合が詳しく調べられたが[22][Sompolinsky 2001]、より現実的に細胞ごとに幅や最大値の異なる非一様な方位選択曲線を想定すると、やはり制限範囲相関が必ずしも相関を下げる訳ではない事が示され[23][Ecker 2010]、制限範囲相関が冗長性を生む機構であるとは断言できない状況となった[24][Kohn 2016]。
2014年にMoreno-Boteらは新たな理論を提出した。これによると、彼らが微分相関(differential correlations)と呼ぶ特定の相関がノイズ相関に少しでも存在すると、線形フィッシャー情報量は神経細胞の数が増えても必ず制限されることが示された[25]。それだけでなく、彼らは微分相関が唯一情報量を制限することのできる相関構造であると主張した。その後、微分相関が出現するメカニズムや実験データでの検証が始まった。特に2020年代から、数千の神経細胞から同時に記録を取ることができるようになり、実際に複数の脳領域で、情報量が制限されている様子を観測で確かめることができるようになってきた[26][27][28][Rumyantsev2020; Bartolo 2020; Kafashan 2021]。これらのデータ解析を通して、冗長符号化の実態が明らかになりつつある。
参考文献
- ↑
Mountcastle, V.B., LaMotte, R.H., & Carli, G. (1972).
Detection thresholds for stimuli in humans and monkeys: comparison with threshold events in mechanoreceptive afferent nerve fibers innervating the monkey hand. Journal of neurophysiology, 35(1), 122-36. [PubMed:4621505] [WorldCat] [DOI] - ↑ 日本語版監修 金澤一郎・宮下保司 (2014).
カンデル神経科学第5版 第21章感覚の符号化・第23章触覚 メディカル・サイエンス・インターナショナル社 - ↑
Hecht, S., Shlaer, S., & Pirenne, M.H. (1942).
ENERGY, QUANTA, AND VISION. The Journal of general physiology, 25(6), 819-40. [PubMed:19873316] [PMC] [WorldCat] [DOI] - ↑
BARLOW, H.B. (1956).
Retinal noise and absolute threshold. Journal of the Optical Society of America, 46(8), 634-9. [PubMed:13346424] [WorldCat] [DOI] - ↑ Rieke, F. & Baylor, D. A. (1998)
Single-photon detection by rod cells of the retina. Reviews of Modern Physics. 70(3):1027 - ↑
Barlow, H.B. (1972).
Single units and sensation: a neuron doctrine for perceptual psychology? Perception, 1(4), 371-94. [PubMed:4377168] [WorldCat] [DOI] - ↑ Perkel, D. H. & Bullock, T. H. (1968).
Neural coding. Neurosciences Research Program Bulletin - ↑
Yamins, D.L., Hong, H., Cadieu, C.F., Solomon, E.A., Seibert, D., & DiCarlo, J.J. (2014).
Performance-optimized hierarchical models predict neural responses in higher visual cortex. Proceedings of the National Academy of Sciences of the United States of America, 111(23), 8619-24. [PubMed:24812127] [PMC] [WorldCat] [DOI] - ↑
Diesmann, M., Gewaltig, M.O., & Aertsen, A. (1999).
Stable propagation of synchronous spiking in cortical neural networks. Nature, 402(6761), 529-33. [PubMed:10591212] [WorldCat] [DOI] - ↑
de la Rocha, J., Doiron, B., Shea-Brown, E., Josić, K., & Reyes, A. (2007).
Correlation between neural spike trains increases with firing rate. Nature, 448(7155), 802-6. [PubMed:17700699] [WorldCat] [DOI] - ↑
Ishikane, H., Gangi, M., Honda, S., & Tachibana, M. (2005).
Synchronized retinal oscillations encode essential information for escape behavior in frogs. Nature neuroscience, 8(8), 1087-95. [PubMed:15995702] [WorldCat] [DOI] - ↑
Jacobs, A.L., Fridman, G., Douglas, R.M., Alam, N.M., Latham, P.E., Prusky, G.T., & Nirenberg, S. (2009).
Ruling out and ruling in neural codes. Proceedings of the National Academy of Sciences of the United States of America, 106(14), 5936-41. [PubMed:19297621] [PMC] [WorldCat] [DOI] - ↑ 13.0 13.1
Brown, E.N., Kass, R.E., & Mitra, P.P. (2004).
Multiple neural spike train data analysis: state-of-the-art and future challenges. Nature neuroscience, 7(5), 456-61. [PubMed:15114358] [WorldCat] [DOI] - ↑
Brown, E.N., Frank, L.M., Tang, D., Quirk, M.C., & Wilson, M.A. (1998).
A statistical paradigm for neural spike train decoding applied to position prediction from ensemble firing patterns of rat hippocampal place cells. The Journal of neuroscience : the official journal of the Society for Neuroscience, 18(18), 7411-25. [PubMed:9736661] [PMC] [WorldCat] - ↑
Fiser, J., Berkes, P., Orbán, G., & Lengyel, M. (2010).
Statistically optimal perception and learning: from behavior to neural representations. Trends in cognitive sciences, 14(3), 119-30. [PubMed:20153683] [PMC] [WorldCat] [DOI] - ↑ 16.0 16.1
Geman, S., & Geman, D. (1984).
Stochastic relaxation, gibbs distributions, and the bayesian restoration of images. IEEE transactions on pattern analysis and machine intelligence, 6(6), 721-41. [PubMed:22499653] [WorldCat] [DOI] - ↑
Britten, K.H., Shadlen, M.N., Newsome, W.T., & Movshon, J.A. (1992).
The analysis of visual motion: a comparison of neuronal and psychophysical performance. The Journal of neuroscience : the official journal of the Society for Neuroscience, 12(12), 4745-65. [PubMed:1464765] [WorldCat] - ↑
Zohary, E., Shadlen, M.N., & Newsome, W.T. (1994).
Correlated neuronal discharge rate and its implications for psychophysical performance. Nature, 370(6485), 140-3. [PubMed:8022482] [WorldCat] [DOI] - ↑
Averbeck, B.B., Latham, P.E., & Pouget, A. (2006).
Neural correlations, population coding and computation. Nature reviews. Neuroscience, 7(5), 358-66. [PubMed:16760916] [WorldCat] [DOI] - ↑
Johnson, K.O. (1980).
Sensory discrimination: neural processes preceding discrimination decision. Journal of neurophysiology, 43(6), 1793-815. [PubMed:7411183] [WorldCat] [DOI] - ↑
Abbott, L.F., & Dayan, P. (1999).
The effect of correlated variability on the accuracy of a population code. Neural computation, 11(1), 91-101. [PubMed:9950724] [WorldCat] [DOI] - ↑
Sompolinsky, H., Yoon, H., Kang, K., & Shamir, M. (2001).
Population coding in neuronal systems with correlated noise. Physical review. E, Statistical, nonlinear, and soft matter physics, 64(5 Pt 1), 051904. [PubMed:11735965] [WorldCat] [DOI] - ↑
Ecker, A.S., Berens, P., Tolias, A.S., & Bethge, M. (2011).
The effect of noise correlations in populations of diversely tuned neurons. The Journal of neuroscience : the official journal of the Society for Neuroscience, 31(40), 14272-83. [PubMed:21976512] [PMC] [WorldCat] [DOI] - ↑
Kohn, A., Coen-Cagli, R., Kanitscheider, I., & Pouget, A. (2016).
Correlations and Neuronal Population Information. Annual review of neuroscience, 39, 237-56. [PubMed:27145916] [PMC] [WorldCat] [DOI] - ↑
Moreno-Bote, R., Beck, J., Kanitscheider, I., Pitkow, X., Latham, P., & Pouget, A. (2014).
Information-limiting correlations. Nature neuroscience, 17(10), 1410-7. [PubMed:25195105] [PMC] [WorldCat] [DOI] - ↑
Rumyantsev, O.I., Lecoq, J.A., Hernandez, O., Zhang, Y., Savall, J., Chrapkiewicz, R., ..., & Schnitzer, M.J. (2020).
Fundamental bounds on the fidelity of sensory cortical coding. Nature, 580(7801), 100-105. [PubMed:32238928] [WorldCat] [DOI] - ↑
Bartolo, R., Saunders, R.C., Mitz, A.R., & Averbeck, B.B. (2020).
Information-Limiting Correlations in Large Neural Populations. The Journal of neuroscience : the official journal of the Society for Neuroscience, 40(8), 1668-1678. [PubMed:31941667] [PMC] [WorldCat] [DOI] - ↑
Kafashan, M., Jaffe, A.W., Chettih, S.N., Nogueira, R., Arandia-Romero, I., Harvey, C.D., ..., & Drugowitsch, J. (2021).
Scaling of sensory information in large neural populations shows signatures of information-limiting correlations. Nature communications, 12(1), 473. [PubMed:33473113] [PMC] [WorldCat] [DOI]












