「積分発火モデル」の版間の差分
細編集の要約なし |
|||
| (同じ利用者による、間の4版が非表示) | |||
| 8行目: | 8行目: | ||
担当編集委員:[http://researchmap.jp/123qweasd 五味 裕章](NTTコミュニケーション科学基礎研究所 人間情報研究部)<br> | 担当編集委員:[http://researchmap.jp/123qweasd 五味 裕章](NTTコミュニケーション科学基礎研究所 人間情報研究部)<br> | ||
</div> | </div> | ||
{{box|text= 積分発火モデルは、神経細胞の電気活動を数理的に記述するモデルの1つである。神経細胞の電気的状態を膜電位により表し、神経細胞の出力である活動電位 (スパイク) の生成過程の記述を省略し、活動電位の閾値以下の範囲における膜電位の変化を微分方程式により記述する。活動電位の生成機構もモデル化するHodgkin-Huxleyモデルよりも計算コストが少ないため、膜電位変化を記述する神経細胞モデルとして、広く用いられている。}} | {{box|text= 積分発火モデルは、神経細胞の電気活動を数理的に記述するモデルの1つである。神経細胞の電気的状態を膜電位により表し、神経細胞の出力である活動電位 (スパイク) の生成過程の記述を省略し、活動電位の閾値以下の範囲における膜電位の変化を微分方程式により記述する。活動電位の生成機構もモデル化するHodgkin-Huxleyモデルよりも計算コストが少ないため、膜電位変化を記述する神経細胞モデルとして、広く用いられている。}} | ||
==はじめに== | ==はじめに== | ||
神経細胞の電気的特性については、HodgkinとHuxleyによって細胞膜上に発現しているイオンチャネルの膜電位依存性とそれらによる活動電位生成機構、およびその数理的な表現が明らかにされたが<ref name=Hodgkin1952><pubmed>12991237</pubmed></ref>[1]、それ以前にLapicqueによって、細胞膜のキャパシタとしての特性や神経興奮現象(活動電位生成)に対する閾値となる電位、および、閾値に到るまでの過程について詳細に調べられていた<ref name=Lapicque1907>'''Lapicque, L. (1907).'''<br>Recherches quantitatives sur l'excitation électrique des nerfs traitée comme une polarization. Journal de physiologie et de pathologie générale, 9, 620-635.</ref><ref name=Lapicque2007><pubmed>18046573</pubmed></ref> [2,3]。入力として与えられた電流はキャパシタとしての特性により膜電位に積算(integrate)される。膜電位が上昇して閾値に到達すると、活動電位を発生(fire)する。この膜電位の閾値に達するまでの積算過程をモデル化したのが、積分発火モデルである。このモデルでは活動電位生成中の膜電位変動は記述しない。それは非常に短時間(< 2msec)の過程であり、膜電位挙動のほとんどの時間が閾値に到るまでの積算過程であるとみなせるためである。神経細胞の状態を表す変数が膜電位のみの1変数であるため、計算量も多くない。このため、多くの研究において、採用されてきたモデルである。一方で、神経細胞応答の本質であるアクティブな膜伝導性を一切無視したモデルであるため、実際の神経細胞応答とは異なる特性を示すことから、その拡張モデルも多く提案されてきた。以下では、まず、基本となる積分発火モデルであるLeaky Integrate-and-Fireモデル(LIFモデル、と呼ばれる)を解説し、次にその拡張モデルとして代表的なものを紹介する。 | |||
[[ファイル:Kitano 積分発火モデルFig1.png|サムネイル|450px|'''図1. 積分発火モデルとMulti-timescale Adaptive Threshold (MAT)モデル(拡張された積分発火モデルを参照)の模式図''' | [[ファイル:Kitano 積分発火モデルFig1.png|サムネイル|450px|'''図1. 積分発火モデルとMulti-timescale Adaptive Threshold (MAT)モデル(拡張された積分発火モデルを参照)の模式図''' | ||
| 23行目: | 19行目: | ||
'''B.''' Multi-timescale Adaptive Thresholdモデル:スパイクを生成すると、膜電位をリセットせずに閾値 (マゼンタ) を変動させる。閾値パラメータは<math>\omega=10\mbox{ }[mV]</math>, <math>\alpha_1=4\mbox{ }[mV]</math>, <math>\alpha_2=3\mbox{ }[mV]</math>である。その他 のパラメータは<math>\tau_m=5\mbox{ }[ms]</math>, <math>R_m=10\mbox{ }[M\Omega]</math>, <math>E_L=0\mbox{ }[mV]</math>である。]] | '''B.''' Multi-timescale Adaptive Thresholdモデル:スパイクを生成すると、膜電位をリセットせずに閾値 (マゼンタ) を変動させる。閾値パラメータは<math>\omega=10\mbox{ }[mV]</math>, <math>\alpha_1=4\mbox{ }[mV]</math>, <math>\alpha_2=3\mbox{ }[mV]</math>である。その他 のパラメータは<math>\tau_m=5\mbox{ }[ms]</math>, <math>R_m=10\mbox{ }[M\Omega]</math>, <math>E_L=0\mbox{ }[mV]</math>である。]] | ||
== | == 積分発火モデル == | ||
Integrate and fire model | |||
脂質二重層からなる神経細胞の細胞膜により、電荷をもつイオンは細胞膜からの流出入を妨げてられている。細胞外の電位を基準電位 (0 mV) とした場合、細胞内の電位を表す膜電位は、通常、負の値をもつ過分極した状態(およそ–70 mV付近)をとる。神経細胞は、細胞膜の外側と内側にそれぞれ正の電荷および負の電荷をもつイオンを帯電させた状態になり、細胞膜はキャパシタの性質を有する。細胞膜上に発現したタンパク質であるイオンチャネルが、その状態によってイオンの流出入を促す場合があり、膜電位の変化をもたらす。膜電位を<math>V</math>とし、細胞膜の膜容量を<math>C_m</math>、細胞膜(実際にはイオンチャンネル)を透過する電流 (膜電流) を<math>I_m</math>とすると、 | |||
::<math>C_m\frac{dV}{dt}=-I_m</math> | ::<math>C_m\frac{dV}{dt}=-I_m</math> | ||
| 34行目: | 32行目: | ||
のように書ける。 | のように書ける。 | ||
膜電流<math>I_m</math> | 膜電流<math>I_m</math>は、細胞膜上に発現するイオンチャネルを透過する電流を表す。イオンチャネルは、典型的には10種類程度発現し、それぞれ異なる特性を有する。各イオンチャネルを透過する電流のコンダクタンス(あるいは、その逆数の抵抗)は、膜電位に依存して変化するアクティブな性質をもち、この性質によりパルス状の膜電位変化である活動電位が生成される。しかし、活動電位は、膜電位が閾値と呼ばれるレベルまで上昇すると、そこからさらに急速に上昇して正の電位に到達後、急速に下降して閾値以下の過分極したレベルまで戻る(リセットと呼ぶ)という定型の変化を示すことから、活動電位生成中の変化は省略し、リセット後から閾値到達までの変化のみを定式化する。膜電流としては、アクティブな伝導性を無視し、伝導性の時間に不変な成分を括り出したリーク電流のみを採用する。リーク電流は、時間に不変なコンダクタンスを<math>G_L</math>、この電流の反転電位を<math>E_L</math>とすると、 | ||
::<math>I_m=G_L(V-E_L)</math> | ::<math>I_m=G_L(V-E_L)</math> | ||
と表すことができる。これに加え、膜電位が閾値<math>V_{th}</math> | と表すことができる。これに加え、膜電位が閾値<math>V_{th}</math>に到達した場合、その時刻に活動電位が発生したとみなし、膜電位をリセット電位<math>V_{reset}</math>にリセットするという処理を必要とする ('''図1A''')。従って、リーク電流を考慮したLeaky Integrate and Fireモデルは、 | ||
::<math> | ::<math> | ||
| 62行目: | 60行目: | ||
===非線形積分発火モデル=== | ===非線形積分発火モデル=== | ||
積分発火モデルは、 | |||
::<math>C_m\frac{dV}{dt}=F(V)+I_{ext}\mbox{ }\cdots( | ::<math>C_m\frac{dV}{dt}=F(V)+I_{ext}\mbox{ }\cdots(1)</math> | ||
::<math>F(V)=-G_L(V-E_L)\mbox{ }\cdots( | ::<math>F(V)=-G_L(V-E_L)\mbox{ }\cdots(2)</math> | ||
という線形微分方程式<math>F(V)</math>が1次関数) | という線形微分方程式<math>F(V)</math>が1次関数) である。しかし、神経細胞は非線形システムであり、Hodgkin-Huxleyモデルも非線形微分方程式である。このため、<math>F(V)</math>を非線形関数で表したモデルがいくつか提案されてきた。また、Hodgkin-Huxleyモデルから、早いチャネル変数を膜電位<math>V</math>の関数に置き換え、遅いチャネル変数を定数に置き換える近似により、非線形積分発火モデルを導出できる<ref name=Abbott1990>'''Abbott, L.F. & Kepler, T.B. (1990).'''<br>Model neurons: from Hodgkin-Huxley to Hopfield." In Statistical mechanics of neural networks (pp. 5-18). Springer, Berlin, Heidelberg. | ||
[https://doi.org/10.1007/3540532676_37 PDF]</ref><ref name=Jolivet2004><pubmed>15277599</pubmed></ref>。 | [https://doi.org/10.1007/3540532676_37 PDF]</ref><ref name=Jolivet2004><pubmed>15277599</pubmed></ref>[4,5]。 | ||
1つ目の拡張は、<math>F(V)</math>を2次関数<math>F(V)=\tfrac{G_L}{2\Delta_r}(V-V_r)^2</math> | 1つ目の拡張は、<math>F(V)</math>を2次関数<math>F(V)=\tfrac{G_L}{2\Delta_r}(V-V_r)^2</math>に拡張したQuadratic Integrate and Fire (QIF) モデルである。このモデルはサドルノード分岐を示す力学系の分岐点近傍の標準系 (Normal form) として得られたものである<ref name=Ermentrout1996><pubmed>8697231</pubmed></ref>[6]。Quadratic Integrate and Fireモデルには限られたタイプの発火パターンしか再現できないという問題があった。そこで、IzhikevichはQuadratic Integrate and Fireモデルを2変数<math>(V,U)</math>の微分方程式に拡張した<ref name=Izhikevich2003><pubmed>18244602</pubmed><br>MATLABコードが著者の [https://www.izhikevich.org/publications/spikes.htm ホームページ]にある。</ref>[7]。 | ||
::<math>C_m\frac{dV}{dt}=0.04V^2+5V+140-U+I_{ext}\mbox{ }\cdots( | ::<math>C_m\frac{dV}{dt}=0.04V^2+5V+140-U+I_{ext}\mbox{ }\cdots(3)</math> | ||
::<math>\frac{dV}{dt}=a(bV-U)\mbox{ }\cdots( | ::<math>\frac{dV}{dt}=a(bV-U)\mbox{ }\cdots(4)</math> | ||
ここで、<math>a,b</math>はパラメータである。膜電位<math>V</math>が閾値<math>30 mV</math>に達すると、変数<math>V</math>は<math>c</math>に、変数<math>U</math>は<math>U+d</math>にリセットされる。このモデルは、多様な神経細胞<ref name=McCormick1985><pubmed>2999347</pubmed></ref> <ref name=Nowak2003><pubmed>12626627</pubmed></ref>]が持つ、さまざまな発火特性を再現できる。 | ここで、<math>a,b</math>はパラメータである。膜電位<math>V</math>が閾値<math>30 mV</math>に達すると、変数<math>V</math>は<math>c</math>に、変数<math>U</math>は<math>U+d</math>にリセットされる。このモデルは、多様な神経細胞<ref name=McCormick1985><pubmed>2999347</pubmed></ref> <ref name=Nowak2003><pubmed>12626627</pubmed></ref>[8,9]が持つ、さまざまな発火特性を再現できる。 | ||
2つ目の拡張は、リーク電流に加え、指数関数のスパイク生成電流を考慮に入れたExponential Integrate and Fire (EIF) モデルである<ref name=Fourcaud-Trocme2003><pubmed>14684865</pubmed></ref>。 | 2つ目の拡張は、リーク電流に加え、指数関数のスパイク生成電流を考慮に入れたExponential Integrate and Fire (EIF) モデルである<ref name=Fourcaud-Trocme2003><pubmed>14684865</pubmed></ref>[10]。 | ||
::<math>F(V)=-G_L(V-E_L)+G_L\Delta{exp}(\frac{V-V_r}{\Delta_r})\mbox{ }\cdots( | ::<math>F(V)=-G_L(V-E_L)+G_L\Delta{exp}(\frac{V-V_r}{\Delta_r})\mbox{ }\cdots(5)</math> | ||
ここで<math>\Delta_r</math>はスパイクの立ち上がりの度合いを表現するパラメータであり<math>\Delta_r</math>が小さいほどスパイクの立上がりは急峻になる。<math>\Delta_r\to 0</math>の極限でExponential Integrate and Fireは通常の積分発火モデルになる。Exponential Integrate and FireモデルもQuadratic Integrate and Fireモデルと同様、限られたタイプの発火パターンしか再現できない という問題があった。BretteとGerstner はExponential Integrate and Fireモデルを2変数<math>(V,U)</math>の微分方程式に拡張した<ref name=Brette2005><pubmed>16014787</pubmed></ref>。このモデルも、多様な神経細胞が持つ、さまざまな発火パターンを再現できる<ref name=Naud2008><pubmed>19011922</pubmed></ref>。 | ここで<math>\Delta_r</math>はスパイクの立ち上がりの度合いを表現するパラメータであり<math>\Delta_r</math>が小さいほどスパイクの立上がりは急峻になる。<math>\Delta_r\to 0</math>の極限でExponential Integrate and Fireは通常の積分発火モデルになる。Exponential Integrate and FireモデルもQuadratic Integrate and Fireモデルと同様、限られたタイプの発火パターンしか再現できない という問題があった。BretteとGerstner はExponential Integrate and Fireモデルを2変数<math>(V,U)</math>の微分方程式に拡張した<ref name=Brette2005><pubmed>16014787</pubmed></ref> [11]。このモデルも、多様な神経細胞が持つ、さまざまな発火パターンを再現できる<ref name=Naud2008><pubmed>19011922</pubmed></ref>[12]。 | ||
[[ファイル:Kitano 積分発火モデルFig2.png|サムネイル|450px|'''図2. 積分発火モデルとMulti-timescale Adaptive Thresholdモデルの矩形波電流に対する応答'''<br> | [[ファイル:Kitano 積分発火モデルFig2.png|サムネイル|450px|'''図2. 積分発火モデルとMulti-timescale Adaptive Thresholdモデルの矩形波電流に対する応答'''<br> | ||
| 89行目: | 87行目: | ||
===変動閾値モデル=== | ===変動閾値モデル=== | ||
積分発火モデルは、膜電位<math>V</math>が閾値<math>V_{th}</math>に達すると、スパイクを生成し、膜電位<math>V_{reset}</math>をリセットする。積分発火モデルでは閾値を定数としている。その一方で、実験データ<ref name=Azouz2000><pubmed>10859358</pubmed></ref> <ref name=Henze2001><pubmed>11483306</pubmed></ref>やHodgikin-Huxleyモデル<ref name=Platkiewicz2010><pubmed>20628619</pubmed></ref><ref name=Kobayashi2016><pubmed>27085337</pubmed></ref>では閾値が変動しているという報告がある。 | 積分発火モデルは、膜電位<math>V</math>が閾値<math>V_{th}</math>に達すると、スパイクを生成し、膜電位<math>V_{reset}</math>をリセットする。積分発火モデルでは閾値を定数としている。その一方で、実験データ<ref name=Azouz2000><pubmed>10859358</pubmed></ref> <ref name=Henze2001><pubmed>11483306</pubmed></ref>[13,14] やHodgikin-Huxleyモデル<ref name=Platkiewicz2010><pubmed>20628619</pubmed></ref><ref name=Kobayashi2016><pubmed>27085337</pubmed></ref>[15,16] では閾値が変動しているという報告がある。 | ||
以下、閾値の変動を取り入れたモデルを紹介する。 | 以下、閾値の変動を取り入れたモデルを紹介する。 | ||
まず、スパイクによって閾値が変動すると考えられる。閾値がスパイクによって変動するモデルとして、Multi-timescale Adaptive Threshold (MAT) モデル<ref name=Kobayashi2009><pubmed>19668702</pubmed>C および MATLABコードが著者の[http://www.hk.k.u-tokyo.ac.jp/r-koba/applications/pred_JP.html ホームページ]にある。</ref>を紹介する。Multi-timescale Adaptive Thresholdモデルの閾値<math>V_{th}(t)</math>は次の式で書ける。 | |||
::<math>V_{th}(t)=\omega+\sum_{j:t_j<t}H(t-t_j)\mbox{ }\cdots( | ::<math>V_{th}(t)=\omega+\sum_{j:t_j<t}H(t-t_j)\mbox{ }\cdots(6)</math> | ||
::<math>H(t)=\alpha_1+r^{-t/\tau_1}+\alpha_2+r^{-t/\tau_2}\mbox{ }\cdots( | ::<math>H(t)=\alpha_1+r^{-t/\tau_1}+\alpha_2+r^{-t/\tau_2}\mbox{ }\cdots(7)</math> | ||
ここで<math>t_j</math>は<math>j</math> | ここで<math>t_j</math>は<math>j</math>番目のスパイク時刻であり、(6)式の和は時刻<math>t</math>までに起きたすべてのスパイクについて取る。また、<math>\omega</math>, <math>\alpha_1</math>, <math>\alpha_2</math>はモデルパラメータ、<math>\tau_1=10\mbox{ }[ms]</math>, <math>\tau_2=200\mbox{ }[ms]</math>は時定数である。Multi-timescale Adaptive Thresholdモデルは、膜電位が閾値に達したら、膜電位をリセットする代わりに閾値を上昇させるという点において積分発火モデルと異なる('''図1''')。このモデルは、わずか3つのパラメータで脳を構成する多様な発火パターンを再現する ('''図2''')。Multi-timescale Adaptive Thresholdモデルは、スパイクに着目した線形化近似を行うことで、Hodgikin-Huxleyモデルから導出することもできる<ref name=Kobayashi2016></ref>[16]。この解析により、速い時定数<math>\thicksim 10\mbox{ }[ms]</math> は膜時定数、遅い時定数<math>\thicksim 200\mbox{ }[ms]</math>は遅いカリウムイオン電流 (Mタイプ電流K<sup>+</sup>電流やCa<sup>2+</sup>活性化K<sup>+</sup>電流) に対応することが示された<ref name=Kobayashi2016></ref>[16]。また、Multi-timescale Adaptive Thresholdモデルではカーネル<math>H(t)</math>として2つの指数関数の和を仮定したが、<math>H(t)</math>として指数関数を仮定し、膜電位をリセットするモデルもある<ref name=Liu2001><pubmed>11316338</pubmed></ref><ref name=Jolivet2008><pubmed>18160135</pubmed></ref><ref name=Levakova2019><pubmed>31387478</pubmed></ref> [18,19,20]。 | ||
また、閾値は膜電位<math>V</math>やその微分<math>\tfrac{dv}{dt}</math>によって変動すると考えられる。Azouz とGray は''in vivo''膜電位データを分析し、閾値が膜電位の微分に依存することを示した<ref name=Azouz2000><pubmed>10859358</pubmed></ref>。また、膜電位の微分情報を活用することによって、Hodgikin-Huxleyモデルに対するスパイクの予測精度が向上することが示されている<ref name=Kobayashi2007><pubmed>17358202</pubmed></ref>。この結果は、Hodgikin-Huxleyモデルの閾値が膜電位の微分に依存することを示唆している。PlatkiewiczとBretteは、Hodgikin-Huxleyモデルの閾値は近似的に以下の式に従うことを示した<ref name=Platkiewicz2010><pubmed>20628619</pubmed></ref>。 | また、閾値は膜電位<math>V</math>やその微分<math>\tfrac{dv}{dt}</math>によって変動すると考えられる。Azouz とGray は''in vivo''膜電位データを分析し、閾値が膜電位の微分に依存することを示した<ref name=Azouz2000><pubmed>10859358</pubmed></ref>[13]。また、膜電位の微分情報を活用することによって、Hodgikin-Huxleyモデルに対するスパイクの予測精度が向上することが示されている<ref name=Kobayashi2007><pubmed>17358202</pubmed></ref>[21]。この結果は、Hodgikin-Huxleyモデルの閾値が膜電位の微分に依存することを示唆している。PlatkiewiczとBretteは、Hodgikin-Huxleyモデルの閾値は近似的に以下の式に従うことを示した<ref name=Platkiewicz2010><pubmed>20628619</pubmed></ref>[15]。 | ||
::<math>V_{th}(t)\thickapprox V_T-k_a\log{h}\mbox{ }\cdots( | ::<math>V_{th}(t)\thickapprox V_T-k_a\log{h}\mbox{ }\cdots(8)</math> | ||
<math>h</math>はNaチャネルのゲート変数、<math>k_a</math>, <math>V_T</math>は定数である。式( | <math>h</math>はNaチャネルのゲート変数、<math>k_a</math>, <math>V_T</math>は定数である。式(8)は、実験データやHodgikin-Huxleyモデルで観察された、閾値が膜電位の微分に依存する性質を説明できる。 | ||
スパイクと膜電位のどちらの影響も考慮に入れたモデルもある。山内らは、閾値の膜電位依存性を考慮に入れたMulti-timescale Adaptive Thresholdモデルを提案した<ref name=Yamauchi2011><pubmed>22203798</pubmed></ref>。 | スパイクと膜電位のどちらの影響も考慮に入れたモデルもある。山内らは、閾値の膜電位依存性を考慮に入れたMulti-timescale Adaptive Thresholdモデルを提案した<ref name=Yamauchi2011><pubmed>22203798</pubmed></ref>[22]。 | ||
::<math>V_{th}(t)=\omega+\sum_{j:t_j<t}H(t-t_j)+\beta\int\alpha(s)\frac{dV}{dT}(t-s)dS\mbox{ }\cdots( | ::<math>V_{th}(t)=\omega+\sum_{j:t_j<t}H(t-t_j)+\beta\int\alpha(s)\frac{dV}{dT}(t-s)dS\mbox{ }\cdots(9)</math> | ||
ここで<math>H(t)</math>は式( | ここで<math>H(t)</math>は式(7)で定義されるカーネル、<math>\alpha(S)=se^{-s/\tau V}\mbox{ }(\tau_V=5\mbox{ }[ms]</math>)はアルファ関数である。このモデルは4つのモデルパラメーター<math>\omega</math>, <math>\alpha_1</math>, <math>\alpha_2</math>, <math>\beta</math>を持つ。このモデルは、実験データのスパイクを高精度に予測でき、かつ、Izhikevichモデルと同様に多様な神経細胞が持つ、さまざまな発火パターンを再現できる<ref name=Yamauchi2011></ref> [22]。 | ||
===Spike Response Model=== | ===Spike Response Model=== | ||
変動電流<math>I(t)</math>が積分発火モデルに注入されている状況を考えよう。ニューロンは時刻<math>0</math>に発火し、その後時刻<math>t</math>まで発火しないとすると、膜電位は | 変動電流<math>I(t)</math>が積分発火モデルに注入されている状況を考えよう。ニューロンは時刻<math>0</math>に発火し、その後時刻<math>t</math>まで発火しないとすると、膜電位は | ||
::<math>V(t)=V_{reset}e^{-t/\tau{_m}}+\int_0^t I(t-s)e^{-s/\tau{_m}}ds\mbox{ }\cdots( | ::<math>V(t)=V_{reset}e^{-t/\tau{_m}}+\int_0^t I(t-s)e^{-s/\tau{_m}}ds\mbox{ }\cdots(10)</math> | ||
と書ける。表記を単純にするため、<math>E_L=0</math>とした。式( | と書ける。表記を単純にするため、<math>E_L=0</math>とした。式(10) を以下のように拡張したモデルはSpike Response Model (SRM) と呼ばれている<ref name=Gerstner2002>'''Gerstner, W. & Kistler, W.M. (2002).'''<br>Spiking neuron models: Single neurons, populations, plasticity., Cambridge: Cambridge University Press. [https://doi.org/10.1017/CBO9780511815706 PDF] </ref> [23] 。 | ||
::<math>V(t)=\eta(t)+\int_0^t \kappa(s)I(t-s)ds\mbox{ }\cdots(11)</math> | ::<math>V(t)=\eta(t)+\int_0^t \kappa(s)I(t-s)ds\mbox{ }\cdots(11)</math> | ||
<math>\eta(t)</math>, <math>\kappa(s)</math>はカーネルと呼ばれる関数である。カーネルがどちらも同じ時定数の指数関数であれば積分発火モデルとなる。Spike Response Modelは Hodgikin-Huxleyモデルで観察されている共鳴特性 (特定の周波数の入力に発火しやすい性質) | <math>\eta(t)</math>, <math>\kappa(s)</math>はカーネルと呼ばれる関数である。カーネルがどちらも同じ時定数の指数関数であれば積分発火モデルとなる。Spike Response Modelは Hodgikin-Huxleyモデルで観察されている共鳴特性 (特定の周波数の入力に発火しやすい性質) を再現できる。共鳴特性を再現するモデルとしてResonate-and-Fireモデル <ref name=Izhikevich2001><pubmed>11665779</pubmed></ref>[24] がよく知られているが、このモデルもSpike Response Modelの特殊な場合となる。 | ||
==神経細胞モデル間の比較== | ==神経細胞モデル間の比較== | ||
これまで、積分発火モデルとその様々な拡張モデルについて紹介を行った。本節では、4つの神経細胞モデル ( | これまで、積分発火モデルとその様々な拡張モデルについて紹介を行った。本節では、4つの神経細胞モデル (積分発火モデル、Izhikevichモデル、Multi-timescale Adaptive Thresholdモデル、Hodgikin-Huxleyモデル) について比較を行い、モデルの特徴を整理する('''表''')。 | ||
まず、モデルの再現性、つまり、数理モデルが実際の神経細胞の発火パターンを再現できるかどうかについて考えよう。モデルの再現性として、 | まず、モデルの再現性、つまり、数理モデルが実際の神経細胞の発火パターンを再現できるかどうかについて考えよう。モデルの再現性として、 | ||
| 130行目: | 128行目: | ||
* 実験データを正確に予測できる (定量的再現性) | * 実験データを正確に予測できる (定量的再現性) | ||
の2つがある。積分発火モデルは、単純化されすぎているため、限られたタイプ ( | の2つがある。積分発火モデルは、単純化されすぎているため、限られたタイプ (Fast Spiking細胞) の発火パターンしか再現できない。Izhikevichモデル、Multi-timescale Adaptive Thresholdモデルは、多様な神経細胞のさまざまな発火パターンを定性的に再現できる。Multi-timescale Adaptive Thresholdモデルはスパイク予測の国際コンペで優勝するなど実験データを高精度に予測できる<ref name=Kobayashi2009></ref><ref name=Gerstner2009><pubmed>19833951</pubmed></ref> [17,25] 。Izhikevichモデルは分岐点近傍のモデルであるため、定量的予測には不向きである<ref name=Rossant2011><pubmed>21415925</pubmed></ref> [26]。Hodgikin-Huxleyモデルは、さまざまな発火パターンを定性的に再現できるものの、異なる細胞タイプをシミュレーションするにはイオン電流を調整する必要がある。この調整には専門知識と経験を必要とする。また、個別の実験データにフィットしたり予測したりすることは困難であることが多い。 | ||
次に、これらのモデルを脳のシミュレーション (数値計算) に使うことを考えよう。 | 次に、これらのモデルを脳のシミュレーション (数値計算) に使うことを考えよう。 | ||
大規模な神経回路をシミュレーションするためには、高速かつ正確に数値計算できることが望ましい。積分発火モデルとMulti-timescale Adaptive Thresholdモデルは、膜電位と閾値を解析的に計算できるため<ref name=Yamauchi2011><pubmed>22203798</pubmed></ref>、刻み幅や数値誤差の問題に悩むことなくシミュレーションを実行できる。Izhikevichモデルは Hodgikin-Huxleyモデルに比べると非線形性が弱いので高速に計算できるが、膜電位を解析的に計算できないため、刻み幅や数値誤差に注意をしつつシミュレーションを行う必要がある。 | 大規模な神経回路をシミュレーションするためには、高速かつ正確に数値計算できることが望ましい。積分発火モデルとMulti-timescale Adaptive Thresholdモデルは、膜電位と閾値を解析的に計算できるため<ref name=Yamauchi2011><pubmed>22203798</pubmed></ref>[22]、刻み幅や数値誤差の問題に悩むことなくシミュレーションを実行できる。Izhikevichモデルは Hodgikin-Huxleyモデルに比べると非線形性が弱いので高速に計算できるが、膜電位を解析的に計算できないため、刻み幅や数値誤差に注意をしつつシミュレーションを行う必要がある。 | ||
また、神経回路の理論的解析を行うためにはモデルがシンプルなことが望ましい。そのため、理論研究では積分発火モデルが使われることが多い。Multi-timescale Adaptive Thresholdモデルの閾値変動は複雑であるものの、方程式自体は線形なのでそれほど困難ではないと予想される。IzhikevichモデルとHodgikin-Huxleyモデルは非線形微分方程式であるため、解析は困難である。 | また、神経回路の理論的解析を行うためにはモデルがシンプルなことが望ましい。そのため、理論研究では積分発火モデルが使われることが多い。Multi-timescale Adaptive Thresholdモデルの閾値変動は複雑であるものの、方程式自体は線形なのでそれほど困難ではないと予想される。IzhikevichモデルとHodgikin-Huxleyモデルは非線形微分方程式であるため、解析は困難である。 | ||
最後に、モデルパラメータの解釈性について考えよう。Hodgikin-Huxleyモデルは、全てのパラメータがイオンチャネルと対応しているため、パラメータの解釈を行うことが容易である。その一方、積分発火モデルやIzhikevichモデルは単純化されすぎているため、パラメータの生理学的意味を解釈することはできない。このため、積分発火モデルやその拡張モデルは現象論的モデルと呼ばれることもある。Multi-timescale Adaptive | 最後に、モデルパラメータの解釈性について考えよう。Hodgikin-Huxleyモデルは、全てのパラメータがイオンチャネルと対応しているため、パラメータの解釈を行うことが容易である。その一方、積分発火モデルやIzhikevichモデルは単純化されすぎているため、パラメータの生理学的意味を解釈することはできない。このため、積分発火モデルやその拡張モデルは現象論的モデルと呼ばれることもある。Multi-timescale Adaptive Thresholdモデルのパラメータは、複数のイオン電流の効果が合わさったものに対応している。このため、パラメータから遅いカリウム電流の有無などを解釈できるものの、イオン電流の詳細については解釈できない。 | ||
{| class="wikitable" style="text-align: center | {| class="wikitable" style="text-align: center | ||
2021年10月2日 (土) 14:18時点における版
小林 亮太
東京大学大学院 新領域創成科学研究科
北野 勝則
立命館大学 情報理工学部
DOI:10.14931/bsd.9934 原稿受付日:2021年7月26日 原稿完成日:2021年10月2日
担当編集委員:五味 裕章(NTTコミュニケーション科学基礎研究所 人間情報研究部)
積分発火モデルは、神経細胞の電気活動を数理的に記述するモデルの1つである。神経細胞の電気的状態を膜電位により表し、神経細胞の出力である活動電位 (スパイク) の生成過程の記述を省略し、活動電位の閾値以下の範囲における膜電位の変化を微分方程式により記述する。活動電位の生成機構もモデル化するHodgkin-Huxleyモデルよりも計算コストが少ないため、膜電位変化を記述する神経細胞モデルとして、広く用いられている。
はじめに
神経細胞の電気的特性については、HodgkinとHuxleyによって細胞膜上に発現しているイオンチャネルの膜電位依存性とそれらによる活動電位生成機構、およびその数理的な表現が明らかにされたが[1][1]、それ以前にLapicqueによって、細胞膜のキャパシタとしての特性や神経興奮現象(活動電位生成)に対する閾値となる電位、および、閾値に到るまでの過程について詳細に調べられていた[2][3] [2,3]。入力として与えられた電流はキャパシタとしての特性により膜電位に積算(integrate)される。膜電位が上昇して閾値に到達すると、活動電位を発生(fire)する。この膜電位の閾値に達するまでの積算過程をモデル化したのが、積分発火モデルである。このモデルでは活動電位生成中の膜電位変動は記述しない。それは非常に短時間(< 2msec)の過程であり、膜電位挙動のほとんどの時間が閾値に到るまでの積算過程であるとみなせるためである。神経細胞の状態を表す変数が膜電位のみの1変数であるため、計算量も多くない。このため、多くの研究において、採用されてきたモデルである。一方で、神経細胞応答の本質であるアクティブな膜伝導性を一切無視したモデルであるため、実際の神経細胞応答とは異なる特性を示すことから、その拡張モデルも多く提案されてきた。以下では、まず、基本となる積分発火モデルであるLeaky Integrate-and-Fireモデル(LIFモデル、と呼ばれる)を解説し、次にその拡張モデルとして代表的なものを紹介する。
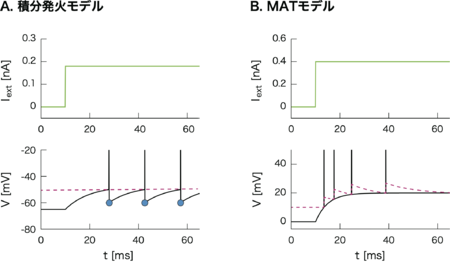
A. 積分発火モデル:スパイクを生成すると、膜電位をリセット電位構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle V_{reset}} (シアン) にリセットする。パラメータは構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \tau_m=10\mbox{ }[ms]} , 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle R_m=10\mbox{ }[M\Omega]} , 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle E_L=-65\mbox{ }[mV]} , 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle V_{th}= -50\mbox{ }[mV]} , 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle V_{rest}= -60\mbox{ }[mV]} である。
B. Multi-timescale Adaptive Thresholdモデル:スパイクを生成すると、膜電位をリセットせずに閾値 (マゼンタ) を変動させる。閾値パラメータは, , 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \alpha_2=3\mbox{ }[mV]} である。その他 のパラメータは構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \tau_m=5\mbox{ }[ms]} , 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle R_m=10\mbox{ }[M\Omega]} , である。
積分発火モデル
Integrate and fire model
脂質二重層からなる神経細胞の細胞膜により、電荷をもつイオンは細胞膜からの流出入を妨げてられている。細胞外の電位を基準電位 (0 mV) とした場合、細胞内の電位を表す膜電位は、通常、負の値をもつ過分極した状態(およそ–70 mV付近)をとる。神経細胞は、細胞膜の外側と内側にそれぞれ正の電荷および負の電荷をもつイオンを帯電させた状態になり、細胞膜はキャパシタの性質を有する。細胞膜上に発現したタンパク質であるイオンチャネルが、その状態によってイオンの流出入を促す場合があり、膜電位の変化をもたらす。膜電位をとし、細胞膜の膜容量を、細胞膜(実際にはイオンチャンネル)を透過する電流 (膜電流) をとすると、
と表せる(膜電流は慣習として、外向きを正にとる)。膜電位変化に寄与する電流として、外部からの注入電流を考慮すると、
のように書ける。
膜電流は、細胞膜上に発現するイオンチャネルを透過する電流を表す。イオンチャネルは、典型的には10種類程度発現し、それぞれ異なる特性を有する。各イオンチャネルを透過する電流のコンダクタンス(あるいは、その逆数の抵抗)は、膜電位に依存して変化するアクティブな性質をもち、この性質によりパルス状の膜電位変化である活動電位が生成される。しかし、活動電位は、膜電位が閾値と呼ばれるレベルまで上昇すると、そこからさらに急速に上昇して正の電位に到達後、急速に下降して閾値以下の過分極したレベルまで戻る(リセットと呼ぶ)という定型の変化を示すことから、活動電位生成中の変化は省略し、リセット後から閾値到達までの変化のみを定式化する。膜電流としては、アクティブな伝導性を無視し、伝導性の時間に不変な成分を括り出したリーク電流のみを採用する。リーク電流は、時間に不変なコンダクタンスを、この電流の反転電位をとすると、
と表すことができる。これに加え、膜電位が閾値に到達した場合、その時刻に活動電位が発生したとみなし、膜電位をリセット電位にリセットするという処理を必要とする (図1A)。従って、リーク電流を考慮したLeaky Integrate and Fireモデルは、
と表せる。閾値以下の範囲では、膜電位の変化は微分方程式(1)に従う。
(1)式の両辺をで割ることにより、, を用いて
を得る。構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \tau_m} 、構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle R_m} はそれぞれ、膜時定数、膜抵抗と呼ばれる。
このように、積分発火モデルにおける膜電位の変化は、線形の微分方程式で表される。従って、膜電位の挙動は解析的に計算できることが可能であり、神経細胞や神経回路の挙動に関する理論的解析が行いやすく、多くの研究で用いられてきた。
拡張された積分発火モデル
積分発火モデルは、単純化されすぎているため、神経細胞のスパイク応答のパターンを正確に再現できない、という問題がある。この問題を解決するため、積分発火モデルのさまざまな拡張が考えられてきた。以下、3つのタイプの拡張モデルを説明する。
非線形積分発火モデル
積分発火モデルは、
という線形微分方程式が1次関数) である。しかし、神経細胞は非線形システムであり、Hodgkin-Huxleyモデルも非線形微分方程式である。このため、構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle F(V)} を非線形関数で表したモデルがいくつか提案されてきた。また、Hodgkin-Huxleyモデルから、早いチャネル変数を膜電位構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle V} の関数に置き換え、遅いチャネル変数を定数に置き換える近似により、非線形積分発火モデルを導出できる[4][5][4,5]。
1つ目の拡張は、構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle F(V)} を2次関数構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle F(V)=\tfrac{G_L}{2\Delta_r}(V-V_r)^2} に拡張したQuadratic Integrate and Fire (QIF) モデルである。このモデルはサドルノード分岐を示す力学系の分岐点近傍の標準系 (Normal form) として得られたものである[6][6]。Quadratic Integrate and Fireモデルには限られたタイプの発火パターンしか再現できないという問題があった。そこで、IzhikevichはQuadratic Integrate and Fireモデルを2変数構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle (V,U)} の微分方程式に拡張した[7][7]。
- 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle C_m\frac{dV}{dt}=0.04V^2+5V+140-U+I_{ext}\mbox{ }\cdots(3)}
- 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \frac{dV}{dt}=a(bV-U)\mbox{ }\cdots(4)}
ここで、構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle a,b} はパラメータである。膜電位構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle V} が閾値構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle 30 mV} に達すると、変数構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle V} は構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle c} に、変数構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle U} は構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle U+d} にリセットされる。このモデルは、多様な神経細胞[8] [9][8,9]が持つ、さまざまな発火特性を再現できる。
2つ目の拡張は、リーク電流に加え、指数関数のスパイク生成電流を考慮に入れたExponential Integrate and Fire (EIF) モデルである[10][10]。
- 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle F(V)=-G_L(V-E_L)+G_L\Delta{exp}(\frac{V-V_r}{\Delta_r})\mbox{ }\cdots(5)}
ここではスパイクの立ち上がりの度合いを表現するパラメータでありが小さいほどスパイクの立上がりは急峻になる。の極限でExponential Integrate and Fireは通常の積分発火モデルになる。Exponential Integrate and FireモデルもQuadratic Integrate and Fireモデルと同様、限られたタイプの発火パターンしか再現できない という問題があった。BretteとGerstner はExponential Integrate and Fireモデルを2変数の微分方程式に拡張した[11] [11]。このモデルも、多様な神経細胞が持つ、さまざまな発火パターンを再現できる[12][12]。
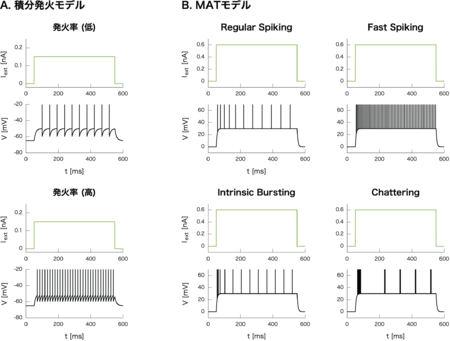
ある矩形波電流に対して、2つの神経細胞モデルが示す発火パターンを示した。
A. 積分発火モデル: 発火率の異なる神経細胞を再現できる。パラメータは、(上), (下)、電流の強さはである。
B. Multi-timescale Adaptive Thresholdモデル: 神経細胞の多様な発火パターンを再現できる。Chattering 細胞はたくさんスパイクを出した後、2 回ずつスパイクを出している。閾値パラメータは、, 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \alpha_1=25\mbox{ }[mV]} , 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \alpha_2=2\mbox{ }[mV]} (Regular Spiking), 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \omega=20\mbox{ }[mV]} , 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \alpha_1=2\mbox{ }[mV]} , 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \alpha_2=3\mbox{ }[mV]} (Intrinsic Spiking), 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \omega=20\mbox{ }[mV]} , 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \alpha_1=10\mbox{ }[mV]} , 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \alpha_2=0.2\mbox{ }[mV]} (Fast Spiking), 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \omega=28\mbox{ }[mV]} , 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \alpha_1=-0.52\mbox{ }[mV]} , 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \alpha_2=0.4\mbox{ }[mV]} (Chattering)、電流の強さは構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle I_0=0.6\mbox{ }[nA]} である。
変動閾値モデル
積分発火モデルは、膜電位構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle V} が閾値構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle V_{th}} に達すると、スパイクを生成し、膜電位構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle V_{reset}} をリセットする。積分発火モデルでは閾値を定数としている。その一方で、実験データ[13] [14][13,14] やHodgikin-Huxleyモデル[15][16][15,16] では閾値が変動しているという報告がある。
以下、閾値の変動を取り入れたモデルを紹介する。
まず、スパイクによって閾値が変動すると考えられる。閾値がスパイクによって変動するモデルとして、Multi-timescale Adaptive Threshold (MAT) モデル[17]を紹介する。Multi-timescale Adaptive Thresholdモデルの閾値構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle V_{th}(t)} は次の式で書ける。
- 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle V_{th}(t)=\omega+\sum_{j:t_j<t}H(t-t_j)\mbox{ }\cdots(6)}
- 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle H(t)=\alpha_1+r^{-t/\tau_1}+\alpha_2+r^{-t/\tau_2}\mbox{ }\cdots(7)}
ここで構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle t_j} は構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle j} 番目のスパイク時刻であり、(6)式の和は時刻構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle t} までに起きたすべてのスパイクについて取る。また、構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \omega} , 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \alpha_1} , 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \alpha_2} はモデルパラメータ、構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \tau_1=10\mbox{ }[ms]} , 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \tau_2=200\mbox{ }[ms]} は時定数である。Multi-timescale Adaptive Thresholdモデルは、膜電位が閾値に達したら、膜電位をリセットする代わりに閾値を上昇させるという点において積分発火モデルと異なる(図1)。このモデルは、わずか3つのパラメータで脳を構成する多様な発火パターンを再現する (図2)。Multi-timescale Adaptive Thresholdモデルは、スパイクに着目した線形化近似を行うことで、Hodgikin-Huxleyモデルから導出することもできる[16][16]。この解析により、速い時定数構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \thicksim 10\mbox{ }[ms]} は膜時定数、遅い時定数構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \thicksim 200\mbox{ }[ms]} は遅いカリウムイオン電流 (Mタイプ電流K+電流やCa2+活性化K+電流) に対応することが示された[16][16]。また、Multi-timescale Adaptive Thresholdモデルではカーネル構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle H(t)} として2つの指数関数の和を仮定したが、構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle H(t)} として指数関数を仮定し、膜電位をリセットするモデルもある[18][19][20] [18,19,20]。
また、閾値は膜電位構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle V} やその微分構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \tfrac{dv}{dt}} によって変動すると考えられる。Azouz とGray はin vivo膜電位データを分析し、閾値が膜電位の微分に依存することを示した[13][13]。また、膜電位の微分情報を活用することによって、Hodgikin-Huxleyモデルに対するスパイクの予測精度が向上することが示されている[21][21]。この結果は、Hodgikin-Huxleyモデルの閾値が膜電位の微分に依存することを示唆している。PlatkiewiczとBretteは、Hodgikin-Huxleyモデルの閾値は近似的に以下の式に従うことを示した[15][15]。
- 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle V_{th}(t)\thickapprox V_T-k_a\log{h}\mbox{ }\cdots(8)}
構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle h} はNaチャネルのゲート変数、構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle k_a} , 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle V_T} は定数である。式(8)は、実験データやHodgikin-Huxleyモデルで観察された、閾値が膜電位の微分に依存する性質を説明できる。
スパイクと膜電位のどちらの影響も考慮に入れたモデルもある。山内らは、閾値の膜電位依存性を考慮に入れたMulti-timescale Adaptive Thresholdモデルを提案した[22][22]。
- 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle V_{th}(t)=\omega+\sum_{j:t_j<t}H(t-t_j)+\beta\int\alpha(s)\frac{dV}{dT}(t-s)dS\mbox{ }\cdots(9)}
ここで構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle H(t)} は式(7)で定義されるカーネル、構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \alpha(S)=se^{-s/\tau V}\mbox{ }(\tau_V=5\mbox{ }[ms]} )はアルファ関数である。このモデルは4つのモデルパラメーター構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \omega} , 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \alpha_1} , 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \alpha_2} , 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \beta} を持つ。このモデルは、実験データのスパイクを高精度に予測でき、かつ、Izhikevichモデルと同様に多様な神経細胞が持つ、さまざまな発火パターンを再現できる[22] [22]。
Spike Response Model
変動電流構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle I(t)} が積分発火モデルに注入されている状況を考えよう。ニューロンは時刻構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle 0} に発火し、その後時刻構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle t} まで発火しないとすると、膜電位は
- 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle V(t)=V_{reset}e^{-t/\tau{_m}}+\int_0^t I(t-s)e^{-s/\tau{_m}}ds\mbox{ }\cdots(10)}
と書ける。表記を単純にするため、構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle E_L=0} とした。式(10) を以下のように拡張したモデルはSpike Response Model (SRM) と呼ばれている[23] [23] 。
- 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle V(t)=\eta(t)+\int_0^t \kappa(s)I(t-s)ds\mbox{ }\cdots(11)}
構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \eta(t)} , 構文解析に失敗 (SVG (ブラウザーのプラグインで MathML を有効にできます): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \kappa(s)} はカーネルと呼ばれる関数である。カーネルがどちらも同じ時定数の指数関数であれば積分発火モデルとなる。Spike Response Modelは Hodgikin-Huxleyモデルで観察されている共鳴特性 (特定の周波数の入力に発火しやすい性質) を再現できる。共鳴特性を再現するモデルとしてResonate-and-Fireモデル [24][24] がよく知られているが、このモデルもSpike Response Modelの特殊な場合となる。
神経細胞モデル間の比較
これまで、積分発火モデルとその様々な拡張モデルについて紹介を行った。本節では、4つの神経細胞モデル (積分発火モデル、Izhikevichモデル、Multi-timescale Adaptive Thresholdモデル、Hodgikin-Huxleyモデル) について比較を行い、モデルの特徴を整理する(表)。
まず、モデルの再現性、つまり、数理モデルが実際の神経細胞の発火パターンを再現できるかどうかについて考えよう。モデルの再現性として、
- 似たような挙動を再現できる (定性的再現性)、
- 実験データを正確に予測できる (定量的再現性)
の2つがある。積分発火モデルは、単純化されすぎているため、限られたタイプ (Fast Spiking細胞) の発火パターンしか再現できない。Izhikevichモデル、Multi-timescale Adaptive Thresholdモデルは、多様な神経細胞のさまざまな発火パターンを定性的に再現できる。Multi-timescale Adaptive Thresholdモデルはスパイク予測の国際コンペで優勝するなど実験データを高精度に予測できる[17][25] [17,25] 。Izhikevichモデルは分岐点近傍のモデルであるため、定量的予測には不向きである[26] [26]。Hodgikin-Huxleyモデルは、さまざまな発火パターンを定性的に再現できるものの、異なる細胞タイプをシミュレーションするにはイオン電流を調整する必要がある。この調整には専門知識と経験を必要とする。また、個別の実験データにフィットしたり予測したりすることは困難であることが多い。
次に、これらのモデルを脳のシミュレーション (数値計算) に使うことを考えよう。
大規模な神経回路をシミュレーションするためには、高速かつ正確に数値計算できることが望ましい。積分発火モデルとMulti-timescale Adaptive Thresholdモデルは、膜電位と閾値を解析的に計算できるため[22][22]、刻み幅や数値誤差の問題に悩むことなくシミュレーションを実行できる。Izhikevichモデルは Hodgikin-Huxleyモデルに比べると非線形性が弱いので高速に計算できるが、膜電位を解析的に計算できないため、刻み幅や数値誤差に注意をしつつシミュレーションを行う必要がある。
また、神経回路の理論的解析を行うためにはモデルがシンプルなことが望ましい。そのため、理論研究では積分発火モデルが使われることが多い。Multi-timescale Adaptive Thresholdモデルの閾値変動は複雑であるものの、方程式自体は線形なのでそれほど困難ではないと予想される。IzhikevichモデルとHodgikin-Huxleyモデルは非線形微分方程式であるため、解析は困難である。
最後に、モデルパラメータの解釈性について考えよう。Hodgikin-Huxleyモデルは、全てのパラメータがイオンチャネルと対応しているため、パラメータの解釈を行うことが容易である。その一方、積分発火モデルやIzhikevichモデルは単純化されすぎているため、パラメータの生理学的意味を解釈することはできない。このため、積分発火モデルやその拡張モデルは現象論的モデルと呼ばれることもある。Multi-timescale Adaptive Thresholdモデルのパラメータは、複数のイオン電流の効果が合わさったものに対応している。このため、パラメータから遅いカリウム電流の有無などを解釈できるものの、イオン電流の詳細については解釈できない。
| 積分発火モデル | Izhikevich モデル | Multi-timescale Adaptive Thresholdモデル | Hodgikin-Huxleyモデル | |
|---|---|---|---|---|
| 定性的な再現性 | ✖️ | ○ | ○ | △ |
| 定量的な再現性:予測精度 | ✖️ | ✖️ | ○ | ✖️ |
| 数値計算の速さ:計算速度 | ○ | △ | ○ | ✖️ |
| 数値計算の精度:数値誤差 | ○ | ✖️ | ○ | ✖️ |
| 理論的な取り扱いの容易さ | ○ | ✖️ | △ | ✖️ |
| パラメータの解釈性 | ✖️ | ✖️ | △ | ○ |
○:適したモデルである、△:最適なモデルとは言えない、✖️:目的に合わない。
関連項目
参考文献
- ↑
HODGKIN, A.L., & HUXLEY, A.F. (1952).
A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of physiology, 117(4), 500-44. [PubMed:12991237] [PMC] [WorldCat] [DOI] - ↑ Lapicque, L. (1907).
Recherches quantitatives sur l'excitation électrique des nerfs traitée comme une polarization. Journal de physiologie et de pathologie générale, 9, 620-635. - ↑
Lapicque, L. (2007).
Quantitative investigations of electrical nerve excitation treated as polarization. 1907. Biological cybernetics, 97(5-6), 341-9. [PubMed:18046573] [WorldCat] [DOI] - ↑ Abbott, L.F. & Kepler, T.B. (1990).
Model neurons: from Hodgkin-Huxley to Hopfield." In Statistical mechanics of neural networks (pp. 5-18). Springer, Berlin, Heidelberg. PDF - ↑
Jolivet, R., Lewis, T.J., & Gerstner, W. (2004).
Generalized integrate-and-fire models of neuronal activity approximate spike trains of a detailed model to a high degree of accuracy. Journal of neurophysiology, 92(2), 959-76. [PubMed:15277599] [WorldCat] [DOI] - ↑
Ermentrout, B. (1996).
Type I membranes, phase resetting curves, and synchrony. Neural computation, 8(5), 979-1001. [PubMed:8697231] [WorldCat] [DOI] - ↑
Izhikevich, E.M. (2003).
Simple model of spiking neurons. IEEE transactions on neural networks, 14(6), 1569-72. [PubMed:18244602] [WorldCat] [DOI]
MATLABコードが著者の ホームページにある。 - ↑
McCormick, D.A., Connors, B.W., Lighthall, J.W., & Prince, D.A. (1985).
Comparative electrophysiology of pyramidal and sparsely spiny stellate neurons of the neocortex. Journal of neurophysiology, 54(4), 782-806. [PubMed:2999347] [WorldCat] [DOI] - ↑
Nowak, L.G., Azouz, R., Sanchez-Vives, M.V., Gray, C.M., & McCormick, D.A. (2003).
Electrophysiological classes of cat primary visual cortical neurons in vivo as revealed by quantitative analyses. Journal of neurophysiology, 89(3), 1541-66. [PubMed:12626627] [WorldCat] [DOI] - ↑
Fourcaud-Trocmé, N., Hansel, D., van Vreeswijk, C., & Brunel, N. (2003).
How spike generation mechanisms determine the neuronal response to fluctuating inputs. The Journal of neuroscience : the official journal of the Society for Neuroscience, 23(37), 11628-40. [PubMed:14684865] [PMC] [WorldCat] - ↑
Brette, R., & Gerstner, W. (2005).
Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. Journal of neurophysiology, 94(5), 3637-42. [PubMed:16014787] [WorldCat] [DOI] - ↑
Naud, R., Marcille, N., Clopath, C., & Gerstner, W. (2008).
Firing patterns in the adaptive exponential integrate-and-fire model. Biological cybernetics, 99(4-5), 335-47. [PubMed:19011922] [PMC] [WorldCat] [DOI] - ↑ 13.0 13.1
Azouz, R., & Gray, C.M. (2000).
Dynamic spike threshold reveals a mechanism for synaptic coincidence detection in cortical neurons in vivo. Proceedings of the National Academy of Sciences of the United States of America, 97(14), 8110-5. [PubMed:10859358] [PMC] [WorldCat] [DOI] - ↑
Henze, D.A., & Buzsáki, G. (2001).
Action potential threshold of hippocampal pyramidal cells in vivo is increased by recent spiking activity. Neuroscience, 105(1), 121-30. [PubMed:11483306] [WorldCat] [DOI] - ↑ 15.0 15.1
Platkiewicz, J., & Brette, R. (2010).
A threshold equation for action potential initiation. PLoS computational biology, 6(7), e1000850. [PubMed:20628619] [PMC] [WorldCat] [DOI] - ↑ 16.0 16.1 16.2
Kobayashi, R., & Kitano, K. (2016).
Impact of slow K(+) currents on spike generation can be described by an adaptive threshold model. Journal of computational neuroscience, 40(3), 347-62. [PubMed:27085337] [PMC] [WorldCat] [DOI] - ↑ 17.0 17.1
Kobayashi, R., Tsubo, Y., & Shinomoto, S. (2009).
Made-to-order spiking neuron model equipped with a multi-timescale adaptive threshold. Frontiers in computational neuroscience, 3, 9. [PubMed:19668702] [PMC] [WorldCat] [DOI] C および MATLABコードが著者のホームページにある。 - ↑
Liu, Y.H., & Wang, X.J. (2001).
Spike-frequency adaptation of a generalized leaky integrate-and-fire model neuron. Journal of computational neuroscience, 10(1), 25-45. [PubMed:11316338] [WorldCat] [DOI] - ↑
Jolivet, R., Kobayashi, R., Rauch, A., Naud, R., Shinomoto, S., & Gerstner, W. (2008).
A benchmark test for a quantitative assessment of simple neuron models. Journal of neuroscience methods, 169(2), 417-24. [PubMed:18160135] [WorldCat] [DOI] - ↑
Levakova, M., Kostal, L., Monsempès, C., Lucas, P., & Kobayashi, R. (2019).
Adaptive integrate-and-fire model reproduces the dynamics of olfactory receptor neuron responses in a moth. Journal of the Royal Society, Interface, 16(157), 20190246. [PubMed:31387478] [PMC] [WorldCat] [DOI] - ↑
Kobayashi, R., & Shinomoto, S. (2007).
State space method for predicting the spike times of a neuron. Physical review. E, Statistical, nonlinear, and soft matter physics, 75(1 Pt 1), 011925. [PubMed:17358202] [WorldCat] [DOI] - ↑ 22.0 22.1 22.2
Yamauchi, S., Kim, H., & Shinomoto, S. (2011).
Elemental spiking neuron model for reproducing diverse firing patterns and predicting precise firing times. Frontiers in computational neuroscience, 5, 42. [PubMed:22203798] [PMC] [WorldCat] [DOI] - ↑ Gerstner, W. & Kistler, W.M. (2002).
Spiking neuron models: Single neurons, populations, plasticity., Cambridge: Cambridge University Press. PDF - ↑
Izhikevich, E.M. (2001).
Resonate-and-fire neurons. Neural networks : the official journal of the International Neural Network Society, 14(6-7), 883-94. [PubMed:11665779] [WorldCat] [DOI] - ↑
Gerstner, W., & Naud, R. (2009).
Neuroscience. How good are neuron models? Science (New York, N.Y.), 326(5951), 379-80. [PubMed:19833951] [WorldCat] [DOI] - ↑
Rossant, C., Goodman, D.F., Fontaine, B., Platkiewicz, J., Magnusson, A.K., & Brette, R. (2011).
Fitting neuron models to spike trains. Frontiers in neuroscience, 5, 9. [PubMed:21415925] [PMC] [WorldCat] [DOI]
![{\displaystyle \omega =10{\mbox{ }}[mV]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9645d3b8c92e78bbf326ff1775290427a8c6f780)
![{\displaystyle \alpha _{1}=4{\mbox{ }}[mV]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d07e83624d84f14798e3fe2e62f26b5eb2efba85)
![{\displaystyle E_{L}=0{\mbox{ }}[mV]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e9114c33adeab92321935ef6f8559e75b63cbf2)





















![{\displaystyle V_{th}=-50{\mbox{ }}[mV]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47d85c7ce8bfcc25484b6ec75bc6826fd530dbad)
![{\displaystyle V_{th}=-52{\mbox{ }}[mV]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ff668c7cbb5e9ab0fbec128ba47ff056a19a6f0)
![{\displaystyle I_{0}=0.151{\mbox{ }}[nA]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcca44043f3e67415b3bcf1cd37a9263f69d4d45)
![{\displaystyle \omega =24{\mbox{ }}[mV]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6aa341463307628531d713da730cc67128f98ee)