(4人の利用者による、間の102版が非表示) 1行目:
1行目: <div align="right">
フェルスター共鳴エネルギー移動(FRET) 英:Förster resonance energy transfer 英略称:FRET、独:仏:
<font size="+1">[http://researchmap.jp/read0068001 上田 善文]</font><br>
''金沢医科大学 血液免疫内科学''<br>
<font size="+1">[http://researchmap.jp/2rikenbsi 林 康紀]</font><br>
''独立行政法人理化学研究所 脳科学総合研究センター''<br>
DOI:<selfdoi /> 原稿受付日:2013年9月18日 原稿完成日:2014年4月7日<br>
担当編集委員:[http://researchmap.jp/michisukeyuzaki 柚崎 通介](慶應義塾大学 医学部生理学)<br>
</div>
英:[[Förster]] resonance energy transfer 英略称:FRET 独:Förster-Resonanzenergietransfer 仏:transfert d'énergie entre molécules fluorescentes
<br> FRETは、1946年、Theodor Försterによって報告された現象である<ref><pubmed>22352636</pubmed></ref>。Donor となる蛍光体の蛍光スペクトルとAcceptorとなる蛍光体の励起スペクトルに重なりがあるときに、DonorからAcceptorへのエネルギー移動が起きる。蛍光を伴わないエネルギー移動であることから、FRETは、一般的にFluorescence resonance energy transferとして用いられるがFörster resonance energy transferが正しい。GFPの改良に伴うバイオイメージングの発展によって、FRETを基にした細胞内シグナル伝達分子の可視化検出に用いられ、脳神経研究においても、細胞、スライスなどの組織、個体レベルで応用されている。
{{box|text= 二つの[[wj:蛍光|蛍光]]分子がごく近接して存在する場合、一つの蛍光分子からもう一つの蛍光分子へエネルギーが移行する。これをFörster共鳴エネルギー移動(FRET)という<ref name=ref1><pubmed>22352636</pubmed></ref>。FRETの効率は2つの蛍光分子の[[wj:スペクトル|スペクトル]]の重なりの大きさ、距離と角度により左右されるため、FRETを測定する事により蛍光分子間の空間配置を間接的に測定する事が可能である。特に近年の[[GFP]]ならびにその類縁タンパク質を用いた遺伝子にコードされるFRETプローブが作成され、タンパク質相互作用、生化学反応や細胞内シグナル伝達を可視化する事が出来るようになった。}}
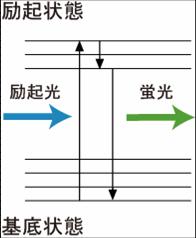
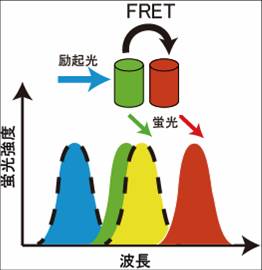
<br> [[Image :FRET図1.jpg|thumb|right|300px |<b >図1:ヤブロンスキーダイヤグラム </b >]] [[Image:FRET図3 .jpg|thumb|right|300px|<b>図2:励起光によって励起された光子が基底状態に戻る際の減衰曲線 </b>]] [[Image :FRET図2.jpg|thumb|right|300px |<b >図3 :Donorの蛍光スペクトルとAcceptorの励起スペクトルに重なりがあるときに、FRETが起きる。例としてAcceptorをGFP、DonorをRFPで表している。 </b >]]
==Förster共鳴エネルギー移動とは==
[[Image:FRET-図3.jpg|thumb|right|300px|<b>図1. ドナーとアクセプターの励起、蛍光スペクトル</b><br>ドナーの蛍光スペクトルとアクセプターの励起スペクトルに重なりがあるときに、FRETが起きる。黒破線で囲まれたスペクトルは、励起スペクトルを示す。緑色のタンパク質がドナー、赤色タンパク質がアクセプターを示す。]]
二つの蛍光分子がごく近接して存在する場合、一つの蛍光分子からもう一つの蛍光分子へ、エネルギーが移行する事が知られている(図1)。この現象は、1946年[[w:Theodor Förster|Theodor Förster]]によって報告されたことから、Förster共鳴エネルギー移動(FRET)という<ref>'''Förster, T.'''<br>Energiewanderung und Fluorescenz<br>''Naturwissenscaft''. 1946, 33:166–175</ref> <ref name=ref1 />。かつてFRETは、fluorescence resonance energy transferの略称として用いたが、実際には蛍光を伴わないエネルギー移動であることから、現在ではFörster resonance energy transferと呼ぶ事がIUPACにより推奨されている。
かつては生細胞にてFRETを検出するのは、非常に煩雑であった。プローブとなるタンパク質を精製、化学的に[[wj:蛍光色素|蛍光色素]]でラベルし、細胞に導入するという操作が必要であり、生物学分野での応用はきわめて限定されたものであった。しかし、GFPとその変異体、類縁タンパク質の発見により今日においては様々な分野において、多くの蛍光タンパク質を基にした、完全に遺伝子によってコードされるFRETプローブが使用されている。
== 原理 ==
==FRETの効率を決定する因子==
図1のヤブロンスキーダイヤグラムのように、Donorの蛍光団の電子が、励起光により基底状態から励起状態に励起される。励起された電子は、回転エネルギーや振動エネルギーを失いながら、励起状態の底まで行き着く。その後、基底状態に戻る際に、蛍光としてエネルギーを放出する。蛍光の減衰曲線は、速度定数を<math>k \ </math>として、図2のように表すことができる。今、Donorの近傍(数nmオーダー)に、Donorの蛍光スペクトルと重なる励起スペクトルを持ったAcceptorが存在するとFRETが起きる(図3)。FRETの起きる速度を<math>k_f \ </math>とすると、Donorの蛍光速度は<math>k-k_f \ </math>となり、蛍光寿命の減少、Donorの蛍光強度の減少、Acceptorの蛍光の増加などが観察される。 <br> FRETの速度定数<math>k_f \ </math>は、以下の式で規定される。
蛍光分子のうち、エネルギーを受け渡す方をドナー、受け取る方をアクセプターと呼ぶ。FRETの効率はドナーとアクセプター間の次のような因子によって影響される。
<br> <math>k_f(r,\kappa) = \frac{k_DQ_D\kappa^2}{r^6}\left(\frac{9000(In10)}{128\pi^5Nn^4}\right)\int_0^\infty F_D(\lambda)\epsilon_A(\lambda)\lambda^4\,d\lambda</math>
* ドナーとアクセプター間の距離 ''r''
<br> ここで、<math>k_D \ </math>はDonor蛍光の速度定数、<math>Q_D \ </math>はDonorの蛍光の量子収率、<math>\kappa \ </math>はDonorとAcceptorの双極子モーメントの相対的関係、<math> r \ </math>はDonorとAcceptorの距離、<math>N \ </math>はアボガドロ数、<math>n \ </math>は溶媒の屈折率、<math>F_D \ </math>は規格化したDonorの発光強度、<math>\epsilon_A \ </math>はAcceptorのモル吸光係数。
* ドナーの発光スペクトルとアクセプターの吸収スペクトルの重なり ''J''
<br> 実際に、変数となりうるのは以下の性質である。 <br> 1.距離<math>r \ </math>。式が示すように距離の6乗に反比例する。FRET効率が50%になるときの距離を、フェルスター距離(Förster distance)という。 <br> 2.Donorの蛍光の遷移双極子モーメントとAcceptorの遷移励起光のための双極子モーメントの相対配向。フルオレセインなど、等方的に蛍光の放射が起きる場合には、<math>\kappa^2 \ </math>=<math>\tfrac{2}{3} \ </math>であるが、GFPをはじめとした配向の定まった蛍光タンパク質などは各々の値を取る。
* ドナーの発光双極子モーメントとアクセプターの吸収双極子モーメントとの相対分子配向''κ''
<br>
ドナーとアクセプター蛍光分子が決定されると''J''は次のように計算される。
== 検出 ==
<br>
: <math> J = \int f_{\rm D}(\lambda) \, \epsilon_{\rm A}(\lambda) \, \lambda^4 \, d\lambda </math>
=== ドナーとアクセプターの蛍光強度を測定する方法 ===
FRETが起きると、Donorの蛍光強度が減少し、Acceptorの蛍光強度が増加する。測定の際には蛍光強度の変化を測定することになるが、細胞などの試料においては、細胞の形状変化に伴う蛍光強度変化などが起きることから、実際にはドナーとアクセプターの蛍光強度のの変化を取得することによって、これらのファクターを除外する。
ここでf<sub>D</sub>(λ)はピーク値を1としたドナー発光スペクトル、 ε<sub>A</sub>(λ)はアクセプターの[[wj:モル吸光係数|モル吸光係数]]、λは波長である。
=== ドナーの蛍光寿命を測定する方法 ===
''J''を用い特定のドナーとアクセプターの間にFörster距離''R<sub>0</sub>''が以下のように定義される。これはエネルギー移動効率が50%となるドナーとアクセプターの距離である。通常の蛍光分子の場合、5 nm程度である。
近年、時間相関単一光子計数法とpulsing laserの相性の良さから、時間分解能の向上により、蛍光寿命を比較的短時間で取得することが可能となった。 蛍光寿命は、GFPおよびそのcolor variantタンパクでは、1-5 nsec、希土類錯体などは、1µsec、pyren coronenなどは、400, 200 nsecである。上述のように、FRETが起きると蛍光寿命を表す減衰曲線の傾きが変わる。これを基にFRETを観察する。
=== Anisotropyを測定する方法 ===
: <math> {R_0}^6 = \frac{9\,Q_0 \,(\ln 10)}{128 \, \pi^5 \,n^4 \, N_A} \kappa^2 \, J</math>
一つの蛍光団のストークスシフトが小さい場合、励起スペクトルと蛍光スペクトルの重なりが大きい。このような蛍光団では、同一の蛍光団同士で、Homo-FRETが生じる。Homo-FRETは、蛍光強度および蛍光寿命は変化しないが、異方性が変わる。この原理を用いて、一般的には、分子同士のクラスターの度合いなどに応用されている。
<br>
''κ''はドナーとアクセプターの相互分子配向である。多くの場合、正確に求める事は困難であるため、しばしば''κ''<sup>2</sup> =2/3 と仮定される。この値は、両方の色素が自由に回転しており、励起状態の間は等方的に配向していると考えられる場合に得られる。色素が固定されている場合や自由に回転することができないような場合、''κ''<sup>2</sup> =2/3 とは仮定できない。''Q<sub>0</sub>''はアクセプターが無い場合のドナーの蛍光[[wj:量子収率|量子収率]]、''n''は媒体の[[wj:屈折率|屈折率]](水、25 °Cの場合、1.3342)、''N<sub>A</sub>''は[[wj:アボガドロ数|アボガドロ数]]である。これらの定数を当てはめると、''κ''より前の部分は、8.786 x 10<sup>11</sup> mol L<sup>-1</sup> cm nm<sup>2</sup>となる<ref><pubmed> 10964438</pubmed>但しこの論文にはミスプリが有り、p. 439で''κ''<sup>2</sup> とすべき所を、''κ''としている。</ref>。
<br >
''R<sub>0</sub>''を用いると、FRET効率''E''は次のように表す事が出来る。
<br >
== 神経科学分野への応用 ==
: <math>E=\frac{1}{1+(r/R_0)^6}\!</math>
<br> 1992年、緑色蛍光タンパク質(Green fluoresent protein : GFP)のクローニングに始まり、青色蛍光タンパク質CFP、黄色蛍光タンパク質YFPなどの開発以来、FRETは積極的に細胞内イメージングに取り入れられ始めた。1997年、宮脇、Tsienらによって、CFPおよびYFPを利用した、Calcium indicator, Cameleonが開発され <ref ><pubmed>9278050</pubmed></ref>、さらに、cAMP, cGMP<ref><pubmed>11140757</pubmed></ref>, リン酸化を初めとした主要な細胞内シグナル伝達子のFRETプローブが次々と作製され、細胞内の活性の局在などの解明に大きく貢献した。 <br> 脳神経分野においては、高雄、林らが、2000年初期に記憶の形成に必須なシグナル分子、カルシウムカルモデュリンキナーゼII (CaMKII)の活性化プローブ開発し分散培養系にてCaMkIIの可視化に成功した<ref><pubmed>15788767< /pubmed></ref>。 <br> 1990年代後半、Svobodaらによって、2光子顕微鏡が脳神経科学に導入され、神経回路ネットワークを保持したスライスおよび個体の生きた脳の神経活動を観察可能になった。岡本、林らは、神経細胞の連結部位、シナプスのシナプス後膜(スパイン)において、その形態を制御するactinの重合を可視化するためのFRETプローブを開発した<ref><pubmed>15361876</pubmed></ref>。一方、脳のスライスにおいては、波長依存的な蛍光の吸収が生じるため、DonorとAcceptorの2波長を測定する蛍光強度比を測定するよりも、蛍光の散乱、吸収によって変化しない蛍光寿命測定法が導入された。安田、Svobodaらは、蛍光寿命測定を基に、スパインの構造的変化を誘導するRas,cdc42,RhoAなどのシグナル伝達分子の活性化の変化を観察することに成功している<ref><pubmed>19295602</pubmed></ref><ref><pubmed>18556515</pubmed></ref><ref><pubmed>21423166</pubmed></ref>。 <br> 個体においてもFRET測定法が導入されている。神経回路ネットワークにおけるシナプスの役割を解明する目的で、フェレットの大脳皮質視覚野にCaMKIIプローブを発現し、片眼剥奪によって、神経回路ネットワークに変化を起こした時のCaMKIIの活性化の変化を観測している<ref><pubmed>22160721</pubmed></ref>。また、神経活動をモニターする目的で、Knöfelらは、膜電位プローブVSFP2.3/2.42を開発し、マウスのヒゲ刺激の入力先であるbarrel cortexでの入力特異的な神経の活性化を観察している。 <br> 病態との関係では、神経細胞内のカルシウム濃度を測定するために、オレゴングリーンの蛍光寿命の変化から、カルシウム濃度を測定し、アストロサイトでのカルシウム濃度が、アルツハイマー様マウスと正常マウスで違うことが報告されている<ref><pubmed>19251629</pubmed> </ref >。
Homo-FRETも応用されている。CaMKIIは12量体を形成しているが、異方性の変化を基に、その構造中にdimerの単位が存在し、活性化に伴うdimer同士の位置関係が変化することをvogelらが明らかにしている<ref><pubmed>19339497</pubmed></ref>。
Förster距離''R<sub>0</sub>''が大きいドナーとアクセプターの組み合わせの方が、FRET効率''E''が良い。''R<sub>0</sub>''を大きくするためには蛍光量子収率''Q<sub>0</sub>''がよいドナー、モル吸光係数''ε<sub>A</sub>(λ)''が良いアクセプター、またいずれも長波長域にあるドナーとアクセプターの組み合わせを選択する。
<br>
ドナーとアクセプターの蛍光スペクトルが変化しない状態では、ドナーとアクセプター間の距離''r''と配向''κ''の変化をFRETの効率の変化として読み取る事が出来る。これを利用して、様々な細胞現象に対するプローブをデザインする事が可能である。
==FRETの画像検出==
FRETが起こるとドナーの蛍光強度の減少、アクセプターの蛍光の増加、ドナー蛍光寿命の減少が観察される。液体サンプルであれば[[wj:蛍光分光光度計|蛍光分光光度計]]を用いる事で検出する事が可能であるが、画像として取得する場合には観察したい対象の特性を考慮しつつ、方法を選択していく。
===蛍光強度比イメージング===
ドナーおよびアクセプターの蛍光を取得し、ピクセルごとの蛍光強度比を計算する。FRETが起きると、ドナーの蛍光強度が減少し、アクセプターの蛍光強度が増加する。現在、最も広く使用されている手法である。[[タイムラプス解析]]も行える。
ドナー蛍光強度とFRET効率Eとは次のような関係に有る。
: <math> E = 1 - {F\,'_{\rm D}}/{F_{\rm D}} \!</math>
ただし、F'<sub>D</sub>、F<sub>D</sub>はそれぞれ、アクセプターがある場合と無い場合でのドナー蛍光強度である。つまり、FRET効率が良い程、F'<sub>D</sub>小さくなる、つまり画像が暗くなる。一方で、FRETによりアクセプター画像は明るくなるので、ドナー画像とアクセプター画像の比を計算する事で、FRETを検出する事が出来る。
データを取得、解釈する際に注意しなければいけないポイントがある。
まず、ドナーの蛍光のアクセプターチャネルへの漏れ込みであり、信号/雑音比の減少の原因となる。漏れ込みを極力抑えるには、適切な[[wj:バンドパスフィルター|バンドパスフィルター]]を用いる。光量を犠牲にしても、ドナー蛍光が漏れ込まない波長を選ぶ方がFRETは特異的に検出できる。
また、蛍光画像に背景雑音がある事があるが、それがFRET変化に影響を与える。FRETの計算の際に背景雑音を引き算しなければならないが、蛍光シグナルが暗いと、少しの背景雑音のぶれがシグナルを左右する。例えば細胞の周辺は暗いので背景雑音の引き算により[[wj:偽陽性|偽陽性]]が出やすいので注意を要する。
2分子間FRETのイメージングでは、ドナーとアクセプターの局在の違いは偽陽性を生じる。リンカーで連結し1分子にするか、局在しているアクセプターの蛍光強度を補正することで避けることが可能である。
=== アクセプター褪色法 ===
適切な波長の光によって、アクセプターを褪色させることでFRETを解消することができる。つまり、F'<sub>D</sub>がアクセプターの褪色によりF<sub>D</sub>と等しくなる事により、E=0となる。その為、褪色前後の画像を比較する事によりEが検出可能である。しかしながら、この手法は不可逆的であるために経時的変化を追うことは困難である。
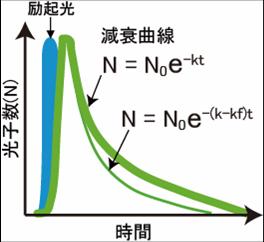
[[Image:FRET-図2new.jpg|thumb|right|300px|<b>図2:励起光によって励起された電子が基底状態に戻る際の減衰曲線</b><br>緑の太い線がFRETが起きていない時のドナー蛍光の減衰曲線。FRETを起こしたドナー蛍光の速度が加わることにより速度定数が大きくなり細い緑の線のように減衰曲線の傾斜が大きくなる。 ''N<sub>0</sub>''は励起光によって励起された電子の数、''k''は励起状態にある電子が基底状態に戻る速度定数。]]
=== 蛍光寿命イメージング===
蛍光体が励起されると、図2に示すような減衰曲線に従って蛍光を発する。蛍光寿命は、''k''は励起状態にある電子が基底状態に戻る速度定数''k''の[[wj:逆数|逆数]]である。蛍光として基底状態に戻る際の速度定数、熱を発して基底状態に戻るなどの無放射遷移の速度定数の和として表される。
FRETを起こしている時の速度定数''k<sub>f</sub>''は、以下の式で規定される。
:<math>k_f(r,\kappa) = \frac{k_DQ_D\kappa^2}{r^6}\left(\frac{9000In10}{128\pi^5n^4N_A}\right)J</math>
ここで、''k<sub>D</sub>''はドナーの蛍光の速度定数である。
ドナー蛍光の速度定数とFRET効率Eとは次のような関係に有る。
: <math> E = 1 - {\tau'_{\rm D}}/{\tau_{\rm D}} \!</math>
ここで''τ'<sub>D</sub>''と''τ<sub>D</sub>''はそれぞれ、アクセプターが存在する場合と存在しない場合でのドナー蛍光寿命である。つまり、FRETが起きると、蛍光寿命が短縮する(図3)。
蛍光寿命測定法は、アクセプターの蛍光は必要ないため、蛍光強度比測定法に比べて、蛍光の漏れ込み、ドナーとアクセプターの局在の違いなどによって生じる疑陽性を回避できる。
蛍光寿命の変化を測定する方法は2つある。
[[Image:FRET-図4.jpg|thumb|right|300px|<b>図3. [[海馬]][[スライス]][[CA1]][[錐体細胞]]に発現させたGFPの蛍光寿命イメージおよび減衰曲線</b><br>(横軸は時間、縦軸は光子数)。実際には、20秒で数千個オーダーの光子を取得する。これらの光子の発生確率分布が減衰曲線を形成し、近似曲線をフィッティングさせることで蛍光寿命を取得する。]]
====時間ドメイン====
励起光によって発生した一つ一つの光子が検出器まで届くまでの時間(数nsec)を計測することで時定数τを計算する。時間を横軸としてヒストグラムを作製することができる。通常蛍光寿命は指数関数に従い減衰していく(図3)。FRETを起こしている分子と起こしていない分子が共存する時には[[wj:二重指数関数|二重指数関数]]になるため、二重指数関数にフィッティングすることによって、FRETの起きている分子の割合が算出できる。得られる光子の数が少ない時には二重指数関数フィッティングは不正確になりやすい為、単に平均蛍光寿命を計算するだけで済ませる場合も有る。単一指数関数の場合は、平均蛍光寿命はτに等しくなる。
理論上は取得した蛍光を全てデータに反映させることができるが、実際には光子取得後、再び光子を取得する状態に戻るハードウェアのリセット時間(dead time)などがあり全ての光子を取得する事は出来ない。また、秒単位の経時変化を追うためには、低解像度で画像取得されているのが現状で有り、多数のピクセルから蛍光寿命を取得するためには、処理速度の速いハードウェアが必要となる。
光源には[[wj:パルスレーザー|パルスレーザー]]を用いる。神経系の研究によく用いられる[[二光子顕微鏡]]に後付けする事も可能である。
[[File:FRET-Heterodyning.png|thumb|right|300px|<b>図4. 周波数ドメインによる測定</b><br>光源の強度を高周波で変調させるのと同時に、検出器も高周波で変調させる。その時に光源の周波数(f<sub>ex</sub>)と検出器の周波数(f<sub>s</sub>)をずらし、そこから蛍光寿命を計算により求める。]]
====周波数ドメイン====
光源の強度を高周波で変調させるのと同時に、検出器も高周波で変調させる。その時に光源と検出器の周波数をずらしておく(heterodyning)(図4)。多数のサイクルを繰り返す事により、間接的に蛍光寿命を計算していく。画像の取得にかかる時間が時間ドメインと比較して短いのが特徴である。
時間ドメインと同様に光源にはパルスレーザーや光量が高頻度にて変調できるレーザーなどが用いられる。
===異方性測定===
一つの蛍光団の[[wj:ストークスシフト|ストークスシフト]]が小さい場合、励起スペクトルと蛍光スペクトルの重なりが大きいような蛍光団では、同一の蛍光団同士で、[[wikipedia:Homo-FRET|Homo-FRET]]が生じる。Homo-FRETは、蛍光強度および蛍光寿命は変化しないが、[[wj:異方性|異方性]]が変わる。この原理を用いて分子同士のクラスターの度合いなどに応用されている。
== プローブのデザイン ==
[[ファイル:FRET Probes.png|thumb|right|350px|'''図5. 様々なフレットプローブの類型'''<br>]]
GFPとその変異体、類縁タンパク質の発見により今日においては様々な細胞生物学の分野において、多くの蛍光タンパク質を基にしたFRETプローブが使用されている。
これらのプローブを分類すると、以下のように分類される(表1、図5)。
===プローブの分解に伴うFRETの変化を検出するプローブ===
この原理は、FRETプローブの最も初期に導入されたデザインである(図5A)。プロテアーゼによって分解される配列の両端にドナーとアクセプターを連結する。プロテアーゼによって、この配列が分解されるとドナーとアクセプターの間に起きていたFRETが解消されることによって、プロテアーゼの活性を評価する。例として、[[wj:第X因子|第X因子]]、[[カスパーゼ]]などの[[プロテアーゼ]]活性のプローブが挙げられる<ref name=ref5><pubmed>8707050</pubmed></ref> <ref name=ref6><pubmed>9518501</pubmed></ref> <ref name=ref7><pubmed>12409609</pubmed></ref> <ref name=ref8><pubmed>21637712</pubmed></ref> <ref name=ref9><pubmed>17946841</pubmed></ref>。このプローブのデザインの短所としては、反応が不可逆的であるために、一つの実験系で何度も測定することが困難であることである。
===二分子間相互作用を利用したFRETプローブ===
興味のあるタンパク質同士の相互作用を測定する際に、この原理が用いられる。一方にドナー、他方にアクセプターを連結する。タンパク質同士が結合していないときにはFRETは起きていないが、結合することによってFRETを生じる(図5B)。
距離のファクターを生かせるために、比較的大きなシグナルが得られる一方、内在性のタンパク質が反応に関与するために、その分FRET応答が減少する。ドナーとアクセプターの発現量の差によるFRETの応答の変化も問題になる。特に、アクセプターと結合しないドナーが多量に存在するとFRET応答が小さくなる。一般にアクセプターが多い系が、使用に適している。
タンパク質相互作用を測定する事により間接的にシグナル伝達系の活性化も測定する事が可能である。例えば、[[低分子量Gタンパク質]]が活性化に伴い、エフェクタータンパク質と相互作用が起こる事を利用し、低分子量Gタンパク質活性を測定する事が可能である。
また、タンパク質相互作用はポリマーでも良い。これを利用して[[アクチン]]の重合状態の測定にも用いられた<ref name=ref10><pubmed>15361876</pubmed></ref>(図5C)。
===一分子内FRETプローブ===
一分子内にドナーとアクセプターを連結し、これらの配向および距離の変化を利用する。2分子間FRETに生じるような発現量の違いやドナーとアクセプターの局在の変化によって生じる疑似陽性を考慮する必要がない。さらに活性に伴うタンパク質の構造変化などを利用するために、比較的容易に応答するプローブが作製できるが、ドナーとアクセプターを適切な位置に配置するなどの検討が必要である。
====タンパク質の構造変化====
興味のあるタンパク質が、活性化の際に構造変化を誘起することが知られている場合には構造変化を利用することができる(図5D)。タンパク質のC末およびN末にドナーおよびアクセプターを連結する。あるいは構造変化が起こすドメインの方が、FRETは起こりやすい可能性もある。この手法は、[[CaMKII]]<ref name=ref11><pubmed>15788767</pubmed></ref>、[[カルシニューリン]]<ref name=ref12><pubmed>18493642</pubmed></ref>、[[raf]]<ref name=ref13><pubmed>15711535</pubmed></ref> <ref name=ref14><pubmed>16858395</pubmed></ref>、[[膜電位]]測定<ref name=ref15><pubmed>18622396</pubmed></ref>、などに用いられている。
====リガンド結合に伴う構造変化====
ある種のタンパク質は[[リガンド]]に結合する事に活性が調節される。リガンド結合を検出するようにFRET構築を工夫する(図5E)。
例えば[[カルシウム]]FRETプローブ、カメレオンはこの原理を利用している<ref name=ref16><pubmed>9278050</pubmed></ref>。 この場合、ドナー、[[カルモジュリン]]、カルモジュリン結合配列であるM13ペプチド、アクセプターを1つの分子に融合する。カルモジュリンがCa<sup>2+</sup>と結合すると、M13ペプチドと結合し、蛍光強度が変化する。
また、[[低分子量Gタンパク質]]の活性化プローブは、低分子量Gタンパク質、シグナル伝達下流の結合タンパク質の結合ドメインをドナーとアクセプターで挟んだ形状をしている(図5E)。低分子Gタンパク質が[[GDP]]から[[GTP]]結合型になり活性化すると、結合ドメインと相互作用によりFRETが生じる<ref name=ref17><pubmed>16429133</pubmed></ref>。
====共有結合修飾によって生じる構造変化====
このプローブは、ドナー、アクセプター、[[wj:共有結合|共有結合]]修飾を受けるドメイン、これを認識するドメインからなる。プローブが共有結合修飾を受けると、認識するドメインが結合し、ドナーとアクセプターの距離が縮まりFRETが起きる(図5F)。
このプローブは、[[キナーゼ]]の活性化を測定するために使用される<ref name=ref18><pubmed>11875431</pubmed></ref> <ref name=ref19><pubmed>11752449</pubmed></ref>。この場合、キナーゼの基質となるタンパク質に[[14-3-3タンパク質]]のような[[リン酸化]]タンパク質を認識するドメインを融合し、その結合に伴うタンパク質構造変化を、両端に結合させたドナーとアクセプター間のFRETで測定する。
====生体膜上の小分子====
このプローブは、主に、[[wj:脂質|脂質]]分子に応用されてきた(図5G)。ドナー、脂質結合ドメイン、アクセプターがヘリックス構造で連結され、[[グリシン]]-グリシン配列をその途中に導入することで、そこを中心に一方の蛍光タンパク質が回転することができる。膜結合ドメインを用いて、プローブを結合させる。脂質分子が増えた際に、脂質結合ドメインが脂質分子を認識し、構造変化が起き、ドナーとアクセプターの距離が縮まりFRETが生じる。[[ジアシルグリセロール]]<ref name=ref20><pubmed>16990811</pubmed></ref>、[[ホスファチジルイノシトール|イノシトールリン脂質]]群<ref name=ref21><pubmed>14528311</pubmed></ref> <ref name=ref18685081><pubmed>18685081</pubmed></ref>を測定するために用いられている。
{| class="wikitable"
|+ 表1.様々なFRETプローブ
|-
| 分類||対象||プローブ名||年||プローブデザイン||参考文献
|-
|rowspan="21" | 生体内小分子|| [[カルシウム]] ||Cameleon|| 1997 || E || <ref name=ref16 />
|-
|[[サイクリックGMP]] ([[cGMP]]) ||CGY, Cygnet, pGES-DE2, cGi|| 2000, 2001, 2006 ||D || <ref name=ref11140757><pubmed>11140757</pubmed></ref><ref><pubmed>11226257</pubmed></ref><ref><pubmed>16369548</pubmed></ref><ref><pubmed>23801067</pubmed></ref>
|-
|[[サイクリックAMP]] ([[cAMP]]) ||Epac|| 2000,2004 || B, D || <ref><pubmed>11872839</pubmed></ref><ref><pubmed> 15231839</pubmed></ref>
|-
|[[イノシトール3リン酸]] ([[IP3|IP<sub>3</sub>]]) ||LIBRA, Fretino, FIRE|| 2004, 2005, 2006 || D || <ref><pubmed>15272011</pubmed></ref><ref><pubmed> 16053285</pubmed></ref><ref><pubmed> 16754959</pubmed></ref>
|-
|[[一酸化窒素]] ([[NO]]) ||NOA-1, Piccell|| 2005, 2006 || その他 || <ref><pubmed>16176986</pubmed></ref><ref><pubmed> 17165805</pubmed></ref>
|-
|[[アデノシン3リン酸]] ([[ATP]]) ||A Team 1.03-nD/nA|| 2012 || D || <ref><pubmed>19720993</pubmed></ref>
|-
|[[エストロゲン]] ||SCCoR|| 2004 || D || <ref><pubmed>15080726</pubmed></ref>
|-
|[[アンドロゲン]] ||Ficaro|| 2006 || E || <ref><pubmed>16555356</pubmed></ref>
|-
|[[グルココルチコイド受容体]]リガンド ||GLUCOCOR|| 2007 || B, E || <ref><pubmed>15163683</pubmed></ref><ref><pubmed>17897691</pubmed></ref>
|-
|[[神経成長因子]] ||ECaus|| 2008 || F|| <ref><pubmed>18510313</pubmed></ref>
|-
|[[核内受容体]] ||conpro|| 2007 || E || <ref><pubmed>17387660</pubmed></ref>
|-
|[[O-N-アセチルグルコサミン]] ([[O-GlcNAc]]) || || 2006 || F || <ref><pubmed>17105262</pubmed></ref>
|-
|[[ビタミンA]] ([[レチノイン酸]]) ||GEPRAS|| 2013 || D || <ref><pubmed>23563268</pubmed></ref>
|-
|[[wj:モリブデン酸|モリブデン酸]] ||MolyProbe|| 2013 || B || <ref><pubmed>23472155</pubmed></ref>
|-
|[[グルタミン酸]] ||FLIPE|| 2005 || D || <ref><pubmed>15939876</pubmed></ref>
|-
|[[wj:亜鉛|Zn<sup>2+</sup>]] ||eCALWY-1|| 2009 || D || <ref><pubmed>19718032</pubmed></ref>
|-
|[[wj:塩素|Cl<sup>-</sup>]] ||Clomeleon|| 2000 || その他 || <ref><pubmed>11055428</pubmed></ref>
|-
|[[wj:水素イオン濃度|水素イオン濃度]] (pH) ||GFpH, YFpH|| 2001 || その他 || <ref><pubmed>11716495</pubmed></ref>
|-
|[[wj:グルコース|グルコース]] ||FLIPglu|| 2003 || D || <ref><pubmed>12649277</pubmed></ref>
|-
|[[wj:マルトース|マルトース]]||FLIPmal|| 2002 || D || <ref><pubmed>12097642</pubmed></ref>
|-
|[[wj:リボース|リボース]]||FLIPrib|| 2003 || D || <ref><pubmed>14550551</pubmed></ref>
|-
|rowspan="25" | タンパク質リン酸化酵素 || [[カルシウム/カルモジュリン依存性タンパク質リン酸化酵素II]] ([[CaMKII]]) ||Camui α, green-Camui α, Camk2a reporter|| 2005, 2009, 2011, 2013 || D || <ref name=ref11 /> <ref name=ref19295602><pubmed>19295602</pubmed></ref> <ref name=ref23602566><pubmed> 23602566</pubmed></ref> <ref name=ref21506563><pubmed> 21506563</pubmed></ref>
|-
| [[Src]] ||Srcus|| 2005, 2005, 2007 || F || <ref name=ref19 /> <ref><pubmed> 15846350</pubmed></ref><ref><pubmed> 17284441</pubmed></ref>
|-
| [[Ca2+/リン脂質依存性タンパク質リン酸化酵素|Ca<sup>2+</sup>/リン脂質依存性タンパク質リン酸化酵素]] ([[Cキナーゼ]], [[プロテインキナーゼC]], [[PKC]]) ||CKAR, CY-PKCdelta|| 2003, 2005 || D, F || <ref><pubmed>12782683</pubmed></ref><ref><pubmed> 15611119</pubmed></ref>
|-
| [[タンパク質リン酸化酵素D]] ([[Dキナーゼ]], [[プロテインキナーゼD]], [[PKD]]) ||DKAR|| 2007 || F || <ref><pubmed>17189263</pubmed></ref>
|-
| [[cAMP依存性タンパク質リン酸化酵素]] ([[Aキナーゼ]], [[プロテインキナーゼA]], [[PKA]]) ||ART, AKAR|| 2000, 2001 || F || <ref><pubmed>10700148</pubmed></ref><ref><pubmed>11752448</pubmed></ref>
|-
| [[Abl]] ||Picchu|| 2001 || F || <ref name=ref19 />
|-
| [[Bcr]]-Abl ||Bcr-Abl activity sensor||2010 || F || <ref><pubmed>20817824</pubmed></ref>
|-
| [[c-Raf]] ||Prin-cRaf|| 2005 || D || <ref name=ref13 />
|-
| [[P21 protein-activated kinase 1]] ([[PAK1]]) ||Pakabi|| 2009 || D || <ref><pubmed>19574218</pubmed></ref>
|-
| [[B-raf]] ||Prin-Braf|| 2006 || D || <ref name=ref14 />
|-
| [[Zeta-chain-associated protein kinase 70]] ([[ZAP-70]]) ||ROZA|| 2008 || F || <ref><pubmed>18231606</pubmed></ref>
|-
| [[Akt]] ||Aktus, BKAR, Akind|| 2003, 2005, 2007 || F || <ref><pubmed>12773546</pubmed></ref><ref><pubmed> 15583002</pubmed></ref><ref name=ref17407381><pubmed> 17407381</pubmed></ref>
|-
| [[細胞外シグナル調節キナーゼ]] ([[Extracellular signal-regulated kinases]], [[ERK]]) ||Miu2, Erkus, EKAR|| 2006, 2007, 2008 || D, F || <ref><pubmed>16418172</pubmed></ref><ref><pubmed> 17261026</pubmed></ref><ref><pubmed> 19033456</pubmed></ref>
|-
| [[インシュリン受容体]] ||Phocus|| 2002 || F || <ref name=ref18 />
|-
| [[上皮成長因子受容体]] ([[EGFR]]) || ||2001 || F || <ref name=ref19 />
|-
| [[Ataxia telangiectasia mutated]] ([[ATM]]) || || 2007 || F || <ref><pubmed>17428747</pubmed></ref>
|-
|[[オーロラBキナーゼ]] || || 2008 || F || <ref><pubmed>18463638</pubmed></ref>
|-
| [[サイクリンB1]]-[[サイクリン依存性キナーゼ1]] || || 2010 || F || <ref><pubmed>20412769</pubmed></ref>
|-
| [[ミオシン軽鎖キナーゼ]] ||MLCK-FIP || 2002 || D || <ref><pubmed>11815633</pubmed></ref>
|-
| [[c-Jun N端末キナーゼ]] ([[JNK]]) ||JNKAR1, JUNKAR1EV || 2010, 2011 || F || <ref><pubmed>20212108</pubmed></ref><ref name=ref21976697><pubmed> 21976697</pubmed></ref>
|-
| [[リボソームS6キナーゼ]] ([[RSK]], [[S6K]]) ||Eevee-RSK, Eevee-S6K|| 2011 || F || <ref name=ref21976697></ref>
|-
| [[接着斑キナーゼ]] ([[Focal Adhesion Kinase]], [[FAK]]) ||CYFAK413, FERM-sensor|| 2008, 2009 || B, D || <ref><pubmed>17967873</pubmed></ref><ref><pubmed> 19208768</pubmed></ref>
|-
| [[Polo様キナーゼ1]] ([[polo-like kinase1]], [[PLK1]]) || || 2008 || F || <ref><pubmed>18615013</pubmed></ref>
|-
| [[ストレス活性化プロテインキナーゼ3]] ([[Stress-Activated Protein Kinase Kinase Kinase]], [[stress-activated protein kinase 3]], [[SAP3K]]) || || 2009 || F || <ref><pubmed>19737916</pubmed></ref>
|-
| [[細胞死関連タンパク質キナーゼ]] ([[death associated protein kinase 1]], [[DAPK1]]) ||DAPK1(334)-F40|| 2011 || D || <ref name=ref21506563 />
|-
| [[ホスファターゼ]] || [[カルシニューリン]] ||CaNAR1|| 2008, 2013 || D || <ref name=ref23602566 /><ref name=ref12 />
|-
|rowspan="8" | [[低分子量Gタンパク質]] || [[Ras]] ||Raichu-Ras, Fras|| 2001, 2006 || B, E || <ref name=ref17 /> <ref name=ref11429608><pubmed> 11429608</pubmed></ref>
|-
| [[Rap]] ||Raichu-Rap|| 2001 || E || <ref name=ref11429608></ref>
|-
| [[Rac]] ||Raichu-[[Rac1]]|| 2004 || E || <ref name=ref14570905><pubmed>14570905</pubmed></ref>
|-
| [[Rab5]] ||Raichu-Rab5|| 2008 || E || <ref><pubmed>18385674</pubmed></ref>
|-
| [[Rho]] ||Raichu-RhoA|| 2003, 2011 || B, E || <ref name=ref21423166><pubmed>21423166</pubmed></ref> <ref><pubmed> 12860967</pubmed></ref>
|-
| [[Cdc42]] ||Raichu-cdc42|| 2004, 2011 || B, E || <ref name=ref14570905 /><ref name=ref21423166 />
|-
| [[Ral]] ||Raichu-Ral|| 2004 || E || <ref><pubmed>15034142</pubmed></ref>
|-
| [[TC10]] ||Raichu-TC10|| 2006 || E || <ref><pubmed>16950130</pubmed></ref>
|-
|rowspan="6" | [[シグナル伝達]] || [[RCC1]]||CFP-RCC1-YFP|| 2008 || D || <ref><pubmed>18762580</pubmed></ref>
|-
| [[CrkII]][[リン酸化]] ||Picchu|| 2001 || F || <ref><pubmed>11406630</pubmed></ref>
|-
| [[neuronal Wiskott–Aldrich syndrome protein]] ([[N-WASP]]) ||Stinger|| 2004 || D || <ref><pubmed>15084285</pubmed></ref><ref><pubmed> 14732696</pubmed></ref>
|-
| [[アドレナリン受容体]] ||α<sub>2A</sub>[[AR]]-cam|| 2003 || D|| <ref name=ref12808462><pubmed>12808462</pubmed></ref>
|-
| [[副甲状腺ホルモン受容体]] ||PTHR-cam|| 2003 || D || <ref name=ref12808462 />
|-
| [[細胞膜]][[カルシウムポンプ]] ||BFP-PMCA-GFP|| 2007 || D || <ref><pubmed>17901055</pubmed></ref>
|-
| [[アセチル化]] || [[ヒストン]]アセチル化 ||Histac|| 2004, 2009 || F|| <ref><pubmed>15137760</pubmed></ref><ref><pubmed> 19805290</pubmed></ref>
|-
|rowspan="6" | [[脂質]] || [[ホスファチジルイノシトール-3,4,5-三リン酸]] ([[PIP3|PIP<sub>3</sub>]]) ||Fllip, FLIMPA|| 2003 || G || <ref name=ref21 />
|-
| [[ホスファチジルイノシトール-4,5-二リン酸]] ([[PIP2|PI(4,5)P<sub>2</sub>]]) ||Pippi-PI(4,5)P<sub>2</sub>|| 2008 || G || <ref name=ref18685081 />
|-
| [[ホスファチジルイノシトール-3,4-二リン酸]] ([[PI(3,4)P2|PI(3,4)P<sub>2</sub>]]) ||Pippi-PI(3,4)P<sub>2</sub>|| 2008 || G || <ref name=ref18685081 />
|-
| [[ホスファチジルイノシトール-4-リン酸]] ([[PI4P|PI4P]]) ||Pippi-PI(4)P|| 2008 || G || <ref name=ref18685081 />
|-
| [[ホスファチジン酸]] ||Pii|| 2010 || G || <ref><pubmed>20826779</pubmed></ref>
|-
| [[ジアシルグリセロール]] (DAG) ||Daglas, DIGDA|| 2006, 2008 || G || <ref name=ref18685081 /> <ref name=ref20 />
|-
|rowspan="6" | タンパク質相互作用 || [[アクチン]] || ||2004, 2008 || C || <ref name=ref10 /> <ref name=ref18512154><pubmed>18512154</pubmed></ref>
|-
| [[3-ホスホイノシチド依存性プロテインキナーゼ1]]([[phosphoinositide-dependent protein kinase 1]], [[PDK1]])-[[タンパク質キナーゼB]] ([[protein kinase B]], [[PKB]], [[Akt]])相互作用 || ||2007 || B || <ref name=ref17407381 />
|-
| [[タンパク質チロシン脱リン酸化酵素1B]] ([[protein tyrosine phosphatase 1B]], [[PTP 1B]])-[[受容体型チロシンキナーゼ]] ([[receptor tyrosine kinase]]s, [[RTK]]s)相互作用 || || 2002 || B || <ref><pubmed>11872838</pubmed></ref>
|-
| [[乳癌耐性タンパク質]] ([[breast cancer resistance protein]], [[BCRP]])/[[ATP結合カセット輸送体]] ([[ATP-binding cassette sub-family G member]], [[ABCG]])相互作用 || ||2010 || B || <ref><pubmed>20622991</pubmed></ref>
|-
| [[コフィリン]]-[[アクチン]]相互作用 || ||2008 || B || <ref><pubmed>17993279</pubmed></ref>
|-
| [[第10染色体ホスファターゼ・テンシン・ホモログ]] ([[Phosphatase and tensin homolog deleted from chromosome 10]], [[PTEN]])-[[ミオシンV]]相互作用 || ||2009 || B || <ref><pubmed>19767745</pubmed></ref>
|-
|rowspan="8" | [[プロテアーゼ]] || [[カスパーゼ-3]] ||EGFP-DEVD-EBFP|| 1998 || A || <ref name=ref6 />
|-
| [[カスパーゼ-8]] ||CFP-c3-YFP-c6-mRFP|| 2002 || A || <ref name=ref7 />
|-
| [[カスパーゼ-9]] ||SCAT9|| 2011 || A || <ref name=ref8 />
|-
| [[カスパーゼ-7]] ||VDEVDc|| 2006 || A || <ref name=ref9 />
|-
| [[マトリックスメタロプロテアーゼ]] ([[MMP]]) ||YFP-MSS-CFP<sup>display</sup>, MTI-MMP-FRET biosensor|| 2007, 2008 || A || <ref><pubmed>17187878</pubmed></ref><ref><pubmed> 18441011</pubmed></ref>
|-
| [[wj:第Xa因子|第Xa因子]] || ||1996 || A || <ref name=ref5 />
|-
|[[カルパイン]]活性||pYSCS|| 2000 || A || <ref><pubmed>10688895</pubmed></ref>
|-
| [[プレセニリン]] ||GFP-PSI-RFP|| 2009 || A || <ref><pubmed>19924286</pubmed></ref>
|-
|rowspan="5" | その他 ||細胞膜張力センサー ||stFRET|| 2008 || D || <ref><pubmed>18479457</pubmed></ref>
|-
| [[膜電位]] ||VSFP, Mermaid, ArcLight, VSFP-Butterfly|| 2001, 2008, 2012 || D || <ref><pubmed>11454036</pubmed></ref> <ref name=ref15 /> <ref><pubmed> 22958819</pubmed></ref> <ref><pubmed> 23868559</pubmed></ref>
|-
| [[ミオシンII]] ||GSldCB|| 1998, 2006 || D || <ref><pubmed>9845076</pubmed></ref><ref><pubmed> 16939200</pubmed></ref>
|-
| [[wj:ヒト免疫不全ウイルス|ヒト免疫不全ウイルス]]Revタンパク質 ||YRGnC-11ad|| 2005 || E || <ref><pubmed>16013840</pubmed></ref>
|-
|| [[wj:酸化還元|酸化還元]] ||Redoxfluor, Gaskins|| 2010, 2011 || D || <ref><pubmed>20498274</pubmed></ref><ref><pubmed> 21606117</pubmed></ref>
|}
プローブデザインA-Gは図4に対応している。京都大学医学部 松田道行による[http://www.lif.kyoto-u.ac.jp/labs/fret/phogemon/index.htm Phogemon Project] などを参考に作成。
==蛍光色素の選択==
===GFPとその関連タンパク質===
現在多くの場合GFPあるいはその関連タンパク質が用いられている。
蛍光強度比イメージングの場合は、GFPの色彩変異体であるシアン色蛍光タンパク質CFPと黄色蛍光タンパク質YFPのFRETペアがよく用いられている。CFPの中でも、Ceruleanが明るい蛍光を示すためこれを用いるべきである。YFPの変異体の中では、Venus、Ypetがよい。いずれも若干の凝集傾向が有り、これはタンパク質表面にある三つのアラニン残基のメチル基によるものとされており、それを変異させたmonomeric GFP (A206K変異体)で凝集を避ける事が出来る<ref name=ref11988576><pubmed>11988576</pubmed></ref> <ref name=ref18512154 />。一方で、プロテアーゼプローブなどでは、FRETダイナミックレンジが改善するという報告もある<ref name=ref15696158><pubmed>15696158</pubmed></ref>
<ref name=ref17586775><pubmed>17586775</pubmed></ref>。CFPとYFPはいずれもGFPの変異体で殆ど同一の配列である為か、トランスジェニック動物が作りにくい事が経験的に知られている{kamioka, 2012}。
近年、Clover(緑色域)とmRuby2(赤色域)がより良いFRETペアであると報告されている<ref><pubmed>22961245</pubmed></ref>。
一方、蛍光寿命イメージングとしてはドナーとしてmGFP、アクセプターとしてmRFPもしくはmCherryが用いられる。この場合、アクセプターの蛍光強度は問題ではないので蛍光を発しないREACh, darkVenus, superREAChなども用いられる<ref name=ref16537489><pubmed>16537489</pubmed></ref><ref name=ref18512154 /> <ref name=ref18302935><pubmed>18302935</pubmed></ref>。
これらのプローブはどうしてもある程度細胞内に過剰発現する事になる為、それ自体が細胞機能に影響を与える事が有る。そのため、観察したい細胞機能が影響受けていないかは厳密に限局すべきである。
また、[[シナプス]]や[[樹状突起棘]]といった微小な構造を観察する際にはプローブの拡散が問題になる。FRETが変化した空間分布が、FRETで観察している分子の空間分布を見ているのか、あるいは変化を受けたプローブ自体が拡散しているのかを区別する必要がある。予め[[光活性化GFP]]を用い、プローブの拡散速度を求めておくのが一つの方法である。
===Immuno FRET===
一方、GFPの代わりに通常の抗原抗体反応を行い、FRETを検出する方法もこころみられており、immuno FRETと呼ばれている。観察したい二つのタンパク質の[[蛍光免疫染色]]を行い、ドナーとアクセプターとなる蛍光ラベルした[[二次抗体]]を用い検出する。その上で、アクセプター褪色法、蛍光強度比イメージングや蛍光寿命イメージングを用いてFRETを検出する。GFPなどで蛍光ラベルしたタンパク質を導入する事無く、内在のタンパク質を検出できる事が特徴であるため、過剰発現の影響が避けられる。
ところが通常用いられる蛍光色素では5-10 nm程度の範囲まででFRETが観察されるのに対し、抗体自体が15 nmの大きさを持っている。また抗体のヒンジ部分で自由に折れ曲がる事が可能である。しかも2個の抗体を用いる。これらを考慮に入れると、目的とする分子の構造変化や相互作用が起こっていてもFRETが検出できない可能性がある。逆に仮にFRETが起きたとしても目的とするタンパク質が本当に相互作用しているかの実証とはならない。確実に言えるのは二つの抗原部位が数十nm以内に存在するという事実だけである。その為、タンパク質の構造変化を見るような実験には用いるのは難しい。また、免疫染色である為、固定したサンプルを用いなければならない。
しかし、最近intrabody、nanobody、FingRなどと呼ばれる希望するタンパク質と特異的に結合する小型のタンパク質配列をデザインする方法が開発されつつある<ref name=ref23836932 ><pubmed> 23836932 </pubmed></ref><ref name=ref23791193><pubmed> 23791193 </pubmed></ref><ref name=ref24005308 ><pubmed> 24005308 </pubmed></ref><ref name=ref16053141 ><pubmed> 16053141 </pubmed></ref>。これを用いると、任意の分子に結合する、抗体よりも小型で、かつ遺伝子によってコードされる蛍光ラベルが可能となるであろう。このような方法を用いる事により、GFP融合タンパクによらない、内在性のタンパク質の相互作用を検出できる可能性がある。
==神経科学分野への応用例 ==
1997年、宮脇らによって、CFPおよびYFPを利用した、細胞内[[カルシウム]] プローブ、カメレオンが開発され<ref name=ref16 />、さらに、cAMP<ref><pubmed>10620803</pubmed></ref>, cGMP<ref name=ref11140757 />、リン酸化<ref name=ref19 />を初めとした主要な細胞内シグナル伝達分子のFRETプローブが次々と作製され、分子のリアルタイムな活性および局在の活性の解明に大きく貢献した。
2000年初期に記憶の形成に必須なシグナル分子、Ca<sup>2+</sup>/カルモデュリン依存性タンパク質キナーゼII (CaMKII)の活性化を評価するためのFRETプローブ、 Camuiが開発された<ref name=ref11 />。CaMKIIはそれまでは、一旦活性化されたらその活性が自己リン酸化により持続する事で、長期に亘る記憶に必要なシナプス反応の増強を維持すると考えられてきたが、実際にはCaMKIIの活性化は一過性である事が示された<ref name=ref19295602 />。
一方、[[樹状突起]][[スパイン]])の形態を制御する[[アクチン]]の重合を可視化するためのFRETプローブが開発され、アクチンの重合が長期増強現象に伴い引き起こされる事、またそれが長期間維持される事が示された<ref name=ref10 />。その調節の上流にある[[Rho族低分子量Gタンパク質]][[Cdc42]]、[[RhoA]]の活性も同様に維持される事が判った<ref name=ref19295602 /> <ref><pubmed>18556515</pubmed></ref> <ref name=ref21423166 />。
個体においてもFRET測定法が導入されている。神経回路ネットワークにおける[[シナプス]]の役割を解明する目的で、[[フェレット]]の[[大脳皮質]][[視覚野]]にCaMKIIプローブを発現し、[[片眼剥奪]]によって、神経回路ネットワークに変化を起こした時のCaMKIIの活性化の変化を観測している<ref><pubmed>22160721</pubmed></ref>。また、神経活動をモニターする膜電位プローブを開発し[[マウス]]の[[洞毛]](ヒゲ)刺激の投射先である[[体性感覚野]][[バレル皮質]]での入力特異的な神経の活性化を観察している<ref><pubmed>20622860</pubmed></ref>。
病態との関係では、神経細胞内のカルシウム濃度を測定するために、[[オレゴングリーンBAPTA]]の蛍光寿命の変化から、カルシウム濃度を測定し、[[アストロサイト]]でのカルシウム濃度が、[[アルツハイマー病]]モデル[[マウス]]と正常マウスで異なることが報告されている<ref><pubmed>19251629</pubmed></ref>。
Homo-FRETも応用されている。CaMKIIは12量体を形成しているが、異方性の変化を基に、その構造中に二量体の単位が存在し、活性化に伴う二量体同士の位置関係が変化することが明らかにされている<ref><pubmed>19339497</pubmed></ref>。
== 将来展望 ==
== 将来展望 ==
脳研究は、生動物の脳の神経細胞の活動を、広範囲で、より深部で観察したり、逆に神経細胞内の超微細構造を観察する方向に移るであろう。現在、FRETを基にした''in vivo''イメージングは、応答の低さ、蛍光の弱さなどの難点はあるものの、蛍光タンパク質の蛍光強度や顕微鏡の性能の改良は日進月歩であり改善されていくであろう。また、神経活動に必要なシグナル伝達を同時に観察するために、マルチカラーイメージングの試みもなされるであろう。その際には、2つの波長を必要とする蛍光強度比変化を基にするFRET測定よりも、蛍光寿命イメージングが適している。
==外部リンク==
脳研究は、生きたままの状態の脳の神経細胞の活動を、広範囲で、より深部で観察したり、逆に神経細胞内の超微細構造を観察する方向に移るであろう。現在、FRETを基にしたin vivoイメージングは、応答の低さ、蛍光の弱さなどの難点はあるものの、蛍光タンパク質の蛍光強度や顕微鏡の性能の改良は日進月歩であり改善されていくであろう。また、神経活動に必要なシグナル伝達を同時に観察するために、マルチカラーイメージングの試みもなされるであろう。その際には、2つの波長を必要とする蛍光強度比変化を基にするFRET測定よりも、蛍光寿命を観察するFLIM測定が適している。
*[http://www.lif.kyoto-u.ac.jp/labs/fret/phogemon/index.htm Phogemon Project] 京都大学医学部 松田道行よるFRETセンサー開発とイメージング方法の解説。文字化けする時にはブラウザーの設定をShift-JISにするよい。
*[http://www.lif.kyoto-u.ac.jp/labs/fret/e-phogemon/index.htm Phogemon Project] 同英語版 。
<br>
== 参考文献 ==
== 参考文献 ==
<references />
<references />
フェルスター共鳴エネルギー移動(FRET) 英:Förster resonance energy transfer 英略称:FRET、独:仏:
[ 1]
図1:ヤブロンスキーダイヤグラム 図2:励起光によって励起された光子が基底状態に戻る際の減衰曲線 図3:Donorの蛍光スペクトルとAcceptorの励起スペクトルに重なりがあるときに、FRETが起きる。例としてAcceptorをGFP、DonorをRFPで表している。 原理 図1のヤブロンスキーダイヤグラムのように、Donorの蛍光団の電子が、励起光により基底状態から励起状態に励起される。励起された電子は、回転エネルギーや振動エネルギーを失いながら、励起状態の底まで行き着く。その後、基底状態に戻る際に、蛍光としてエネルギーを放出する。蛍光の減衰曲線は、速度定数を
k
{\displaystyle k\ }
k
f
{\displaystyle k_{f}\ }
k
−
k
f
{\displaystyle k-k_{f}\ }
k
f
{\displaystyle k_{f}\ }
k
f
(
r
,
κ
)
=
k
D
Q
D
κ
2
r
6
(
9000
(
I
n
10
)
128
π
5
N
n
4
)
∫
0
∞
F
D
(
λ
)
ϵ
A
(
λ
)
λ
4
d
λ
{\displaystyle k_{f}(r,\kappa )={\frac {k_{D}Q_{D}\kappa ^{2}}{r^{6}}}\left({\frac {9000(In10)}{128\pi ^{5}Nn^{4}}}\right)\int _{0}^{\infty }F_{D}(\lambda )\epsilon _{A}(\lambda )\lambda ^{4}\,d\lambda }
k
D
{\displaystyle k_{D}\ }
Q
D
{\displaystyle Q_{D}\ }
κ
{\displaystyle \kappa \ }
r
{\displaystyle r\ }
N
{\displaystyle N\ }
n
{\displaystyle n\ }
F
D
{\displaystyle F_{D}\ }
ϵ
A
{\displaystyle \epsilon _{A}\ }
r
{\displaystyle r\ }
κ
2
{\displaystyle \kappa ^{2}\ }
2
3
{\displaystyle {\tfrac {2}{3}}\ }
検出
ドナーとアクセプターの蛍光強度を測定する方法 FRETが起きると、Donorの蛍光強度が減少し、Acceptorの蛍光強度が増加する。測定の際には蛍光強度の変化を測定することになるが、細胞などの試料においては、細胞の形状変化に伴う蛍光強度変化などが起きることから、実際にはドナーとアクセプターの蛍光強度のの変化を取得することによって、これらのファクターを除外する。
ドナーの蛍光寿命を測定する方法 近年、時間相関単一光子計数法とpulsing laserの相性の良さから、時間分解能の向上により、蛍光寿命を比較的短時間で取得することが可能となった。 蛍光寿命は、GFPおよびそのcolor variantタンパクでは、1-5 nsec、希土類錯体などは、1µsec、pyren coronenなどは、400, 200 nsecである。上述のように、FRETが起きると蛍光寿命を表す減衰曲線の傾きが変わる。これを基にFRETを観察する。
Anisotropyを測定する方法 一つの蛍光団のストークスシフトが小さい場合、励起スペクトルと蛍光スペクトルの重なりが大きい。このような蛍光団では、同一の蛍光団同士で、Homo-FRETが生じる。Homo-FRETは、蛍光強度および蛍光寿命は変化しないが、異方性が変わる。この原理を用いて、一般的には、分子同士のクラスターの度合いなどに応用されている。
神経科学分野への応用 [ 2] [ 3] [ 4] [ 5] [ 6] [ 7] [ 8] [ 9] [ 10]
Homo-FRETも応用されている。CaMKIIは12量体を形成しているが、異方性の変化を基に、その構造中にdimerの単位が存在し、活性化に伴うdimer同士の位置関係が変化することをvogelらが明らかにしている[ 11]
将来展望 脳研究は、生きたままの状態の脳の神経細胞の活動を、広範囲で、より深部で観察したり、逆に神経細胞内の超微細構造を観察する方向に移るであろう。現在、FRETを基にしたin vivoイメージングは、応答の低さ、蛍光の弱さなどの難点はあるものの、蛍光タンパク質の蛍光強度や顕微鏡の性能の改良は日進月歩であり改善されていくであろう。また、神経活動に必要なシグナル伝達を同時に観察するために、マルチカラーイメージングの試みもなされるであろう。その際には、2つの波長を必要とする蛍光強度比変化を基にするFRET測定よりも、蛍光寿命を観察するFLIM測定が適している。
参考文献
↑
Förster, T. (2012). Journal of biomedical optics , 17(1), 011002.
[PubMed:22352636 ]
[WorldCat ]
[DOI ]
↑
Miyawaki, A., Llopis, J., Heim, R., McCaffery, J.M., Adams, J.A., Ikura, M., & Tsien, R.Y. (1997). Nature , 388(6645), 882-7.
[PubMed:9278050 ]
[WorldCat ]
[DOI ]
↑
Sato, M., Hida, N., Ozawa, T., & Umezawa, Y. (2000). Analytical chemistry , 72(24), 5918-24.
[PubMed:11140757 ]
[WorldCat ]
[DOI ]
↑
Takao, K., Okamoto, K., Nakagawa, T., Neve, R.L., Nagai, T., Miyawaki, A., ..., & Hayashi, Y. (2005). The Journal of neuroscience : the official journal of the Society for Neuroscience , 25(12), 3107-12.
[PubMed:15788767 ]
[PMC ]
[WorldCat ]
[DOI ]
↑
Okamoto, K., Nagai, T., Miyawaki, A., & Hayashi, Y. (2004). Nature neuroscience , 7(10), 1104-12.
[PubMed:15361876 ]
[WorldCat ]
[DOI ]
↑
Lee, S.J., Escobedo-Lozoya, Y., Szatmari, E.M., & Yasuda, R. (2009). Nature , 458(7236), 299-304.
[PubMed:19295602 ]
[PMC ]
[WorldCat ]
[DOI ]
↑
Harvey, C.D., Yasuda, R., Zhong, H., & Svoboda, K. (2008). Science (New York, N.Y.) , 321(5885), 136-40.
[PubMed:18556515 ]
[PMC ]
[WorldCat ]
[DOI ]
↑
Murakoshi, H., Wang, H., & Yasuda, R. (2011). Nature , 472(7341), 100-4.
[PubMed:21423166 ]
[PMC ]
[WorldCat ]
[DOI ]
↑
Mower, A.F., Kwok, S., Yu, H., Majewska, A.K., Okamoto, K., Hayashi, Y., & Sur, M. (2011). Proceedings of the National Academy of Sciences of the United States of America , 108(52), 21241-6.
[PubMed:22160721 ]
[PMC ]
[WorldCat ]
[DOI ]
↑
Kuchibhotla, K.V., Lattarulo, C.R., Hyman, B.T., & Bacskai, B.J. (2009). Science (New York, N.Y.) , 323(5918), 1211-5.
[PubMed:19251629 ]
[PMC ]
[WorldCat ]
[DOI ]
↑
Thaler, C., Koushik, S.V., Puhl, H.L., Blank, P.S., & Vogel, S.S. (2009). Proceedings of the National Academy of Sciences of the United States of America , 106(15), 6369-74.
[PubMed:19339497 ]
[PMC ]
[WorldCat ]
[DOI ]