「ドリフト拡散モデル」の版間の差分
Kentaro Katahira (トーク | 投稿記録) 細 →モデルの定式化 |
|||
| (2人の利用者による、間の58版が非表示) | |||
| 1行目: | 1行目: | ||
<div align="right"> | <div align="right"> | ||
<font size="+1">[https://researchmap.jp/7000006268 片平 健太郎]</font><br> | <font size="+1">[https://researchmap.jp/7000006268 片平 健太郎]</font><br> | ||
'' | ''国立研究開発法人 産業技術総合研究所 人間情報インタラクション研究部門''<br> | ||
<font size="+1">[https://researchmap.jp/ykunisato 国里 愛彦]</font><br> | <font size="+1">[https://researchmap.jp/ykunisato 国里 愛彦]</font><br> | ||
'' | ''専修大学 人間科学部心理学科''<br> | ||
</div> | </div> | ||
英語名:drift diffusion model | |||
類義語:逐次サンプリングモデル (sequential sampling model) | 類義語:逐次サンプリングモデル (sequential sampling model) | ||
{{box|text= | {{box|text= | ||
ドリフト拡散モデルは,刺激呈示から反応が起こるまでの意思決定プロセスを説明する数理モデルの一つである。反応選択と反応時間の分布を説明するモデルとして,心理学や神経科学の研究において幅広く用いられている。その性質は確率過程に関する数学的理論や計算機シミュレーションにより詳細に調べられている。実際の反応データからモデルのパラメータを推定することも可能であり,パラメータの個人差や群間差を定量化することにも用いられている。また,モデルの振る舞いに類似する神経活動も観測されており,意思決定の神経基盤のモデルとしても注目されている。 | |||
}} | }} | ||
== | ==ドリフト拡散モデルの概要== | ||
[[Image:DDMの概要.png|thumb|420px|<b>図1.ドリフト拡散モデルにおける反応と反応時間の生成過程</b>]] | |||
ドリフト拡散モデルは,刺激呈示から反応が起こるまでの経過時間(反応時間)と反応選択の分布を説明するモデルである。ドリフト拡散モデルは,Ratcliff | |||
<ref name=Ratclif1978><b>Ratcliff, R.(1978).</b><br>A theory of memory retrieval.<br><i>Psychological Review</i> 1978, 85(2);59–108</ref>により提案され,心理学や神経科学における反応時間のモデリングにおいて,幅広く用いられている<ref name=Ratclif2016><pubmed> 26952739 </pubmed></ref>。 | |||
ドリフト拡散モデルが適用されるのは,刺激の呈示後から1秒から2秒程度の時間内に二種類の反応から一つを選択することが求められるようなタイプの意思決定である。熟考の末判断を下すような時間のかかる意思決定は適用対象ではないとされる。また,いずれかの反応が正解であり,もう片方の反応は不正解とされる場合が多いが,必ずしもその限りではない。適用される意思決定のタイプとしては,呈示された刺激が以前にも呈示されたものであるか新規なものであるかを判断する記憶課題<ref name=Ratclif1978 />,明るさや動きなどの刺激の物理的特徴について判断する知覚的判断<ref><pubmed> 12812276</pubmed></ref><ref><pubmed>15066392</pubmed></ref>,その他,語彙判断<ref><pubmed>14756592</pubmed></ref>,数量的判断<ref><pubmed>24446719</pubmed></ref>,文章処理<ref><pubmed>20431690</pubmed></ref>,選好判断<ref><pubmed>20835253</pubmed></ref>など多岐にわたる。 | |||
ドリフト拡散モデルは,逐次サンプリングモデル (sequential sampling model) の一種である。逐次サンプリングモデルでは,刺激が呈示されると生体は時間経過とともに確率的に情報を蓄積していき,その蓄積が境界を越えた時に反応が出力されると仮定する。図1に示すように,行動課題を実施した際に,反応までにかかる時間は,(1)刺激の読み込み,(2)エビデンス(判断を下すのに必要な情報)の蓄積,(3)反応 (ボタン押しなどの運動) に分解することができる。(1)刺激の読み込みと(3)反応は,判断に関わる過程ではないので,非決定時間 (non decision time) と呼ばれる。(2)エビデンスの蓄積は,決定時間 (decision time) と呼ばれる。ドリフト拡散モデルをはじめとする逐次サンプリングモデルを用いることで,非決定時間の推定と決定時間の生成に関わるパラメータの推定を行うことができる。 | |||
ドリフト拡散モデルにおけるエビデンスの蓄積過程は,開始点<math>z</math>から始まり,一定のドリフト率に従ってエビデンスが蓄積される (図1)。そして,上下いずれかの境界までエビデンスが蓄積されると反応が出力される。図1の場合,上側の境界<math>a</math>に到達すると反応Aが出力され,下側の境界0に到達すると反応Bが出力される。開始点と境界<math>a</math>の距離が長いほど,エビデンスの蓄積にかかる時間が長くなる。また,開始点から境界までの蓄積過程における速度は,ドリフト率に依存する。ドリフト率が大きいほど,境界まで到達する時間は短くなる。開始点,ドリフト率,境界,そして非決定時間がドリフト拡散モデルの振る舞いを決定する主なパラメータである。 | |||
これらのパラメータの値には個人差 (個体差) | これらのパラメータの値には個人差 (個体差) があると考えられ,また,個人の中でも状態や実験条件などによって変化すると仮定される。例えば,生体が注意深く反応するほど境界パラメータ<math>a</math>は大きくなり,開始点と境界の間は広がると仮定される。逆に,素早い反応が求められる場合は<math>a</math>は小さくなると仮定される。一般に,意思決定におけるスピードと正確性の間には,片方を重視するともう片方が損なわれるというトレードオフがある。境界パラメータ<math>a</math>の変化を通して,ドリフト拡散モデルにもそのようなスピードと正確性のトレードオフが生じる。開始点パラメータ<math>z</math>は刺激に関する事前の期待に対応する。例えば,反応Aを起こすべき刺激の出現が期待される場合は,開始点パラメータは大きい (<math>a</math>に近い) 値をとるとされる。 | ||
==モデルの定式化== | ==モデルの定式化== | ||
[[Image:DDM_animation.gif|thumb|320px|<b>図2.ドリフト拡散モデルのエビデンス蓄積過程と,反応時間分布。</b>ドリフト率や開始点,境界は試行間で固定している (<math>v = 1, z = 0.5, a = 1</math> )。]] | |||
ここでは,反応Aと反応Bのいずれかの反応が求められる強制二肢選択課題を想定し,基本的なドリフト拡散モデルを考える。上側の境界を<math>a</math>,下側の境界を0, 開始点を<math>z</math>とする。上側の境界に決定変数 (decision variable) <math>x</math>が到達した場合,そのタイミングで反応Aが起こり,下側の境界である0に到達したらそのタイミングで反応Bが起こると仮定する。刺激が呈示されてから,刺激情報の読み込みや反応の準備に必要な時間が経過してからエビデンスの蓄積が開始され,<math>x</math>が変化する。エビデンスの蓄積過程は以下の式のように連続時間上で定義される確率過程である,ウィーナー過程 (ブラウン運動) に従うとする。 | |||
<math>dx = v dt + \sigma dW</math> | |||
ここで,<math>dx</math> は微小な時間間隔 <math>dt</math>の間の<math>x</math>の変化を表す。<math>v</math>はドリフト率である。反応Aが正解である場合は<math>v > 0</math>,反応Bが正解である場合は<math>v < 0</math>とする。<math>\sigma dW</math>は平均が0で分散が<math>\sigma^2 dt</math>となる正規分布に従うホワイトノイズを表す。ウィーナー過程は連続時間上で定義されるが,計算機上でシミュレーションする場合は,離散時間で近似する必要がある。ここでは理解が容易なシンプルな近似法を考える。微小な時間幅<math>\Delta t</math>を考え,平均0, 分散1の標準正規分布に従う正規乱数<math> \epsilon</math>を用いて,この時間幅<math>\Delta t</math>あたりの変数<math>x</math>の変化量を,以下の式で設定する。 | |||
<math>\Delta x = v \Delta t + \sigma \epsilon \sqrt{\Delta t} </math> | |||
この式で<math>x</math>を更新していくことによりエビデンスの蓄積過程をシミュレートできる。図2の各軌道はこの計算により得られたものである。 | |||
標準的なドリフト拡散モデルでは,開始点とドリフト率,および非決定時間は,試行間で変動すると仮定される<ref name=Ratclif1978 />。ドリフト率の試行間変動は,刺激に対する注意の変動などに対応すると考えられ,標準偏差<math>\eta</math>の正規分布に従って変動すると仮定される。この変動を仮定することで,正反応より誤反応の方が反応時間が長くなるということが説明可能となる。これは,ドリフト率が小さくなる試行において,誤反応が起こりやすくなり,かつ反応時間が長くなるためである。開始点の試行間変動は区間<math>[z-s_{z}, z+s_{z}]</math>の一様分布に従うと仮定される。これは,ある特定の刺激がどの程度呈示されやすいかについての期待が試行間で変動することを表現する。この変動により,誤反応が起こる試行で反応時間が短くなることが説明できる。これは,開始点が誤反応側の境界に寄っているときに,早い時間帯で誤反応が起きやすくなるためである。また,非決定時間も区間<math>[T_{er}-s_{t}, T_{er}+s_{t}]</math>の一様分布に従うと仮定される。 | |||
したがって,標準的なドリフト拡散モデルのパラメータは,開始点の平均 (<math>z</math>),開始点の試行間変動 (<math>s_{z}</math>),ドリフト率の平均 (<math>v</math>),ドリフト率の標準偏差 (<math>\eta</math>),境界 (<math>a</math>),非決定時間の平均 (<math>T_{er}</math>),非決定時間の試行間変動 (<math>s_{t}</math>) の7つとなる。 | |||
==反応時間分布および選択確率の解析解== | |||
二つの選択に関する上記のモデルにおいて,各パラメータを固定した場合 (試行間変動は仮定しない場合),それぞれの選択肢を選ぶ確率,およびその反応時間の分布は次のように解析的に導出される <ref name=Ratclif1978 />。下側の境界 (0) に到達し,反応Bが起こる確率は, | |||
<math>\frac{e^{-2va/\sigma^2}-e^{-2vz/\sigma^2}}{e^{-2va/\sigma^2}-1}</math> | |||
となる。ただしドリフト率<math>v</math>が0だった場合はこの確率は | |||
<math>1-z/a</math> | |||
となる。さらに,反応Bが起こり,かつ (非決定時間を除いた) その反応時間が<math>t </math>となる条件付きの確率密度は | |||
<math>\frac{\pi \sigma^2}{a^2} e^{-zv/\sigma^2} \sum_{k=1}^\infty k \sin \left(\frac{\pi z k}{a}\right) e^{-\frac{1}{2} (v^2 / \sigma^2 + \pi^2 k^2 \sigma^2/a^2)t} </math> | |||
で与えられる。境界<math>a</math> | で与えられる。境界<math>a</math>に到達し反応Aが起こり,かつその反応時間が<math>t</math>となる確率密度は,上の式において<math>v</math>を<math>-v</math>で, <math>z</math> を<math>a -z</math>で置き換えることで得られる。図2の上下の曲線はこれらの式により得られた条件付きの確率密度関数である。シミュレーションにより得た反応時間のヒストグラムもサンプルが増えるにつれてこの分布に近づいていくことがわかる。 | ||
==モデルフィッティング== | ==モデルフィッティング== | ||
上記のように解析的に得られる反応時間の分布が実際のデータに近づくようにパラメータを調整することで,明示的にドリフト拡散過程をシミュレートせずともモデルのパラメータを推定することができる。また,複数ある候補のモデルからデータをよりよく説明するモデルを選択することも可能となる。パラメータの推定やモデル選択をする作業を総称してモデルフィッティングと呼ぶ。 | |||
実験で収集された反応データに対して,モデルフィッティングをする方法として,<math>\chi^{2}</math>最小化,最尤法,重み付き最小二乗法,ベイズ推定等がある<ref><pubmed> 12412886</pubmed></ref>。モデルフィッティング用のソフトウェアとしては,以下がある。 | |||
* Fast-dm<ref><pubmed>18183889</pubmed></ref>: Voss & Voss (2007)が開発したWindowsで動作するソフトウェア。最尤推定,Kolmogorov-Smirnov,<math>\chi^{2}</math>最小化などの方法が可能である。 | |||
* DMAT<ref><pubmed>18411528</pubmed></ref>: Vandekerckhove & Tuerlinckx (2008)が開発した,ドリフト拡散モデル用MATLABツールボックス。 | |||
* EZ2<ref><pubmed>17546727</pubmed></ref>: Wagenmakers, Van Der Maas, & Grasman(2007)によって提案されたドリフト拡散モデルから試行間変動の推定を除いたシンプルなEZ拡散モデルを用いてモデルフィッティングするRパッケージ。 | |||
* HDDM<ref><pubmed>23935581</pubmed></ref>: Wiecki, Sofer, & Frank(2013)が開発した,ドリフト拡散モデルを階層ベイズ推定するPythonパッケージ。 | |||
* hBayesDM<ref><pubmed>29601060</pubmed></ref>: Ahn, Haines, & Zhang(2017)が開発した,意思決定課題に対して階層ベイズモデリングを行うRパッケージ。 | |||
* rtdists(https://github.com/rtdists/rtdists/): ドリフト拡散モデルをはじめとする反応時間のモデリングに有用な関数が含められたRパッケージ。 | |||
それぞれのモデルや推定方法には仮定がおかれていることがあり,モデルフィッティングに用いるデータがその仮定に合っているかどうかは事前に確認する必要がある。各種推定法に関する専門家による推奨については,Boehmらの論文<ref name=Boehm2018><b>Boehm, U., Annis, J., Frank, M. J., Hawkins, G. E., Heathcote, A., Kellen, D., Krypotos, A.-M., Lerche, V., Logan, G. D., Palmeri, T. J., van Ravenzwaaij, D., Servant, M., Singmann, H., Starns, J. J., Voss, A., Wiecki, T. V., Matzke, D., & Wagenmakers, E.-J.(2018). </b><br>Estimating across-trial variability parameters of the Diffusion Decision Model: Expert advice and recommendations.<br><i>Journal of Mathematical Psychology</i>, 87, 46–75</ref>にまとめられている。また,ドリフト拡散モデルでのモデルフィッティングにあたっては,十分なデータ数が必要になる。特に反応時間の分布の情報を用いてパラメータ推定する方法の場合は,試行数が100程度の場合は,ドリフト拡散モデルの試行間変動性にかかわるパラメータの推定が真値からずれることが示されている<ref><pubmed>18229471</pubmed></ref>。そのため,試行間変動性にかかわるパラメータの推定を行う場合は,できるだけ多くの試行数が必要になるが,試行数を増やすと参加者の動機づけが低下する,疲れの影響が出る,などの問題も生じる。また,そもそも試行数を増やすことが難しい実験状況も多い<ref name=Boehm2018 />。そこで,パラメータ推定にあたり,参加者集団のパタメータの分布も仮定した階層ベイズ推定を行うことで,各参加者の試行数は少なくとも安定した推定する方法も提案されている<ref><pubmed>23935581</pubmed></ref><ref><pubmed>29601060</pubmed></ref>。 | |||
==適用事例== | ==適用事例== | ||
[[Image:DDM_z_vs_v.png|thumb| | [[Image:DDM_z_vs_v.png|thumb|420px|<b>図3.反応時間分布に及ぼすドリフト率 (左) 開始点パラメータ (右) の影響。</b>破線は参照となるベースのモデル (<math>v = 1.0, z = 0.5, a = 1.0</math>) を表す。左のパネルではドリフト率を大きくした場合 (<math>v = 2.0</math>) ,右のパネルでは開始点を高くした場合 (<math>z = 0.7</math>) の結果をそれぞれ実線で表している。]] | ||
ドリフト拡散モデルを用いることで,反応分布の形状の情報を利用することが可能となり,単純な平均反応時間の解析では取りこぼされていた情報を利用して詳細なプロセスを検討することができる。例えば,開始点パラメータ<math>z</math>を増加させることと,ドリフト率<math>v</math>を増加させることはいずれも反応Aの選択確率を増加させ,その平均的な反応時間を短くする効果があるが,その反応時間分布の形状に与える影響が異なる。図3の左のパネルでは,開始点パラメータ<math>z</math>を固定し,ドリフト率を増加させている (実線が増加後)。この場合,反応Aの確率が高くなり,速い反応時間の密度が増加するため平均反応時間は短くなるが,反応時間の分布のピーク (最も密度が高くなる位置) はほとんど変化しない。一方,開始点パラメータ<math>z</math>を<math>a</math>に近づけた場合 (図3右) は,反応Aの反応時間分布のピークが速い時間帯にシフトし,分布の歪みが大きくなっている。 | |||
ヒトやその他の動物の意思決定には,現在の感覚入力や過去の選択の結果のみならず,過去の選択履歴が次の選択に影響することが知られている。同じ選択を繰り返す傾向は選択の慣性 (inertia) や固執性 (perseverance) と呼ばれている<ref><pubmed>24333055</pubmed></ref>。そのような傾向はドリフト拡散モデルではエビデンスの蓄積の開始点にバイアスを与えるという解釈が可能である。しかし,実際の知覚的意思決定課題における選択データにおいては,過去と同じ選択肢が選ばれる効果は,図3左のように比較的反応が遅い場合でも見られ,そのようなデータは開始点よりはむしろドリフト率が過去と同じ選択をする方向にバイアスがかかるとするモデルでよく説明されることが報告されている<ref><pubmed>31264959</pubmed></ref>。この結果は,選択履歴の効果が,知覚的なエビデンスの蓄積過程に影響するということを示唆している。 | |||
ドリフト拡散モデルのパラメータの推定値を利用して,選択に関するプロセスの個人差に影響する要因も検討されている。代表的な事例は加齢の効果について調べたものである。例えば高齢者は一般に多くの認知課題において反応が遅くなることが示されているが,ドリフト拡散モデルを適用して検討した研究では,高齢者の反応には長い非決定時間,そして境界の間隔が大きいという特徴はあるものの,ドリフト率には若年者との違いはないということが報告されている<ref><pubmed>19962693</pubmed></ref>。一方で,幼児では境界分離が大きく,非決定時間が長いことに加え,ドリフト率も比較的小さいことが示されている<ref><pubmed>22188547</pubmed></ref>。また,注意欠如・多動症 (ADHD) や読字障害 (dyslexia) を有する若年者はそうでない統制群に比べ,ドリフト率が低い傾向があることを示した研究もある<ref><pubmed>20926067</pubmed></ref><ref><pubmed>22010894</pubmed></ref>。一般知能 (IQ) との関係に関しては,高IQ群は低IQ群よりドリフト率が2倍程度高いという結果が報告されている <ref><pubmed>19962693</pubmed></ref> <ref><pubmed>21707207</pubmed></ref> 。 | |||
==神経活動との対応== | |||
主にサルを対象とした単一細胞レベルでの神経活動記録により,エビデンスの蓄積過程に対応する神経活動が検討されてきた。例えば視線でターゲットを選択することで反応する意思決定課題においては,ターゲットの方向へのサッケード時に選択的に活動するLIP野 (lateral intraparietal cortex) の細胞は刺激の呈示とともに徐々に活動が増加し,ある閾値に到達したときにサッケード反応が起こるということが観測されており,その振る舞いはエビデンスの蓄積を表現する逐次サンプリングモデルと対応付けられるという議論がある<ref><pubmed>8570606</pubmed></ref>。 | |||
==その他の逐次サンプリングモデル== | ==その他の逐次サンプリングモデル== | ||
[[Image:逐次サンプリングモデルの図.png|thumb|520px|<b> | [[Image:逐次サンプリングモデルの図.png|thumb|520px|<b>図4.逐次サンプリングモデルの種類</b>(Ratcliff et al.,2016<ref name=Ratclif2016 />を元に一部改変)]] | ||
逐次サンプリングモデルは,ドリフト拡散モデルだけではない。図4に示すように,逐次サンプリングモデルは,エビデンスの蓄積に関する基準が絶対的か相対的か,対象とする時間が連続的か離散的か,蓄積するエビデンスが連続的か離散的か,ドリフト率が固定か変化するかなどによって分類することができる。ドリフト拡散モデルは,逐次サンプリングモデルの代表的なモデルであるが,モデルの設定においては複数あるモデルの1つの形式であると言える(代表的な逐次サンプリングモデルのモデル間の差異については,Ratcliff & Smith(2004)<ref><pubmed>15065913</pubmed></ref>を参照)。 | |||
[[Image:LBAの概要.png|thumb|420px|<b>図5.線形弾道蓄積モデルにおける反応と反応時間の生成過程</b>]]<br> | |||
ドリフト拡散モデル以外の代表的な逐次サンプリングモデルとして,線形弾道蓄積モデル<ref><pubmed>18243170</pubmed></ref>がある。図5にあるように,線形弾道蓄積モデルは,ドリフト拡散モデルと類似しているが,エビデンスの蓄積の基準が絶対的なことと確率的ではない点が異なる。ドリフト拡散モデルでは,反応はエビデンス蓄積が上の境界と下の境界のどちらに到達するかで決まる相対的なものであった。一方,線形弾道蓄積モデルでは,それぞれの反応は独立してエビデンスの蓄積を行って,最終的に先に閾値(<math>b</math>)に到達した反応が出力される(図5の場合,先に<math>b</math>に到達した反応Aが出力される)。エビデンスの蓄積が始まる点を開始点(<math>a</math>)と呼び,選択肢で同一のこともあるが,異なることもある。開始点の位置の違いは,エビデンスの蓄積の前に存在する選択肢に対するバイアスとして解釈される。ドリフト拡散モデルと同様にエビデンスの蓄積の速さはドリフト率(<math>d</math>)が決めるが,蓄積過程は線形かつ非確率的である。各試行のドリフト率(<math>d</math>)は,平均<math>v</math>,標準偏差<math>s</math>の正規分布に従い,各試行の開始点(<math>a</math>)は,0から<math>A</math>(開始点の上限)の一様分布に従う。決定時間は,<math>(b-a)/d</math>で求めることができ,非決定時間 (<math>\tau</math>)は,全試行で一定とする。<math>a</math>と<math>d</math>は,推定するパラメータではなく,<math>v, b, A, s, \tau</math>が推定するパラメータになる。線形弾道蓄積モデルは,ドリフト拡散モデルよりも推定するパラメータが少なく,2選択肢以外の状況にも適用できるので,ドリフト拡散モデルと合わせて今後の活用が期待できる。 | |||
==モデルの拡張 (強化学習モデルとの統合)== | |||
ドリフト拡散モデルは試行内の刺激呈示から反応出力 (選択) までのプロセスを表現するモデルであるが,試行間の選択傾向の変化を表す他の数理モデルと組み合わせることもできる。例えば,報酬に基づく学習のプロセスを表現する代表的なモデルである強化学習モデルと組み合わせた枠組みが提案されている<ref><pubmed>27966103</pubmed></ref><ref><pubmed>25589744</pubmed></ref>。一般の強化学習モデルでは,行動の結果与えられる報酬に基づいて各行動の価値が計算され,価値の高い行動が高い確率で選択される。ドリフト拡散モデルのドリフト率をこの行動価値の関数にすることで,選択肢の価値の差が小さいほど反応が競合し,反応時間が長くなるという効果を表すことができる。そのように強化学習モデルを用いることで,ドリフト拡散モデルによる反応時間や選択の予測が改善できる。また,逆にドリフト拡散モデルにより反応時間の情報を用いることで,強化学習のパラメータの信頼性も改善される <ref><pubmed>30759077</pubmed></ref>。このように選択傾向の変化と反応時間を同時にモデル化して行動の背後にあるプロセスを探るというアプローチは,実験的に観測される情報をフルに活用できる枠組みとしてさらなる発展が期待される。 | |||
==参考文献== | ==参考文献== | ||
<references /> | <references /> | ||
2021年7月2日 (金) 15:35時点における版
英語名:drift diffusion model
類義語:逐次サンプリングモデル (sequential sampling model)
ドリフト拡散モデルは,刺激呈示から反応が起こるまでの意思決定プロセスを説明する数理モデルの一つである。反応選択と反応時間の分布を説明するモデルとして,心理学や神経科学の研究において幅広く用いられている。その性質は確率過程に関する数学的理論や計算機シミュレーションにより詳細に調べられている。実際の反応データからモデルのパラメータを推定することも可能であり,パラメータの個人差や群間差を定量化することにも用いられている。また,モデルの振る舞いに類似する神経活動も観測されており,意思決定の神経基盤のモデルとしても注目されている。
ドリフト拡散モデルの概要
ドリフト拡散モデルは,刺激呈示から反応が起こるまでの経過時間(反応時間)と反応選択の分布を説明するモデルである。ドリフト拡散モデルは,Ratcliff [1]により提案され,心理学や神経科学における反応時間のモデリングにおいて,幅広く用いられている[2]。
ドリフト拡散モデルが適用されるのは,刺激の呈示後から1秒から2秒程度の時間内に二種類の反応から一つを選択することが求められるようなタイプの意思決定である。熟考の末判断を下すような時間のかかる意思決定は適用対象ではないとされる。また,いずれかの反応が正解であり,もう片方の反応は不正解とされる場合が多いが,必ずしもその限りではない。適用される意思決定のタイプとしては,呈示された刺激が以前にも呈示されたものであるか新規なものであるかを判断する記憶課題[1],明るさや動きなどの刺激の物理的特徴について判断する知覚的判断[3][4],その他,語彙判断[5],数量的判断[6],文章処理[7],選好判断[8]など多岐にわたる。
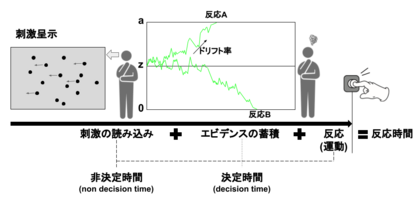
ドリフト拡散モデルは,逐次サンプリングモデル (sequential sampling model) の一種である。逐次サンプリングモデルでは,刺激が呈示されると生体は時間経過とともに確率的に情報を蓄積していき,その蓄積が境界を越えた時に反応が出力されると仮定する。図1に示すように,行動課題を実施した際に,反応までにかかる時間は,(1)刺激の読み込み,(2)エビデンス(判断を下すのに必要な情報)の蓄積,(3)反応 (ボタン押しなどの運動) に分解することができる。(1)刺激の読み込みと(3)反応は,判断に関わる過程ではないので,非決定時間 (non decision time) と呼ばれる。(2)エビデンスの蓄積は,決定時間 (decision time) と呼ばれる。ドリフト拡散モデルをはじめとする逐次サンプリングモデルを用いることで,非決定時間の推定と決定時間の生成に関わるパラメータの推定を行うことができる。
ドリフト拡散モデルにおけるエビデンスの蓄積過程は,開始点から始まり,一定のドリフト率に従ってエビデンスが蓄積される (図1)。そして,上下いずれかの境界までエビデンスが蓄積されると反応が出力される。図1の場合,上側の境界に到達すると反応Aが出力され,下側の境界0に到達すると反応Bが出力される。開始点と境界の距離が長いほど,エビデンスの蓄積にかかる時間が長くなる。また,開始点から境界までの蓄積過程における速度は,ドリフト率に依存する。ドリフト率が大きいほど,境界まで到達する時間は短くなる。開始点,ドリフト率,境界,そして非決定時間がドリフト拡散モデルの振る舞いを決定する主なパラメータである。
これらのパラメータの値には個人差 (個体差) があると考えられ,また,個人の中でも状態や実験条件などによって変化すると仮定される。例えば,生体が注意深く反応するほど境界パラメータは大きくなり,開始点と境界の間は広がると仮定される。逆に,素早い反応が求められる場合はは小さくなると仮定される。一般に,意思決定におけるスピードと正確性の間には,片方を重視するともう片方が損なわれるというトレードオフがある。境界パラメータの変化を通して,ドリフト拡散モデルにもそのようなスピードと正確性のトレードオフが生じる。開始点パラメータは刺激に関する事前の期待に対応する。例えば,反応Aを起こすべき刺激の出現が期待される場合は,開始点パラメータは大きい (に近い) 値をとるとされる。
モデルの定式化

ここでは,反応Aと反応Bのいずれかの反応が求められる強制二肢選択課題を想定し,基本的なドリフト拡散モデルを考える。上側の境界を,下側の境界を0, 開始点をとする。上側の境界に決定変数 (decision variable) が到達した場合,そのタイミングで反応Aが起こり,下側の境界である0に到達したらそのタイミングで反応Bが起こると仮定する。刺激が呈示されてから,刺激情報の読み込みや反応の準備に必要な時間が経過してからエビデンスの蓄積が開始され,が変化する。エビデンスの蓄積過程は以下の式のように連続時間上で定義される確率過程である,ウィーナー過程 (ブラウン運動) に従うとする。
ここで, は微小な時間間隔 の間のの変化を表す。はドリフト率である。反応Aが正解である場合は,反応Bが正解である場合はとする。は平均が0で分散がとなる正規分布に従うホワイトノイズを表す。ウィーナー過程は連続時間上で定義されるが,計算機上でシミュレーションする場合は,離散時間で近似する必要がある。ここでは理解が容易なシンプルな近似法を考える。微小な時間幅を考え,平均0, 分散1の標準正規分布に従う正規乱数を用いて,この時間幅あたりの変数の変化量を,以下の式で設定する。
この式でを更新していくことによりエビデンスの蓄積過程をシミュレートできる。図2の各軌道はこの計算により得られたものである。
標準的なドリフト拡散モデルでは,開始点とドリフト率,および非決定時間は,試行間で変動すると仮定される[1]。ドリフト率の試行間変動は,刺激に対する注意の変動などに対応すると考えられ,標準偏差の正規分布に従って変動すると仮定される。この変動を仮定することで,正反応より誤反応の方が反応時間が長くなるということが説明可能となる。これは,ドリフト率が小さくなる試行において,誤反応が起こりやすくなり,かつ反応時間が長くなるためである。開始点の試行間変動は区間の一様分布に従うと仮定される。これは,ある特定の刺激がどの程度呈示されやすいかについての期待が試行間で変動することを表現する。この変動により,誤反応が起こる試行で反応時間が短くなることが説明できる。これは,開始点が誤反応側の境界に寄っているときに,早い時間帯で誤反応が起きやすくなるためである。また,非決定時間も区間の一様分布に従うと仮定される。
したがって,標準的なドリフト拡散モデルのパラメータは,開始点の平均 (),開始点の試行間変動 (),ドリフト率の平均 (),ドリフト率の標準偏差 (),境界 (),非決定時間の平均 (),非決定時間の試行間変動 () の7つとなる。
反応時間分布および選択確率の解析解
二つの選択に関する上記のモデルにおいて,各パラメータを固定した場合 (試行間変動は仮定しない場合),それぞれの選択肢を選ぶ確率,およびその反応時間の分布は次のように解析的に導出される [1]。下側の境界 (0) に到達し,反応Bが起こる確率は,
となる。ただしドリフト率が0だった場合はこの確率は となる。さらに,反応Bが起こり,かつ (非決定時間を除いた) その反応時間がとなる条件付きの確率密度は
で与えられる。境界に到達し反応Aが起こり,かつその反応時間がとなる確率密度は,上の式においてをで, をで置き換えることで得られる。図2の上下の曲線はこれらの式により得られた条件付きの確率密度関数である。シミュレーションにより得た反応時間のヒストグラムもサンプルが増えるにつれてこの分布に近づいていくことがわかる。
モデルフィッティング
上記のように解析的に得られる反応時間の分布が実際のデータに近づくようにパラメータを調整することで,明示的にドリフト拡散過程をシミュレートせずともモデルのパラメータを推定することができる。また,複数ある候補のモデルからデータをよりよく説明するモデルを選択することも可能となる。パラメータの推定やモデル選択をする作業を総称してモデルフィッティングと呼ぶ。
実験で収集された反応データに対して,モデルフィッティングをする方法として,最小化,最尤法,重み付き最小二乗法,ベイズ推定等がある[9]。モデルフィッティング用のソフトウェアとしては,以下がある。
- Fast-dm[10]: Voss & Voss (2007)が開発したWindowsで動作するソフトウェア。最尤推定,Kolmogorov-Smirnov,最小化などの方法が可能である。
- DMAT[11]: Vandekerckhove & Tuerlinckx (2008)が開発した,ドリフト拡散モデル用MATLABツールボックス。
- EZ2[12]: Wagenmakers, Van Der Maas, & Grasman(2007)によって提案されたドリフト拡散モデルから試行間変動の推定を除いたシンプルなEZ拡散モデルを用いてモデルフィッティングするRパッケージ。
- HDDM[13]: Wiecki, Sofer, & Frank(2013)が開発した,ドリフト拡散モデルを階層ベイズ推定するPythonパッケージ。
- hBayesDM[14]: Ahn, Haines, & Zhang(2017)が開発した,意思決定課題に対して階層ベイズモデリングを行うRパッケージ。
- rtdists(https://github.com/rtdists/rtdists/): ドリフト拡散モデルをはじめとする反応時間のモデリングに有用な関数が含められたRパッケージ。
それぞれのモデルや推定方法には仮定がおかれていることがあり,モデルフィッティングに用いるデータがその仮定に合っているかどうかは事前に確認する必要がある。各種推定法に関する専門家による推奨については,Boehmらの論文[15]にまとめられている。また,ドリフト拡散モデルでのモデルフィッティングにあたっては,十分なデータ数が必要になる。特に反応時間の分布の情報を用いてパラメータ推定する方法の場合は,試行数が100程度の場合は,ドリフト拡散モデルの試行間変動性にかかわるパラメータの推定が真値からずれることが示されている[16]。そのため,試行間変動性にかかわるパラメータの推定を行う場合は,できるだけ多くの試行数が必要になるが,試行数を増やすと参加者の動機づけが低下する,疲れの影響が出る,などの問題も生じる。また,そもそも試行数を増やすことが難しい実験状況も多い[15]。そこで,パラメータ推定にあたり,参加者集団のパタメータの分布も仮定した階層ベイズ推定を行うことで,各参加者の試行数は少なくとも安定した推定する方法も提案されている[17][18]。
適用事例
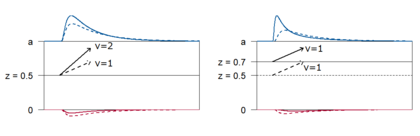
ドリフト拡散モデルを用いることで,反応分布の形状の情報を利用することが可能となり,単純な平均反応時間の解析では取りこぼされていた情報を利用して詳細なプロセスを検討することができる。例えば,開始点パラメータを増加させることと,ドリフト率を増加させることはいずれも反応Aの選択確率を増加させ,その平均的な反応時間を短くする効果があるが,その反応時間分布の形状に与える影響が異なる。図3の左のパネルでは,開始点パラメータを固定し,ドリフト率を増加させている (実線が増加後)。この場合,反応Aの確率が高くなり,速い反応時間の密度が増加するため平均反応時間は短くなるが,反応時間の分布のピーク (最も密度が高くなる位置) はほとんど変化しない。一方,開始点パラメータをに近づけた場合 (図3右) は,反応Aの反応時間分布のピークが速い時間帯にシフトし,分布の歪みが大きくなっている。
ヒトやその他の動物の意思決定には,現在の感覚入力や過去の選択の結果のみならず,過去の選択履歴が次の選択に影響することが知られている。同じ選択を繰り返す傾向は選択の慣性 (inertia) や固執性 (perseverance) と呼ばれている[19]。そのような傾向はドリフト拡散モデルではエビデンスの蓄積の開始点にバイアスを与えるという解釈が可能である。しかし,実際の知覚的意思決定課題における選択データにおいては,過去と同じ選択肢が選ばれる効果は,図3左のように比較的反応が遅い場合でも見られ,そのようなデータは開始点よりはむしろドリフト率が過去と同じ選択をする方向にバイアスがかかるとするモデルでよく説明されることが報告されている[20]。この結果は,選択履歴の効果が,知覚的なエビデンスの蓄積過程に影響するということを示唆している。
ドリフト拡散モデルのパラメータの推定値を利用して,選択に関するプロセスの個人差に影響する要因も検討されている。代表的な事例は加齢の効果について調べたものである。例えば高齢者は一般に多くの認知課題において反応が遅くなることが示されているが,ドリフト拡散モデルを適用して検討した研究では,高齢者の反応には長い非決定時間,そして境界の間隔が大きいという特徴はあるものの,ドリフト率には若年者との違いはないということが報告されている[21]。一方で,幼児では境界分離が大きく,非決定時間が長いことに加え,ドリフト率も比較的小さいことが示されている[22]。また,注意欠如・多動症 (ADHD) や読字障害 (dyslexia) を有する若年者はそうでない統制群に比べ,ドリフト率が低い傾向があることを示した研究もある[23][24]。一般知能 (IQ) との関係に関しては,高IQ群は低IQ群よりドリフト率が2倍程度高いという結果が報告されている [25] [26] 。
神経活動との対応
主にサルを対象とした単一細胞レベルでの神経活動記録により,エビデンスの蓄積過程に対応する神経活動が検討されてきた。例えば視線でターゲットを選択することで反応する意思決定課題においては,ターゲットの方向へのサッケード時に選択的に活動するLIP野 (lateral intraparietal cortex) の細胞は刺激の呈示とともに徐々に活動が増加し,ある閾値に到達したときにサッケード反応が起こるということが観測されており,その振る舞いはエビデンスの蓄積を表現する逐次サンプリングモデルと対応付けられるという議論がある[27]。
その他の逐次サンプリングモデル
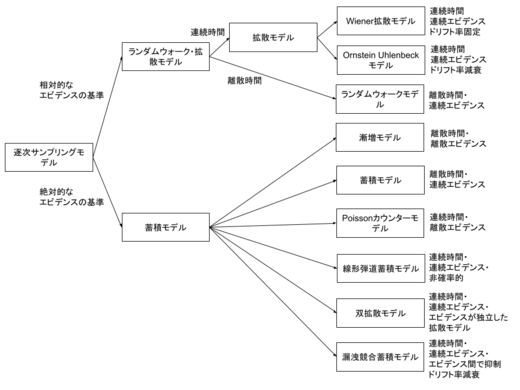
逐次サンプリングモデルは,ドリフト拡散モデルだけではない。図4に示すように,逐次サンプリングモデルは,エビデンスの蓄積に関する基準が絶対的か相対的か,対象とする時間が連続的か離散的か,蓄積するエビデンスが連続的か離散的か,ドリフト率が固定か変化するかなどによって分類することができる。ドリフト拡散モデルは,逐次サンプリングモデルの代表的なモデルであるが,モデルの設定においては複数あるモデルの1つの形式であると言える(代表的な逐次サンプリングモデルのモデル間の差異については,Ratcliff & Smith(2004)[28]を参照)。
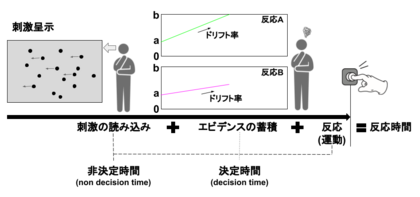
ドリフト拡散モデル以外の代表的な逐次サンプリングモデルとして,線形弾道蓄積モデル[29]がある。図5にあるように,線形弾道蓄積モデルは,ドリフト拡散モデルと類似しているが,エビデンスの蓄積の基準が絶対的なことと確率的ではない点が異なる。ドリフト拡散モデルでは,反応はエビデンス蓄積が上の境界と下の境界のどちらに到達するかで決まる相対的なものであった。一方,線形弾道蓄積モデルでは,それぞれの反応は独立してエビデンスの蓄積を行って,最終的に先に閾値()に到達した反応が出力される(図5の場合,先にに到達した反応Aが出力される)。エビデンスの蓄積が始まる点を開始点()と呼び,選択肢で同一のこともあるが,異なることもある。開始点の位置の違いは,エビデンスの蓄積の前に存在する選択肢に対するバイアスとして解釈される。ドリフト拡散モデルと同様にエビデンスの蓄積の速さはドリフト率()が決めるが,蓄積過程は線形かつ非確率的である。各試行のドリフト率()は,平均,標準偏差の正規分布に従い,各試行の開始点()は,0から(開始点の上限)の一様分布に従う。決定時間は,で求めることができ,非決定時間 ()は,全試行で一定とする。とは,推定するパラメータではなく,が推定するパラメータになる。線形弾道蓄積モデルは,ドリフト拡散モデルよりも推定するパラメータが少なく,2選択肢以外の状況にも適用できるので,ドリフト拡散モデルと合わせて今後の活用が期待できる。
モデルの拡張 (強化学習モデルとの統合)
ドリフト拡散モデルは試行内の刺激呈示から反応出力 (選択) までのプロセスを表現するモデルであるが,試行間の選択傾向の変化を表す他の数理モデルと組み合わせることもできる。例えば,報酬に基づく学習のプロセスを表現する代表的なモデルである強化学習モデルと組み合わせた枠組みが提案されている[30][31]。一般の強化学習モデルでは,行動の結果与えられる報酬に基づいて各行動の価値が計算され,価値の高い行動が高い確率で選択される。ドリフト拡散モデルのドリフト率をこの行動価値の関数にすることで,選択肢の価値の差が小さいほど反応が競合し,反応時間が長くなるという効果を表すことができる。そのように強化学習モデルを用いることで,ドリフト拡散モデルによる反応時間や選択の予測が改善できる。また,逆にドリフト拡散モデルにより反応時間の情報を用いることで,強化学習のパラメータの信頼性も改善される [32]。このように選択傾向の変化と反応時間を同時にモデル化して行動の背後にあるプロセスを探るというアプローチは,実験的に観測される情報をフルに活用できる枠組みとしてさらなる発展が期待される。
参考文献
- ↑ 1.0 1.1 1.2 1.3 Ratcliff, R.(1978).
A theory of memory retrieval.
Psychological Review 1978, 85(2);59–108 - ↑ 2.0 2.1
Ratcliff, R., Smith, P.L., Brown, S.D., & McKoon, G. (2016).
Diffusion Decision Model: Current Issues and History. Trends in cognitive sciences, 20(4), 260-281. [PubMed:26952739] [PMC] [WorldCat] [DOI] - ↑
Ratcliff, R., Thapar, A., & McKoon, G. (2003).
A diffusion model analysis of the effects of aging on brightness discrimination. Perception & psychophysics, 65(4), 523-35. [PubMed:12812276] [PMC] [WorldCat] [DOI] - ↑
Smith, P.L., Ratcliff, R., & Wolfgang, B.J. (2004).
Attention orienting and the time course of perceptual decisions: response time distributions with masked and unmasked displays. Vision research, 44(12), 1297-320. [PubMed:15066392] [WorldCat] [DOI] - ↑
Ratcliff, R., Gomez, P., & McKoon, G. (2004).
A diffusion model account of the lexical decision task. Psychological review, 111(1), 159-82. [PubMed:14756592] [PMC] [WorldCat] [DOI] - ↑
Ratcliff, R. (2014).
Measuring psychometric functions with the diffusion model. Journal of experimental psychology. Human perception and performance, 40(2), 870-88. [PubMed:24446719] [PMC] [WorldCat] [DOI] - ↑
White, C.N., Ratcliff, R., Vasey, M.W., & McKoon, G. (2010).
Using diffusion models to understand clinical disorders. Journal of mathematical psychology, 54(1), 39-52. [PubMed:20431690] [PMC] [WorldCat] [DOI] - ↑
Krajbich, I., Armel, C., & Rangel, A. (2010).
Visual fixations and the computation and comparison of value in simple choice. Nature neuroscience, 13(10), 1292-8. [PubMed:20835253] [WorldCat] [DOI] - ↑
Ratcliff, R., & Tuerlinckx, F. (2002).
Estimating parameters of the diffusion model: approaches to dealing with contaminant reaction times and parameter variability. Psychonomic bulletin & review, 9(3), 438-81. [PubMed:12412886] [PMC] [WorldCat] [DOI] - ↑
Voss, A., & Voss, J. (2007).
Fast-dm: a free program for efficient diffusion model analysis. Behavior research methods, 39(4), 767-75. [PubMed:18183889] [WorldCat] [DOI] - ↑
Vandekerckhove, J., & Tuerlinckx, F. (2008).
Diffusion model analysis with MATLAB: a DMAT primer. Behavior research methods, 40(1), 61-72. [PubMed:18411528] [WorldCat] [DOI] - ↑
Wagenmakers, E.J., van der Maas, H.L., & Grasman, R.P. (2007).
An EZ-diffusion model for response time and accuracy. Psychonomic bulletin & review, 14(1), 3-22. [PubMed:17546727] [WorldCat] [DOI] - ↑
Wiecki, T.V., Sofer, I., & Frank, M.J. (2013).
HDDM: Hierarchical Bayesian estimation of the Drift-Diffusion Model in Python. Frontiers in neuroinformatics, 7, 14. [PubMed:23935581] [PMC] [WorldCat] [DOI] - ↑
Ahn, W.Y., Haines, N., & Zhang, L. (2017).
Revealing Neurocomputational Mechanisms of Reinforcement Learning and Decision-Making With the hBayesDM Package. Computational psychiatry (Cambridge, Mass.), 1, 24-57. [PubMed:29601060] [PMC] [WorldCat] [DOI] - ↑ 15.0 15.1 Boehm, U., Annis, J., Frank, M. J., Hawkins, G. E., Heathcote, A., Kellen, D., Krypotos, A.-M., Lerche, V., Logan, G. D., Palmeri, T. J., van Ravenzwaaij, D., Servant, M., Singmann, H., Starns, J. J., Voss, A., Wiecki, T. V., Matzke, D., & Wagenmakers, E.-J.(2018).
Estimating across-trial variability parameters of the Diffusion Decision Model: Expert advice and recommendations.
Journal of Mathematical Psychology, 87, 46–75 - ↑
Vandekerckhove, J., & Tuerlinckx, F. (2007).
Fitting the Ratcliff diffusion model to experimental data. Psychonomic bulletin & review, 14(6), 1011-26. [PubMed:18229471] [WorldCat] [DOI] - ↑
Wiecki, T.V., Sofer, I., & Frank, M.J. (2013).
HDDM: Hierarchical Bayesian estimation of the Drift-Diffusion Model in Python. Frontiers in neuroinformatics, 7, 14. [PubMed:23935581] [PMC] [WorldCat] [DOI] - ↑
Ahn, W.Y., Haines, N., & Zhang, L. (2017).
Revealing Neurocomputational Mechanisms of Reinforcement Learning and Decision-Making With the hBayesDM Package. Computational psychiatry (Cambridge, Mass.), 1, 24-57. [PubMed:29601060] [PMC] [WorldCat] [DOI] - ↑
Akaishi, R., Umeda, K., Nagase, A., & Sakai, K. (2014).
Autonomous mechanism of internal choice estimate underlies decision inertia. Neuron, 81(1), 195-206. [PubMed:24333055] [WorldCat] [DOI] - ↑
Urai, A.E., de Gee, J.W., Tsetsos, K., & Donner, T.H. (2019).
Choice history biases subsequent evidence accumulation. eLife, 8. [PubMed:31264959] [PMC] [WorldCat] [DOI] - ↑
Ratcliff, R., Thapar, A., & McKoon, G. (2010).
Individual differences, aging, and IQ in two-choice tasks. Cognitive psychology, 60(3), 127-57. [PubMed:19962693] [PMC] [WorldCat] [DOI] - ↑
Ratcliff, R., Love, J., Thompson, C.A., & Opfer, J.E. (2011).
Children are not like older adults: a diffusion model analysis of developmental changes in speeded responses. Child development, 83(1), 367-81. [PubMed:22188547] [PMC] [WorldCat] [DOI] - ↑
Mulder, M.J., Bos, D., Weusten, J.M., van Belle, J., van Dijk, S.C., Simen, P., ..., & Durston, S. (2010).
Basic impairments in regulating the speed-accuracy tradeoff predict symptoms of attention-deficit/hyperactivity disorder. Biological psychiatry, 68(12), 1114-9. [PubMed:20926067] [WorldCat] [DOI] - ↑
Zeguers, M.H., Snellings, P., Tijms, J., Weeda, W.D., Tamboer, P., Bexkens, A., & Huizenga, H.M. (2011).
Specifying theories of developmental dyslexia: a diffusion model analysis of word recognition. Developmental science, 14(6), 1340-54. [PubMed:22010894] [WorldCat] [DOI] - ↑
Ratcliff, R., Thapar, A., & McKoon, G. (2010).
Individual differences, aging, and IQ in two-choice tasks. Cognitive psychology, 60(3), 127-57. [PubMed:19962693] [PMC] [WorldCat] [DOI] - ↑
Ratcliff, R., Thapar, A., & McKoon, G. (2011).
Effects of aging and IQ on item and associative memory. Journal of experimental psychology. General, 140(3), 464-87. [PubMed:21707207] [PMC] [WorldCat] [DOI] - ↑
Shadlen, M.N., & Newsome, W.T. (1996).
Motion perception: seeing and deciding. Proceedings of the National Academy of Sciences of the United States of America, 93(2), 628-33. [PubMed:8570606] [PMC] [WorldCat] [DOI] - ↑
Ratcliff, R., & Smith, P.L. (2004).
A comparison of sequential sampling models for two-choice reaction time. Psychological review, 111(2), 333-67. [PubMed:15065913] [PMC] [WorldCat] [DOI] - ↑
Brown, S.D., & Heathcote, A. (2008).
The simplest complete model of choice response time: linear ballistic accumulation. Cognitive psychology, 57(3), 153-78. [PubMed:18243170] [WorldCat] [DOI] - ↑
Pedersen, M.L., Frank, M.J., & Biele, G. (2017).
The drift diffusion model as the choice rule in reinforcement learning. Psychonomic bulletin & review, 24(4), 1234-1251. [PubMed:27966103] [PMC] [WorldCat] [DOI] - ↑
Frank, M.J., Gagne, C., Nyhus, E., Masters, S., Wiecki, T.V., Cavanagh, J.F., & Badre, D. (2015).
fMRI and EEG predictors of dynamic decision parameters during human reinforcement learning. The Journal of neuroscience : the official journal of the Society for Neuroscience, 35(2), 485-94. [PubMed:25589744] [PMC] [WorldCat] [DOI] - ↑
Shahar, N., Hauser, T.U., Moutoussis, M., Moran, R., Keramati, M., NSPN consortium, & Dolan, R.J. (2019).
Improving the reliability of model-based decision-making estimates in the two-stage decision task with reaction-times and drift-diffusion modeling. PLoS computational biology, 15(2), e1006803. [PubMed:30759077] [PMC] [WorldCat] [DOI]
















![{\displaystyle [z-s_{z},z+s_{z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0201c94118034f723338d72b1141065f2dc8bcf3)
![{\displaystyle [T_{er}-s_{t},T_{er}+s_{t}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e8082a57f32d18f5043bc490dff8a03730bda4a)



















