「視覚系の順逆変換モデル」の版間の差分
細編集の要約なし |
細編集の要約なし |
||
| 2行目: | 2行目: | ||
<font size="+1">[http://researchmap.jp/inui_toshio 乾 敏郎]</font><br> | <font size="+1">[http://researchmap.jp/inui_toshio 乾 敏郎]</font><br> | ||
''追手門学院大学''<br> | ''追手門学院大学''<br> | ||
DOI:<selfdoi /> | DOI:<selfdoi /> 原稿受付日:2021年6月28日 原稿完成日:2021年7月XX日<br> | ||
担当編集委員:[https://researchmap.jp/123qweasd 五味 裕章](NTTコミュニケーション科学基礎研究所)<br> | 担当編集委員:[https://researchmap.jp/123qweasd 五味 裕章](NTTコミュニケーション科学基礎研究所)<br> | ||
</div> | </div> | ||
2021年7月21日 (水) 12:50時点における版
乾 敏郎
追手門学院大学
DOI:10.14931/bsd.9871 原稿受付日:2021年6月28日 原稿完成日:2021年7月XX日
担当編集委員:五味 裕章(NTTコミュニケーション科学基礎研究所)
英:forward-inverse optics model
視覚系は対象の様々な視覚属性を二次元網膜像から非常に短時間で推定し、知覚している。川人と乾 (1990)は、視覚の不良設定問題を短時間で解くモデルとして順逆変換モデルを提案した。順変換(順光学)は3次元世界から2次元網膜像を生成する変換であり、逆変換(逆光学)は2次元網膜像から3次元世界の属性を推定する変換である。モデルでは、視覚系では上行性結合(前向き結合)によって近似逆変換が計算され、下行性結合(後ろ向き結合)によって順変換が計算される。この順変換と近似逆変換の計算ループを通じて、速くかつ正確に外界の属性が推定されることが示された。
対象のさまざまな視覚属性は2次元網膜像から推定されている。属性の多くは、3次元であり、2次元網膜像から3次元属性の推定は一般には解けない不良設定問題(ill-posed problem)である。3次元世界から2次元網膜像を作る画像生成過程は、物理法則に従っていて、順光学(forward optics)と呼ばれる。対象の属性は、この逆の過程を経て推論されなければならない。
脳の計算は、基本的に階層的ベイズ推定の枠組みでとらえられている(たとえば、文献[1])。ベイズ推定は、ベイズの公式
- (事後確率)(事前確率)(条件付確率)
から事後確率を最大にする原因を特定することによって推論する(これを最大事後確率推定と呼ぶ)。事前確率は先験的知識である。そして、脳は高速に最大事後確率推定によって網膜像から外界の状態や構造を推定していると考えられた。一方、我々が正しく外界を知覚できるのは、一般の自然界で成立する何らかの制約条件を用いて、この逆問題(不良設定問題)を解いているからだと考えられている(逆光学;inverse optics)。
川人と乾 (1990)[2]は以下のような理論を提案した。まずHorn (1975) [3]の画像放射照度方程式(image irradiance equation)を一般化した次の画像生成方程式を基本に考える。
左辺は、二次元画像強度データを示し、左眼の画像か右眼の画像の網膜上の位置での、時間、波長の光強度を示す。とすると、右辺は視覚世界の状態や構造から画像データが決まる画像生成過程を非線形関数で表したものである。の中の変数はすべて視覚大脳皮質で別々に表現され再構成されていると考える。具体的なとして、画像強度のある方向への1階微分と2階微分、局所的な速度や、両眼視または単眼視によって得られた奥行きや面の傾き、面の色、照明光の色や光源位置、物体の3次元的空間位置、観察者自身の移動速度ベクトルなどである。
視覚の目的はからを推定することである。マルコフ確率場(Markov random field)理論を用いると最大事後確率推定は、以下の事後エネルギーの最小化として定式化される。具体的には、の事前確率(内部モデル)を 、が与えられたときのの条件つき確率をで表す。そして、これらがGibbs分布に従うと仮定して、対応するエネルギーを、とすると、事後エネルギーは、
と書くことができる。この事後エネルギーを最小化することによって最大事後確率推定ができる(たとえば、文献[4][1]参照)。
これを解くために、視覚大脳皮質はその並列階層構造に上式右辺の画像生成過程の近似逆変換と順変換を埋め込んでいると仮定する。具体的には、
とする。そして大脳皮質一次視覚野から高次視覚野への上行性(前向き)神経結合によっての近似逆変換(すなわち近似逆光学)が計算され、高次視覚野から一次視覚野への下行性(後向き)神経結合によって順光学が計算されると仮定する。そして事後エネルギー最小化が次式で表すような神経回路モデルで計算されていると仮定する(図)。
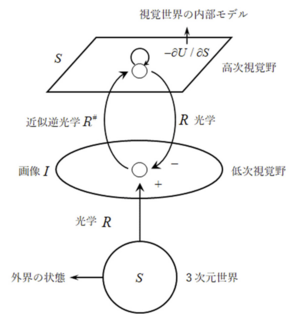
図では、2次元画像データは視覚下位中枢に、視覚世界の様子は視覚上位中枢に表現されている。このモデルは視覚下位中枢を折返しにして鏡像対称となっている。このとき、領野間の前向きと後ろ向きの結合ループを信号が循環する間に正しい解に到達することが示された。
図に示したモデルは、をひとまとめにして記述したモデルである。実際には、からが、一次視覚野から高次視覚野で別々に表現されており、各階層間で上記の順逆変換のループが働いて各属性が推定されると考えられている。これらの計算過程やそれを支持する生理学や解剖学の知見については、文献[2][5]を参照。
なお、知覚の計算を行うときには前向きと後ろ向きの神経回路が用いられるが、後ろ向きの結合は、順光学なので仮に外部刺激による信号がないときに働けば、知覚時と同じ活動を再現することが可能である。つまりこのような順逆変換が学習されれば(彼らの理論では学習アルゴリズムも与えている)外界の情報の処理と内的イメージの生成が同時に可能になるのである。具体的な視覚問題に適用された例は、文献[6]にある。なおこの理論は、Fristonの脳の統一理論である自由エネルギー原理において拡張された[7][8]。
参考文献
- ↑ 1.0 1.1 乾 敏郎 (2004).
視覚計算とマルコフ確率場。 石黒 真木夫・松本 隆・乾 敏郎・田邉 國士(著)「統計科学のフロンティア」第4巻『階層ベイズモデルとその周辺-時系列・画像・認知への応用-』 岩波書店, 171-233. - ↑ 2.0 2.1 川人 光男・乾 敏郎 (1990).
視覚大脳皮質の計算理論。電子情報通信学会論文誌D-II, 73:1111-1121。 - ↑ Horn, B. K. P. (1975).
Obtaining shape from shading information. In: Winston, P. H. (Ed.) The Psychology of Computer Vision. New York, McGraw-Hill. 115-155. - ↑ 川人 光男 (1996).
『脳の計算理論』 産業図書。 - ↑ 乾 敏郎 (1993).
『Q&Aでわかる脳と視覚-人間からロボットまで』 サイエンス社. - ↑ Kawato, M., Hayakawa, H., & Inui, T. (1993).
A forward-inverse optics model of reciprocal connections between visual cortical areas. Network: Computation in Neural Systems, 4, 415-422. doi: 10.1088/0954-898X_4_4_001 - ↑
Friston, K., Kilner, J., & Harrison, L. (2006).
A free energy principle for the brain. Journal of physiology, Paris, 100(1-3), 70-87. [PubMed:17097864] [WorldCat] [DOI] - ↑ 乾 敏郎・阪口 豊 (2020).
『脳の大統一理論 -自由エネルギー原理とは何か-』 岩波書店。





















![{\displaystyle U(S|I)=1/2[R^{\#}\{I-R(S)\}]^{2}+U(S)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6e73f4d691a9b0abb499ff8df24e5eee2970c85)



