「受容野」の版間の差分
細編集の要約なし |
Hirokitanaka (トーク | 投稿記録) 細編集の要約なし |
||
| (4人の利用者による、間の127版が非表示) | |||
| 1行目: | 1行目: | ||
== 受容野の概念と概要 == | |||
=== 受容野 === | |||
個体は、周囲の環境あるいは体内の変化を刺激としてとらえ知覚することができる。これは感覚受容器で物理エネルギーから電気信号へと変換された刺激情報が大脳皮質感覚野を含む感覚処理経路に沿って伝達されることによる。このとき経路の個々の細胞は自身の電気活動を増加あるいは減少させることで刺激情報の処理伝達を行うが、末梢の特定の部位に生じた刺激しか取り扱わない。この限られた末梢部位の範囲を細胞の受容野とよぶ。視覚の場合は、細胞が光刺激を受け取る網膜の範囲(あるいはその部位に対応する視野範囲)を意味し、体性感覚では、細胞が触、圧、痛、温冷などの刺激を受け取る体部位の範囲を指す。 | |||
受容野の最初の明確な定義はH. K. Hartline (1940) による<ref>'''H. K. Hartline '''<br>The receptive fields of optic nerve fibers. <br>Am. J. Physiol: 1940. 130. 690-699.</ref>。彼は、スポット光にたいするカエル網膜神経節細胞の活動を調べたところ、網膜のある範囲に光を照射したとき、あるいは光を取り除いたときにのみ細胞が興奮応答することを見いだし、この範囲を受容野と定義した。 | |||
=== | === 受容野構造 === | ||
後述するように、ネコの網膜神経説細胞は、受容野の中心付近に照射する場合とその周囲に照射する場合とで反応が異なり、一方では興奮応答し他方では抑制応答する<ref name=ref2><pubmed> 13035466 </pubmed></ref>。このように細胞が刺激を受けとる様式は受容野内部で一様でなく、その内部的な構造は受容野構造(receptive field structure)と呼ばれている。 | |||
同じ感覚系でも受容野構造はその処理段階で大きく異なる。これは、感覚処理経路において前段階の出力が収斂と分散を繰り返しながら次段階へと送られていくためである。一般に初期段階では狭く単純な構造の受容野がみられるのにたいし、高次の段階になると広く複雑な構造の受容野がみられる。とくに、初期段階の細胞の受容野は、その内部に複数の刺激が呈示されても、入力信号は単純に線形加算(linear summation)されるだけの場合が多い。このような受容野は線形受容野(linear receptive field)と呼ばれ、その構造は単純な空間フィルターとして表すことができる。一方、高次の段階では、受容野内部での信号の加算の仕方は非線形(nonlinear)なものとなり、受容野構造は、複数の空間フィルターや整流機構(rectification)などを縦列、並列に組み合わせた複雑な回路様の機構として記述される。 | |||
受容野構造は感覚経路の各段階の細胞がどのような刺激情報を伝達しうるのかを知るための強い手がかりを与える。たとえば、上記の網膜神経節細胞の受容野構造は一様な光よりも明暗のコントラストを照射したときに強い興奮を細胞に引き起こすので、このような細胞は明暗コントラストの伝達に適していると解釈できる。したがって受容野構造を明らかにすることは感覚系を理解する上で極めて重要である。 | |||
== 視覚系の受容野 == | |||
=== 古典的受容野と逆相関法 === | |||
受容野内部に呈示された視覚刺激は、細胞を興奮させることも抑制することもある。単独で呈示された刺激が細胞応答を変化させる空間範囲を古典的受容野(classical receptive field, CRF)と呼ぶ。視覚系で受容野と呼ぶ場合は古典的受容野を指す場合が多い。古典的受容野の周囲には非古典的受容野(non classical receptive field, nCRF)と呼ばれる領域があるが、これについては後述する。 | |||
古典的受容野を計測するために古くから行われてきた手法は、受容野の大きさと比較して十分小さなスポット光やスリット光などを一定間隔で区分けした視野の様々な位置に一定期間呈示し、その期間に生じた細胞のスパイク数を計測して、細胞がどの部位から入力を受け取るのかを決める方法である。しかし、この手法では、インターバルを挟みながら1回ごとに異なる位置に刺激を呈示するため、計測位置の数が多くなるにつれて、膨大な計測時間が必要となる。 | |||
この問題を解決し、比較的短時間で受容野構造を詳細に計測する方法が逆相関法(reverse correlation)である <ref name=ref3><pubmed> 5667803 </pubmed></ref> 。いくつかのバリエーションがあるがここではスパースノイズと呼ばれる刺激を用いる方法を説明する<ref name=ref4><pubmed> 3437330 </pubmed></ref> <ref name=ref5><pubmed> 8492152 </pubmed></ref>。この方法では、先の方法のように刺激位置ごとに試行を分けるのではなく、10ミリ秒程度のフラッシュ光をさまざまな位置にランダムに連続呈示し、この期間のスパイク活動を連続計測する。受容野構造を求める際には、刺激位置ごとにカウンターを設けておき、測定した各スパイクについて、それが生じた一定時間前(この時間のことを遅延時間とよぶ)に呈示されていた刺激位置のカウンターを1増やすという操作を行う。これを全スパイクについてこの操作を行うことで得られるカウンターの空間マップは、細胞がどの空間位置の刺激にたいして発火しやすいのかを表す受容野構造そのものとなっている。 | |||
=== | === 時空間受容野 === | ||
細胞は、空間的に外界の信号を加算して信号を瞬時に出力するわけでなく、過去一定時間内の入力信号を加算して出力する。細胞の現在の出力が、過去に呈示された信号にどのように依存するのかを表した時間特性を時間受容野 (temporal receptive field)とよぶ。時間受容野は、別の見方をすれば、外界刺激の呈示後、どのようなタイミングで細胞が発火しやすいのかという応答の時間特性を表していると捉えることもできる。時間特性を考慮しないときの受容野を空間受容野(spatial receptive field)という。空間受容野と時間受容野を合わせて時空間受容野(spatiotemporal receptive field)と呼んでいる。 | |||
逆相関法において遅延時間を変えれば、細胞がスパイクを発する前の各時点での空間受容野が得られる 。これは時空間受容野そのものである。このように効率よく時空間受容野を求めることができることは逆相関法の大きな利点である。 | |||
=== | === 網膜、視床中継核でみられる受容野構造 === | ||
眼球に入った視覚情報は、視細胞(photoreceptor)で受容されたのち視神経を介して視床外側膝状体(Lateral Geniculate Nucleus, LGN)で中継され、大脳皮質第一次視覚野(Primary visual cortex, V1野)へと至る。この経路を皮質下視覚伝導路と呼ぶ。以下にこの経路における受容野構造をみていく。 | |||
外界の光を電気信号に変換する視細胞には桿体(rod)、錐体(cone)と2種類があり、前者は暗所視に、後者は明所視、色覚に関与している。いずれの受容野も概ね円状で、サイズは非常に小さく、中心窩(fovea)では視野角にして0.5分程度(1/120度)である。 [6] | |||
視細胞からの入力を受け取る双極細胞(bipolar cell)や次の段階に位置する網膜神経節細胞(retinal ganglion cell)は、それぞれ次の2つのタイプのものがある <ref name=ref2 />[7]。第1のものは、受容野の中心領域(center)に明るい光を照射したときに興奮応答し、暗い光を照射したとき(あるいは明るい光をオフしたとき)に抑制応答するもので、ON中心型(ON-center type)と呼ばれる。第2のものは、暗い光に興奮し明るい光に抑制を受けるものでOFF中心型(OFF-center type)とよばれる。いずれのタイプも、中心領域の周囲に光を照射したときには、中心領域と逆の応答をする。すなわち、ON中心型細胞は周辺部(surround)に明るい光を受けたときに抑制を受け、暗い光を受けたときには興奮応答する。またOFF中心型細胞は、周辺部では明るい光に興奮、暗い光に抑制応答がみられる。そこで、前者の受容野構造をON中心OFF周辺型(ON-center OFF-surround)とよび(図2A)、逆のタイプをOFF中心ON周辺型(OFF-center ON-surround)とも呼んでいる(図2B)。中心領域と周辺領域は同心円状に配置しており、2つの領域が逆の反応を示すことからこのような受容野構造を中心周辺拮抗型(antagonistic center-surround)とぶ。このような構造をもつ細胞は、図2Cのように2次元のサイン波刺激でテストしたとき、明るい光がON領域に、暗い光がOFF領域に入るときには反応するが(図2C上)、光が一様に入るときには(図2C下)ほとんど反応しないことから、明暗コントラストのエッジ幅や位置の情報を伝達していると捉えることができる。 | |||
== | [[Image:RetinalGanglisonCell.png|600px]]<br> 中心周辺拮抗型の受容野構造は2つのガウス関数の差分であるDOG(Difference of Gaussian)関数で表すことができる(図2A, Bの下段)<ref name=ref8><pubmed> 5862581 </pubmed></ref>。また線形性をもつために、細胞の応答は入力刺激とDOG関数の線形畳み込みで近似できる。ただし、このような近似が十分に成り立つ細胞とそうでない細胞が存在し、前者をX細胞、後者をY細胞という<ref name=ref9><pubmed> 16783910 </pubmed></ref>。 | ||
LGNの受容野構造は網膜神経節細胞とほぼ同一であり、中心周辺拮抗型の同心円構造をもつ。これは個々のLGNニューロンが1つの網膜神経節細胞からの投射のみで、その反応特性が形成されているためと考えられている <ref name=ref10><pubmed> 4093882 </pubmed></ref>。 | |||
=== | === 第一次視覚野(V1野)でみられる受容野構造 === | ||
網膜神経節細胞あるいはLGNの細胞に細長いスリット光を呈示するとき、その向き(方位)を変えても反応は変化しない。このことは、これらの細胞の受容野構造が同心円状であることから予想できる。これにたいし、第一次視覚野の大部分の細胞はスリット光が特定の方位を向くときにのみ選択的に反応する。この方位選択性(orientation selectivity)と呼ばれる特性をもつ細胞の古典的受容野構造は以下の2種類のものがある<ref name=ref11><pubmed> 14403679 </pubmed></ref> <ref name=ref12><pubmed> 4966457 </pubmed></ref>。1つは明るい光に興奮応答するON領域と暗い光に応答するOFF領域が隣あって同じ向きに並んだ構造であり、このような構造をもつ細胞を単純型細胞(simple cell)と呼ぶ(図3A)。もう1種類はON領域とOFF領域が重なりあった細胞でこれを複雑型細胞(complex cell)と呼ぶ(図3B)。 | |||
=== | [[Image:V1RF.png|600px]]<br> 単純型細胞の古典的受容野は、X細胞の受容野と同様、強い線形性を示し、自身のON領域、OFF領域ともっともよくあった刺激を最適とする。たとえば2次元サイン波を刺激とする場合、その明暗がON領域、OFF領域とマッチするような方位、空間周波数(spatial frequency)(=周期の逆数)、位相(phase)をもつものが最適となる(図3A参照)。この仕組みが単純型細胞の方位選択性、空間周波数選択性、位相選択性の基盤になっている。ON、OFF領域が伸びる軸、大きさ、位置関係は細胞に様々であり、したがって単純型細胞は全体として様々な方位、空間周波数、位相に選択性を示す。単純型細胞の古典的受容野は線形性が強く、視覚刺激にたいする応答は、その受容野構造と刺激波形の線形畳み込み(linear convolution)を行った結果に、0以下の信号を出力しない半波整流(half rectification)をとおすことで十分予測できる<ref name= ref13><pubmed> 722589 </pubmed></ref> <ref name= ref14><pubmed> 1450099 </pubmed></ref>。 | ||
複雑型細胞も、単純型細胞と同程度の強い方位選択性や空間周波数選択性を示す。しかし、複雑型細胞は位相に感受性を示さず、受容野内部に入る刺激なら位置によらず同じ方位選択性、空間周波数選択性を示す。このような性質は複雑型細胞が単純型細胞から入力を受け取ることで出来上がると考えられている。この仕組みについては後述する。 | |||
=== | === ガボール関数による単純型細胞の受容野構造近似と画像表現 === | ||
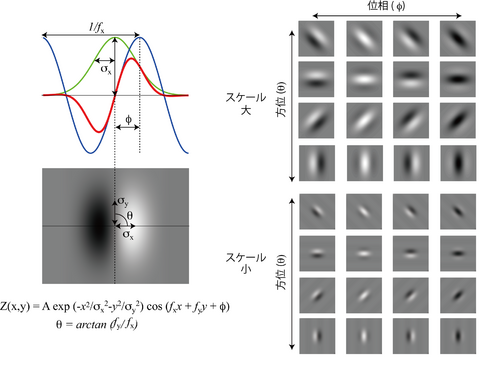
単純型細胞の古典的受容野は、図4に示すガウス関数(緑)とサイン波(青)の積であるガボール関数(Gabor function)(赤、図4の式参照)でよく近似できることが知られている<ref name=ref4 />。ガボール関数のパラメーターを変えることで、サイズ(σx, σy)、方位(θ)、空間周波数(fx, fy)、そして位相(φ)の異なる様々な構造を表すことができる。 | |||
[[Image:GaborFilter.png|500px]] | |||
様々な形のガボール型受容野構造が視野の各位置に一セット揃っており、その結果、画像情報は、網膜視細胞での画素表現から、V1野の単純型細胞のレベルでは、ガボール関数のセットを基底成分とする表現へと変換されて伝達されることになる。この表現には画像情報を効率的に伝達する上でいくつかの望ましい特性がある。第一に、分解された画像成分は高次視覚野へと伝達されて利用されるので、初期の段階では画像情報は失われないようにする必要があるが、ガボール関数を用いた分解表現ではそれが十分実現されていることが示されている<ref>'''J. G. Daugman '''<br>Complete discrete 2-D Gabor transforms by neural networks for image analysis and compression. <br>IEEE Transactions on In Acoustics, Speech and Signal Processing: 1988, 36(7), 1169-1179.</ref>。さらに、ガボール関数により、自然画像はスパースコーディング(sparse coding)という非常に効率のよい方式で伝達できることも知られており、視覚系が自然界の膨大な画像情報を少ないエネルギーで伝送できる鍵になっていると考えられている <ref name= ref15><pubmed> 8637596 </pubmed></ref>。 | |||
=== | === 単純型細胞の時空間受容野構造と運動方向選択性、両眼受容野構造 === | ||
単純型細胞の大半は物体の動きを検出するのに適した受容野構造をもつ。図5はそのような例(模式図)である(元来時空間受容野構造は空間2次元+時間1次元の合計3次元の構造であるが、紙面で表すために、細胞の最適方位に沿って空間受容野を1次元につぶし横軸にとり、時空間の2次元で表している)。現在に向かって(図では下方に向かって)、実線で表すON領域、点線が表すOFF領域ともに左へとずれている。このような受容野構造は、線分状の刺激がその軸と直交する軸上で左へ動くとき多くの入力信号を受けることができ細胞を興奮させるが、右向きに動くときや、止まっているときにはあまり信号を受け取ることはできない。一方、このようなON領域、OFF領域の動きがみられない受容野構造も存在し、そのような細胞は方向選択性をもたない。運動方向選択性のある時空間受容野は、それをもたない受容野を適当に足し合わせることで作り出せることが知られている。 [16] | |||
第一次視覚野細胞では視覚伝導路において左右両眼からの情報がはじめて収斂するため、多くの細胞が両眼に受容野をもつ。単純型細胞の左右眼の受容野構造は、向きや空間周波数は同じであるが、位相あるいは位置が異なる場合が多い。この位相あるいは位置のずれかたは細胞により様々である。単純型細胞は、このずれにより、奥行き知覚の手がかりとなる網膜上の両眼視差(binocular disparity)に感受性をもつことが知られており、この知覚に重要な役割を担っている。[17] | |||
=== | === 複雑型細胞の受容野構造 === | ||
複雑型細胞も単純型細胞と同様に、サイン波刺激にたいして、強い方位、空間周波数、運動方向の選択性をもっている。しかしながら、ON、OFF領域はオーバーラッップしておりその構造からこれらの選択性を予測することはできない。また単純型細胞と異なり位相に選択性は示さない。これらの選択性は、同じ方位や、空間周波数選択性をもち、受容野位相だけが異なる単純型細胞からの入力が収斂することでできあがっていると考えられている。これを最も単純化したモデルが図6に示すエネルギーモデル(energy model)で、このモデルでは90度位相の異なる2つの単純型細胞の出力が2乗されることで複雑型細胞の受容野構造をつくっている。2つの単純型細胞のON,OFF領域が、同じ時間受容野をもつときに、複雑型細胞の同じ特性の時間受容野をもつことになり、その運動方向選択性が説明される。時空間受容野も含めたエネルギーモデルは運動エネルギーモデル(motion energy model)と呼ばれている。 | |||
複雑型細胞の多くはまた、刺激の位置や明暗のコントラスに影響されることのなく両眼視差を検出できることが知られている。この両眼視差検出器としての望ましい性質は、似た両眼視差にチューンした単純型細胞からの出力を集めることでできると考えられている。このような複雑型細胞のモデルは両眼視差エネルギーモデル(disparity energy model)と呼ばれている。 | |||
=== 非古典的受容野 === | === 非古典的受容野 === | ||
古典的受容野の周辺には、刺激が単独で呈示されるときには細胞活動に影響しないが、古典的受容野内部の刺激と同時に呈示されると、細胞に主に抑制性の影響を及ぼす空間範囲があり、これを非古典的受容野と呼んでいる。<br> | |||
非古典的受容野は網膜の段階ですでに存在しており、視覚経路のほとんど全ての段階でみられるが、ここでは最も多くの研究が行われてきたV1野の非古典的受容野について述べる。V1野ではこの構造は周辺領域と呼ばれることも多いが、これは網膜細胞の周辺領域とは全く異なるので注意が必要である。V1野でこの領域は古典的受容野の周囲に一様に広がるのではなく、ある程度の局在化がみられ、最適方位の延長上に広がるもの、最適方位と直交する軸方向に広がるもののほか、斜め方向に位置するものもある。多くは抑制性の影響を及ばすが興奮性の影響も報告されている。また非古典的受容野の抑制には特徴選択性があり、古典的受容野の最適な方位、空間周波数にたいして最も抑制が強くなる。これらの構造は、古典的受容野に最適な縞模様の境界部分を検出するのに適しており、テクスチャー分析に役立っているものと考えられている。とくに、古典的受容野と周辺領域が同じ向きに伸びているものが報告されており、このような構造は異なるテクスチャーのエッジ部分の検出に好都合である。これ以外にも非古典的受容野は、視野に配置された複数刺激の中で1つだけ異なる刺激にたいして細胞が強く応答するポップアップと呼ばれる特性の基盤、あるいは線分の長さや折れ線や曲線の角度や極率を検出するための初期機構としても注目されている。 | |||
=== 高次視覚野における受容野構造 === | |||
霊長類視覚系には30以上もの領域があり、これらの領野はV1野、V2野を経て側頭連合野(temporal lobe)へと至る腹側経路(ventral pathway)と頭頂連合野(parietal lobe)へと至る背側経路(dorsal pathway)の2つの経路として構成されている。多くの領野では受容野構造の詳細はわかっていないが、細胞が伝達する視覚特徴については、適切な刺激セットを用いて細胞の応答に適切な刺激を同定するという方法で数多くの知見が得られている。これに基づき、腹側経路は物体の色、テクスチャーや形の分析に、背側経路は空間情報の伝達に関与していると考えられている。 | |||
細胞の受容野のサイズは高次の領域に向かうにつれて大きくなる。霊長類V1野で中心視野に受容野をもつ細胞の受容野は0.1~1度程度であるが、視覚経路の最終段階に位置するTE野では10度以上にもなる。ただし受容野サイズは偏心度にも依存し、中心視野では小さく、周辺視野ほど大きくなる。例えばV1野の周辺視野の受容野サイズは5度から10度程度である。またV1細胞の受容野位置は対側視野に限られるものが大部分であるが、視覚経路に沿って受容野サイズが大きくなるにつれて、同側視野も含むものが序々に増してくる。TE野ではほとんどの細胞が同側視野を受容野に含む。 | |||
受容野特性は、階層をあがるにつれて序次に複雑な刺激特徴を最適とするものが増してくる。たとえばV2野->V4野->TEO野->TE野と向かう腹側経路では、V2野に折れ線に反応する細胞、V4野にテクスチャーやパターンに反応する細胞、TEO野には物体の部分的特徴、TE野に至っては顔などの極めて複雑な特徴をもつ細胞が存在する。さらに、これらの細胞の多くは、受容野内部で刺激の位置、向き、あるいは形の手がかりを変えても特徴選択性を維持する。 | |||
== 体性感覚系の受容野 == | |||
=== 一次求心性神経繊維の受容野 === | |||
触圧感覚をもたらす機械受容器には皮膚表面知覚に位置するマイスナー小体、メルケル終末と深部にあるパチニ小体、ルフィニ終末の4種類が知られている。マイスナー小体、メルケル終末につながる1次救心性繊維の受容野はスポット状で比較的小さく手では直径数ミリ程度である。パチニ小体、ルフィニ終末につながる繊維の受容野はそれよりも大きく、境界が不明瞭である場合が多い。有毛部には毛の動きを捉える毛包ユニットが知られているが、これらの1次繊維の受容野も四肢末端では直径数ミリ程度である温冷覚の1次繊維の受容野サイズも同定度である。痛覚繊維にも同程度の大きさをもつ比較的受容野の狭い特定的侵害受容ニューロンと、より受容野の大きい広作動閾ニューロンとがある。ただし、いずれの受容器の場合も、体幹に近いところでは受容野サイズは数十平方センチメートルと非常に大きくなる。 | |||
=== 体性感覚野の受容野 === | |||
1次体性感覚野は、視床からの入力が入る3a野、3b野と、そこから入力を受ける2野、1野に区分される。皮膚からの入力は3b野から主に1野へ、筋や腱からの入力は3a野から主に2野へと運ばれる。ただし1野、2野ともに3aおよび3bの両方から入力を受け取り、これらの入力は多くの細胞で収斂している。 | |||
各領野の細胞でみられる受容野サイズは1次繊維と比べるとはるかに大きく、手でも直径数センチメートルある。さらに3a野、3b野より1野や2野のほうが大きい。たとえば3b野の指に受容野をもつ細胞は指一本程度のものが多くあるが、1野や2野には数本の指に受容野が広がるものが数多くみられる。受容野は細胞が存在する大脳半球の反対側に限られる。 | |||
1野や2野の細胞は、3a野や3b野よりも複雑な受容野特性を示すことが知られており、たとえば表皮をこする物体の動きや、物体が伸びる向きや物体表面のテクスチャーなどに選択性を示す細胞が報告されている。 | |||
2次体性感覚野は1次体性感覚野から入力を受け取る。この領野の細胞は1次体性感覚野よりも広い受容野をもち、また体の両側の対称な場所に受容野をもつものが多い。たとえばある細胞は両手の5本指全体に受容野をもつ。さらに、これらの細胞は、皮膚だけでなく、いくつかの筋、腱からの入力が収斂しており、手全体や腕全体といった体の各パーツの姿勢の情報を伝達し、運動の感覚ガイダンスに関与していると考えられている。 <references /> | |||
2012年4月15日 (日) 00:05時点における版
受容野の概念と概要
受容野
個体は、周囲の環境あるいは体内の変化を刺激としてとらえ知覚することができる。これは感覚受容器で物理エネルギーから電気信号へと変換された刺激情報が大脳皮質感覚野を含む感覚処理経路に沿って伝達されることによる。このとき経路の個々の細胞は自身の電気活動を増加あるいは減少させることで刺激情報の処理伝達を行うが、末梢の特定の部位に生じた刺激しか取り扱わない。この限られた末梢部位の範囲を細胞の受容野とよぶ。視覚の場合は、細胞が光刺激を受け取る網膜の範囲(あるいはその部位に対応する視野範囲)を意味し、体性感覚では、細胞が触、圧、痛、温冷などの刺激を受け取る体部位の範囲を指す。
受容野の最初の明確な定義はH. K. Hartline (1940) による[1]。彼は、スポット光にたいするカエル網膜神経節細胞の活動を調べたところ、網膜のある範囲に光を照射したとき、あるいは光を取り除いたときにのみ細胞が興奮応答することを見いだし、この範囲を受容野と定義した。
受容野構造
後述するように、ネコの網膜神経説細胞は、受容野の中心付近に照射する場合とその周囲に照射する場合とで反応が異なり、一方では興奮応答し他方では抑制応答する[2]。このように細胞が刺激を受けとる様式は受容野内部で一様でなく、その内部的な構造は受容野構造(receptive field structure)と呼ばれている。
同じ感覚系でも受容野構造はその処理段階で大きく異なる。これは、感覚処理経路において前段階の出力が収斂と分散を繰り返しながら次段階へと送られていくためである。一般に初期段階では狭く単純な構造の受容野がみられるのにたいし、高次の段階になると広く複雑な構造の受容野がみられる。とくに、初期段階の細胞の受容野は、その内部に複数の刺激が呈示されても、入力信号は単純に線形加算(linear summation)されるだけの場合が多い。このような受容野は線形受容野(linear receptive field)と呼ばれ、その構造は単純な空間フィルターとして表すことができる。一方、高次の段階では、受容野内部での信号の加算の仕方は非線形(nonlinear)なものとなり、受容野構造は、複数の空間フィルターや整流機構(rectification)などを縦列、並列に組み合わせた複雑な回路様の機構として記述される。
受容野構造は感覚経路の各段階の細胞がどのような刺激情報を伝達しうるのかを知るための強い手がかりを与える。たとえば、上記の網膜神経節細胞の受容野構造は一様な光よりも明暗のコントラストを照射したときに強い興奮を細胞に引き起こすので、このような細胞は明暗コントラストの伝達に適していると解釈できる。したがって受容野構造を明らかにすることは感覚系を理解する上で極めて重要である。
視覚系の受容野
古典的受容野と逆相関法
受容野内部に呈示された視覚刺激は、細胞を興奮させることも抑制することもある。単独で呈示された刺激が細胞応答を変化させる空間範囲を古典的受容野(classical receptive field, CRF)と呼ぶ。視覚系で受容野と呼ぶ場合は古典的受容野を指す場合が多い。古典的受容野の周囲には非古典的受容野(non classical receptive field, nCRF)と呼ばれる領域があるが、これについては後述する。
古典的受容野を計測するために古くから行われてきた手法は、受容野の大きさと比較して十分小さなスポット光やスリット光などを一定間隔で区分けした視野の様々な位置に一定期間呈示し、その期間に生じた細胞のスパイク数を計測して、細胞がどの部位から入力を受け取るのかを決める方法である。しかし、この手法では、インターバルを挟みながら1回ごとに異なる位置に刺激を呈示するため、計測位置の数が多くなるにつれて、膨大な計測時間が必要となる。
この問題を解決し、比較的短時間で受容野構造を詳細に計測する方法が逆相関法(reverse correlation)である [3] 。いくつかのバリエーションがあるがここではスパースノイズと呼ばれる刺激を用いる方法を説明する[4] [5]。この方法では、先の方法のように刺激位置ごとに試行を分けるのではなく、10ミリ秒程度のフラッシュ光をさまざまな位置にランダムに連続呈示し、この期間のスパイク活動を連続計測する。受容野構造を求める際には、刺激位置ごとにカウンターを設けておき、測定した各スパイクについて、それが生じた一定時間前(この時間のことを遅延時間とよぶ)に呈示されていた刺激位置のカウンターを1増やすという操作を行う。これを全スパイクについてこの操作を行うことで得られるカウンターの空間マップは、細胞がどの空間位置の刺激にたいして発火しやすいのかを表す受容野構造そのものとなっている。
時空間受容野
細胞は、空間的に外界の信号を加算して信号を瞬時に出力するわけでなく、過去一定時間内の入力信号を加算して出力する。細胞の現在の出力が、過去に呈示された信号にどのように依存するのかを表した時間特性を時間受容野 (temporal receptive field)とよぶ。時間受容野は、別の見方をすれば、外界刺激の呈示後、どのようなタイミングで細胞が発火しやすいのかという応答の時間特性を表していると捉えることもできる。時間特性を考慮しないときの受容野を空間受容野(spatial receptive field)という。空間受容野と時間受容野を合わせて時空間受容野(spatiotemporal receptive field)と呼んでいる。
逆相関法において遅延時間を変えれば、細胞がスパイクを発する前の各時点での空間受容野が得られる 。これは時空間受容野そのものである。このように効率よく時空間受容野を求めることができることは逆相関法の大きな利点である。
網膜、視床中継核でみられる受容野構造
眼球に入った視覚情報は、視細胞(photoreceptor)で受容されたのち視神経を介して視床外側膝状体(Lateral Geniculate Nucleus, LGN)で中継され、大脳皮質第一次視覚野(Primary visual cortex, V1野)へと至る。この経路を皮質下視覚伝導路と呼ぶ。以下にこの経路における受容野構造をみていく。
外界の光を電気信号に変換する視細胞には桿体(rod)、錐体(cone)と2種類があり、前者は暗所視に、後者は明所視、色覚に関与している。いずれの受容野も概ね円状で、サイズは非常に小さく、中心窩(fovea)では視野角にして0.5分程度(1/120度)である。 [6]
視細胞からの入力を受け取る双極細胞(bipolar cell)や次の段階に位置する網膜神経節細胞(retinal ganglion cell)は、それぞれ次の2つのタイプのものがある [2][7]。第1のものは、受容野の中心領域(center)に明るい光を照射したときに興奮応答し、暗い光を照射したとき(あるいは明るい光をオフしたとき)に抑制応答するもので、ON中心型(ON-center type)と呼ばれる。第2のものは、暗い光に興奮し明るい光に抑制を受けるものでOFF中心型(OFF-center type)とよばれる。いずれのタイプも、中心領域の周囲に光を照射したときには、中心領域と逆の応答をする。すなわち、ON中心型細胞は周辺部(surround)に明るい光を受けたときに抑制を受け、暗い光を受けたときには興奮応答する。またOFF中心型細胞は、周辺部では明るい光に興奮、暗い光に抑制応答がみられる。そこで、前者の受容野構造をON中心OFF周辺型(ON-center OFF-surround)とよび(図2A)、逆のタイプをOFF中心ON周辺型(OFF-center ON-surround)とも呼んでいる(図2B)。中心領域と周辺領域は同心円状に配置しており、2つの領域が逆の反応を示すことからこのような受容野構造を中心周辺拮抗型(antagonistic center-surround)とぶ。このような構造をもつ細胞は、図2Cのように2次元のサイン波刺激でテストしたとき、明るい光がON領域に、暗い光がOFF領域に入るときには反応するが(図2C上)、光が一様に入るときには(図2C下)ほとんど反応しないことから、明暗コントラストのエッジ幅や位置の情報を伝達していると捉えることができる。
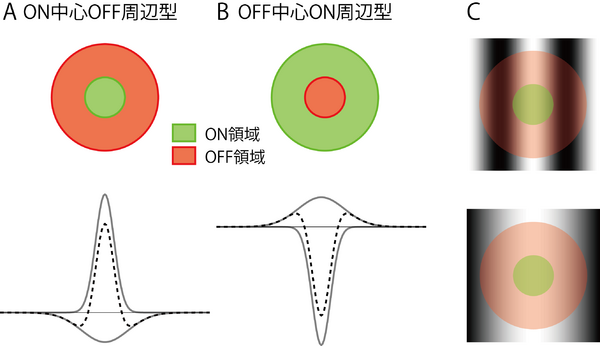
中心周辺拮抗型の受容野構造は2つのガウス関数の差分であるDOG(Difference of Gaussian)関数で表すことができる(図2A, Bの下段)[6]。また線形性をもつために、細胞の応答は入力刺激とDOG関数の線形畳み込みで近似できる。ただし、このような近似が十分に成り立つ細胞とそうでない細胞が存在し、前者をX細胞、後者をY細胞という[7]。
LGNの受容野構造は網膜神経節細胞とほぼ同一であり、中心周辺拮抗型の同心円構造をもつ。これは個々のLGNニューロンが1つの網膜神経節細胞からの投射のみで、その反応特性が形成されているためと考えられている [8]。
第一次視覚野(V1野)でみられる受容野構造
網膜神経節細胞あるいはLGNの細胞に細長いスリット光を呈示するとき、その向き(方位)を変えても反応は変化しない。このことは、これらの細胞の受容野構造が同心円状であることから予想できる。これにたいし、第一次視覚野の大部分の細胞はスリット光が特定の方位を向くときにのみ選択的に反応する。この方位選択性(orientation selectivity)と呼ばれる特性をもつ細胞の古典的受容野構造は以下の2種類のものがある[9] [10]。1つは明るい光に興奮応答するON領域と暗い光に応答するOFF領域が隣あって同じ向きに並んだ構造であり、このような構造をもつ細胞を単純型細胞(simple cell)と呼ぶ(図3A)。もう1種類はON領域とOFF領域が重なりあった細胞でこれを複雑型細胞(complex cell)と呼ぶ(図3B)。
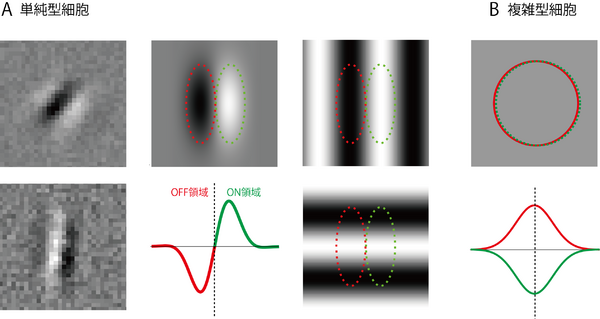
単純型細胞の古典的受容野は、X細胞の受容野と同様、強い線形性を示し、自身のON領域、OFF領域ともっともよくあった刺激を最適とする。たとえば2次元サイン波を刺激とする場合、その明暗がON領域、OFF領域とマッチするような方位、空間周波数(spatial frequency)(=周期の逆数)、位相(phase)をもつものが最適となる(図3A参照)。この仕組みが単純型細胞の方位選択性、空間周波数選択性、位相選択性の基盤になっている。ON、OFF領域が伸びる軸、大きさ、位置関係は細胞に様々であり、したがって単純型細胞は全体として様々な方位、空間周波数、位相に選択性を示す。単純型細胞の古典的受容野は線形性が強く、視覚刺激にたいする応答は、その受容野構造と刺激波形の線形畳み込み(linear convolution)を行った結果に、0以下の信号を出力しない半波整流(half rectification)をとおすことで十分予測できる[11] [12]。
複雑型細胞も、単純型細胞と同程度の強い方位選択性や空間周波数選択性を示す。しかし、複雑型細胞は位相に感受性を示さず、受容野内部に入る刺激なら位置によらず同じ方位選択性、空間周波数選択性を示す。このような性質は複雑型細胞が単純型細胞から入力を受け取ることで出来上がると考えられている。この仕組みについては後述する。
ガボール関数による単純型細胞の受容野構造近似と画像表現
単純型細胞の古典的受容野は、図4に示すガウス関数(緑)とサイン波(青)の積であるガボール関数(Gabor function)(赤、図4の式参照)でよく近似できることが知られている[4]。ガボール関数のパラメーターを変えることで、サイズ(σx, σy)、方位(θ)、空間周波数(fx, fy)、そして位相(φ)の異なる様々な構造を表すことができる。
様々な形のガボール型受容野構造が視野の各位置に一セット揃っており、その結果、画像情報は、網膜視細胞での画素表現から、V1野の単純型細胞のレベルでは、ガボール関数のセットを基底成分とする表現へと変換されて伝達されることになる。この表現には画像情報を効率的に伝達する上でいくつかの望ましい特性がある。第一に、分解された画像成分は高次視覚野へと伝達されて利用されるので、初期の段階では画像情報は失われないようにする必要があるが、ガボール関数を用いた分解表現ではそれが十分実現されていることが示されている[13]。さらに、ガボール関数により、自然画像はスパースコーディング(sparse coding)という非常に効率のよい方式で伝達できることも知られており、視覚系が自然界の膨大な画像情報を少ないエネルギーで伝送できる鍵になっていると考えられている [14]。
単純型細胞の時空間受容野構造と運動方向選択性、両眼受容野構造
単純型細胞の大半は物体の動きを検出するのに適した受容野構造をもつ。図5はそのような例(模式図)である(元来時空間受容野構造は空間2次元+時間1次元の合計3次元の構造であるが、紙面で表すために、細胞の最適方位に沿って空間受容野を1次元につぶし横軸にとり、時空間の2次元で表している)。現在に向かって(図では下方に向かって)、実線で表すON領域、点線が表すOFF領域ともに左へとずれている。このような受容野構造は、線分状の刺激がその軸と直交する軸上で左へ動くとき多くの入力信号を受けることができ細胞を興奮させるが、右向きに動くときや、止まっているときにはあまり信号を受け取ることはできない。一方、このようなON領域、OFF領域の動きがみられない受容野構造も存在し、そのような細胞は方向選択性をもたない。運動方向選択性のある時空間受容野は、それをもたない受容野を適当に足し合わせることで作り出せることが知られている。 [16]
第一次視覚野細胞では視覚伝導路において左右両眼からの情報がはじめて収斂するため、多くの細胞が両眼に受容野をもつ。単純型細胞の左右眼の受容野構造は、向きや空間周波数は同じであるが、位相あるいは位置が異なる場合が多い。この位相あるいは位置のずれかたは細胞により様々である。単純型細胞は、このずれにより、奥行き知覚の手がかりとなる網膜上の両眼視差(binocular disparity)に感受性をもつことが知られており、この知覚に重要な役割を担っている。[17]
複雑型細胞の受容野構造
複雑型細胞も単純型細胞と同様に、サイン波刺激にたいして、強い方位、空間周波数、運動方向の選択性をもっている。しかしながら、ON、OFF領域はオーバーラッップしておりその構造からこれらの選択性を予測することはできない。また単純型細胞と異なり位相に選択性は示さない。これらの選択性は、同じ方位や、空間周波数選択性をもち、受容野位相だけが異なる単純型細胞からの入力が収斂することでできあがっていると考えられている。これを最も単純化したモデルが図6に示すエネルギーモデル(energy model)で、このモデルでは90度位相の異なる2つの単純型細胞の出力が2乗されることで複雑型細胞の受容野構造をつくっている。2つの単純型細胞のON,OFF領域が、同じ時間受容野をもつときに、複雑型細胞の同じ特性の時間受容野をもつことになり、その運動方向選択性が説明される。時空間受容野も含めたエネルギーモデルは運動エネルギーモデル(motion energy model)と呼ばれている。
複雑型細胞の多くはまた、刺激の位置や明暗のコントラスに影響されることのなく両眼視差を検出できることが知られている。この両眼視差検出器としての望ましい性質は、似た両眼視差にチューンした単純型細胞からの出力を集めることでできると考えられている。このような複雑型細胞のモデルは両眼視差エネルギーモデル(disparity energy model)と呼ばれている。
非古典的受容野
古典的受容野の周辺には、刺激が単独で呈示されるときには細胞活動に影響しないが、古典的受容野内部の刺激と同時に呈示されると、細胞に主に抑制性の影響を及ぼす空間範囲があり、これを非古典的受容野と呼んでいる。
非古典的受容野は網膜の段階ですでに存在しており、視覚経路のほとんど全ての段階でみられるが、ここでは最も多くの研究が行われてきたV1野の非古典的受容野について述べる。V1野ではこの構造は周辺領域と呼ばれることも多いが、これは網膜細胞の周辺領域とは全く異なるので注意が必要である。V1野でこの領域は古典的受容野の周囲に一様に広がるのではなく、ある程度の局在化がみられ、最適方位の延長上に広がるもの、最適方位と直交する軸方向に広がるもののほか、斜め方向に位置するものもある。多くは抑制性の影響を及ばすが興奮性の影響も報告されている。また非古典的受容野の抑制には特徴選択性があり、古典的受容野の最適な方位、空間周波数にたいして最も抑制が強くなる。これらの構造は、古典的受容野に最適な縞模様の境界部分を検出するのに適しており、テクスチャー分析に役立っているものと考えられている。とくに、古典的受容野と周辺領域が同じ向きに伸びているものが報告されており、このような構造は異なるテクスチャーのエッジ部分の検出に好都合である。これ以外にも非古典的受容野は、視野に配置された複数刺激の中で1つだけ異なる刺激にたいして細胞が強く応答するポップアップと呼ばれる特性の基盤、あるいは線分の長さや折れ線や曲線の角度や極率を検出するための初期機構としても注目されている。
高次視覚野における受容野構造
霊長類視覚系には30以上もの領域があり、これらの領野はV1野、V2野を経て側頭連合野(temporal lobe)へと至る腹側経路(ventral pathway)と頭頂連合野(parietal lobe)へと至る背側経路(dorsal pathway)の2つの経路として構成されている。多くの領野では受容野構造の詳細はわかっていないが、細胞が伝達する視覚特徴については、適切な刺激セットを用いて細胞の応答に適切な刺激を同定するという方法で数多くの知見が得られている。これに基づき、腹側経路は物体の色、テクスチャーや形の分析に、背側経路は空間情報の伝達に関与していると考えられている。
細胞の受容野のサイズは高次の領域に向かうにつれて大きくなる。霊長類V1野で中心視野に受容野をもつ細胞の受容野は0.1~1度程度であるが、視覚経路の最終段階に位置するTE野では10度以上にもなる。ただし受容野サイズは偏心度にも依存し、中心視野では小さく、周辺視野ほど大きくなる。例えばV1野の周辺視野の受容野サイズは5度から10度程度である。またV1細胞の受容野位置は対側視野に限られるものが大部分であるが、視覚経路に沿って受容野サイズが大きくなるにつれて、同側視野も含むものが序々に増してくる。TE野ではほとんどの細胞が同側視野を受容野に含む。
受容野特性は、階層をあがるにつれて序次に複雑な刺激特徴を最適とするものが増してくる。たとえばV2野->V4野->TEO野->TE野と向かう腹側経路では、V2野に折れ線に反応する細胞、V4野にテクスチャーやパターンに反応する細胞、TEO野には物体の部分的特徴、TE野に至っては顔などの極めて複雑な特徴をもつ細胞が存在する。さらに、これらの細胞の多くは、受容野内部で刺激の位置、向き、あるいは形の手がかりを変えても特徴選択性を維持する。
体性感覚系の受容野
一次求心性神経繊維の受容野
触圧感覚をもたらす機械受容器には皮膚表面知覚に位置するマイスナー小体、メルケル終末と深部にあるパチニ小体、ルフィニ終末の4種類が知られている。マイスナー小体、メルケル終末につながる1次救心性繊維の受容野はスポット状で比較的小さく手では直径数ミリ程度である。パチニ小体、ルフィニ終末につながる繊維の受容野はそれよりも大きく、境界が不明瞭である場合が多い。有毛部には毛の動きを捉える毛包ユニットが知られているが、これらの1次繊維の受容野も四肢末端では直径数ミリ程度である温冷覚の1次繊維の受容野サイズも同定度である。痛覚繊維にも同程度の大きさをもつ比較的受容野の狭い特定的侵害受容ニューロンと、より受容野の大きい広作動閾ニューロンとがある。ただし、いずれの受容器の場合も、体幹に近いところでは受容野サイズは数十平方センチメートルと非常に大きくなる。
体性感覚野の受容野
1次体性感覚野は、視床からの入力が入る3a野、3b野と、そこから入力を受ける2野、1野に区分される。皮膚からの入力は3b野から主に1野へ、筋や腱からの入力は3a野から主に2野へと運ばれる。ただし1野、2野ともに3aおよび3bの両方から入力を受け取り、これらの入力は多くの細胞で収斂している。
各領野の細胞でみられる受容野サイズは1次繊維と比べるとはるかに大きく、手でも直径数センチメートルある。さらに3a野、3b野より1野や2野のほうが大きい。たとえば3b野の指に受容野をもつ細胞は指一本程度のものが多くあるが、1野や2野には数本の指に受容野が広がるものが数多くみられる。受容野は細胞が存在する大脳半球の反対側に限られる。
1野や2野の細胞は、3a野や3b野よりも複雑な受容野特性を示すことが知られており、たとえば表皮をこする物体の動きや、物体が伸びる向きや物体表面のテクスチャーなどに選択性を示す細胞が報告されている。
2次体性感覚野は1次体性感覚野から入力を受け取る。この領野の細胞は1次体性感覚野よりも広い受容野をもち、また体の両側の対称な場所に受容野をもつものが多い。たとえばある細胞は両手の5本指全体に受容野をもつ。さらに、これらの細胞は、皮膚だけでなく、いくつかの筋、腱からの入力が収斂しており、手全体や腕全体といった体の各パーツの姿勢の情報を伝達し、運動の感覚ガイダンスに関与していると考えられている。
- ↑ H. K. Hartline
The receptive fields of optic nerve fibers.
Am. J. Physiol: 1940. 130. 690-699. - ↑ 2.0 2.1
KUFFLER, S.W. (1953).
Discharge patterns and functional organization of mammalian retina. Journal of neurophysiology, 16(1), 37-68. [PubMed:13035466] [WorldCat] [DOI] - ↑
de Boer, R., & Kuyper, P. (1968).
Triggered correlation. IEEE transactions on bio-medical engineering, 15(3), 169-79. [PubMed:5667803] [WorldCat] [DOI] - ↑ 4.0 4.1
Jones, J.P., & Palmer, L.A. (1987).
The two-dimensional spatial structure of simple receptive fields in cat striate cortex. Journal of neurophysiology, 58(6), 1187-211. [PubMed:3437330] [WorldCat] [DOI] - ↑
DeAngelis, G.C., Ohzawa, I., & Freeman, R.D. (1993).
Spatiotemporal organization of simple-cell receptive fields in the cat's striate cortex. II. Linearity of temporal and spatial summation. Journal of neurophysiology, 69(4), 1118-35. [PubMed:8492152] [WorldCat] [DOI] - ↑
Rodieck, R.W. (1965).
Quantitative analysis of cat retinal ganglion cell response to visual stimuli. Vision research, 5(11), 583-601. [PubMed:5862581] [WorldCat] [DOI] - ↑
Enroth-Cugell, C., & Robson, J.G. (1966).
The contrast sensitivity of retinal ganglion cells of the cat. The Journal of physiology, 187(3), 517-52. [PubMed:16783910] [PMC] [WorldCat] [DOI] - ↑
Cleland, B.G., & Lee, B.B. (1985).
A comparison of visual responses of cat lateral geniculate nucleus neurones with those of ganglion cells afferent to them. The Journal of physiology, 369, 249-68. [PubMed:4093882] [PMC] [WorldCat] [DOI] - ↑
HUBEL, D.H., & WIESEL, T.N. (1959).
Receptive fields of single neurones in the cat's striate cortex. The Journal of physiology, 148, 574-91. [PubMed:14403679] [PMC] [WorldCat] [DOI] - ↑
Hubel, D.H., & Wiesel, T.N. (1968).
Receptive fields and functional architecture of monkey striate cortex. The Journal of physiology, 195(1), 215-43. [PubMed:4966457] [PMC] [WorldCat] [DOI] - ↑
Movshon, J.A., Thompson, I.D., & Tolhurst, D.J. (1978).
Spatial summation in the receptive fields of simple cells in the cat's striate cortex. The Journal of physiology, 283, 53-77. [PubMed:722589] [PMC] [WorldCat] [DOI] - ↑
Heeger, D.J. (1992).
Half-squaring in responses of cat striate cells. Visual neuroscience, 9(5), 427-43. [PubMed:1450099] [WorldCat] [DOI] - ↑ J. G. Daugman
Complete discrete 2-D Gabor transforms by neural networks for image analysis and compression.
IEEE Transactions on In Acoustics, Speech and Signal Processing: 1988, 36(7), 1169-1179. - ↑
Olshausen, B.A., & Field, D.J. (1996).
Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature, 381(6583), 607-9. [PubMed:8637596] [WorldCat] [DOI]