「マーの視覚計算理論」の版間の差分
細 →関連項目 |
細編集の要約なし |
||
| (同じ利用者による、間の5版が非表示) | |||
| 2行目: | 2行目: | ||
<font size="+1">[http://researchmap.jp/inui_toshio 乾 敏郎]</font><br> | <font size="+1">[http://researchmap.jp/inui_toshio 乾 敏郎]</font><br> | ||
''追手門学院大学''<br> | ''追手門学院大学''<br> | ||
DOI:<selfdoi /> | DOI:<selfdoi /> 原稿受付日:2021年6月19日 原稿完成日:2021年7月X日<br> | ||
担当編集委員:[https://researchmap.jp/kkitajo 北城 圭一](生理学研究所)<br> | 担当編集委員:[https://researchmap.jp/kkitajo 北城 圭一](生理学研究所)<br> | ||
</div> | </div> | ||
英:Marr’s computational theory of vision | 英:Marr’s computational theory of vision | ||
{{box|text= | {{box|text= Marrによると、情報処理装置は3つのレベルで理解する必要がある。それは、計算理論、情報表現とアルゴリズム、ハードウェア(実装)である。彼は視覚系を、初期視覚、中間視覚、高次視覚にわけ、それぞれについてこれら3つのレベルで独創的な研究を進めた。とくに、視覚計算理論の思想は、視覚系に限らず、広く脳科学や認知科学、心理学に大きな影響を与えた。}} | ||
== | ==Marrの視覚計算理論とは== | ||
David Marr (1945-1980)は、視覚研究において独創的な理論体糸を残し、一つの総合的アブローチを提唱した<ref name=ref1 /><ref>'''乾 敏郎 (1994).'''<br>視覚の計算理論.伊藤正男・安西祐一郎・川人光男・市川伸 一・中島秀之・橋田浩一(編)岩波講座「認知科学」第3巻『視覚と聴覚』''岩波書店'' 89-127</ref>。ここでは、一般の情報処理システムを理解するための3つのレベル、視覚情報処理を理解するための3つのレベルについて紹介した後、視覚情報処理の3段階について具体的に説明する。Marrの視覚研究の枠組みは当時としてはきわめて独創的なものであった。現在でも脳研究は3つのレベルでさまざまな検討がなされている<ref>'''Mather, G. (2015).'''<br>Computational approaches to perception: Beyond Marr’s (1982) computational approach to vision. In: Eysenck, M.W. and Groome, D. (Eds.) Cognitive psychology : Revisiting the classic studies, SAGE Publications, 38-46.<br>'''乾 敏郎 (訳, 2017)'''<br> 知覚の計算論的アプローチ- Marr(1982)による視覚の計算論的アプローチを超えて. 箱田 裕司, 行場 次朗(監訳)『古典で読み解く現代認知心理学』, ''北大路書房'', 49-60.</ref>。 | |||
==情報処理システムを理解するための3つのレベル== | ==情報処理システムを理解するための3つのレベル== | ||
Marrによると、情報処理装置は以下の3つのレベルで理解する必要がある。 | |||
すなわち、計算理論(computational theory)、入出力の情報表現と計算理論を実現するアルゴリズム(representation and algorithm)、ハードウェアもしくは神経回路という実装(implementation)のレベルである。 | すなわち、計算理論(computational theory)、入出力の情報表現と計算理論を実現するアルゴリズム(representation and algorithm)、ハードウェアもしくは神経回路という実装(implementation)のレベルである。 | ||
| 22行目: | 22行目: | ||
==視覚系を理解するための3つのレベル== | ==視覚系を理解するための3つのレベル== | ||
情報処理糸の研究をするためにはまずシステムの目的をはっきりさせねばならない。視覚系の目的はいろいろ考えられるが、Marr (1982)<ref name=ref1>'''Marr, D. (1982).'''<br>Vision: A computational investigation into the human representation and processing of visual information. New York, NY: W. H. Freeman & Company.<br>'''乾 敏郎,安藤広志(訳,1987)'''<br>『ビジョン-視覚の計算理論と脳内表現-』 産業図書.</ref> はまず網膜像の強度変化から実世界の3次元構造を推測することが視覚情報処理系の目的であると考えた。各過程はこの目的を遠成するために合理的に作られているはずである。そこでまずそれぞれの過程では何がどのような目的で計算されているのかを明らかにする必要がある。これが計算理論であり、システムの入出力の関係の記述と言える。 | |||
対象のさまざまな視覚属性は2次元網膜像から推定される。推定すべき属性の多くは、奥行きや3次元形状である。2次元データから3次元属性の推定は一般には解けない不良設定問題(ill-posed problem)である。ここで重要なことは、この計算が何らかの暗黙の仮定(制約条件)のもとでなされているということである。制約条件なしに計算しても解が一意に決まらないことが多い。しかし、我々は常に一つの知覚を経験している。これは何らかの制約条件が働いているからである。 | |||
つぎに計算理論が明らかになれば、計算がどのような手順(アルゴリズム)で実行されているのか、人出力はどのような表現形式が採用されているのかを明らかにせねばならない。 | つぎに計算理論が明らかになれば、計算がどのような手順(アルゴリズム)で実行されているのか、人出力はどのような表現形式が採用されているのかを明らかにせねばならない。 | ||
| 33行目: | 33行目: | ||
==視覚情報処理過程の3段階== | ==視覚情報処理過程の3段階== | ||
[[File:Inui_Marrs_computational_theory_of_vision_Fig.png|thumb|400px|'''図. | [[File:Inui_Marrs_computational_theory_of_vision_Fig.png|thumb|400px|'''図. Marrの視覚情報処理過程の枠組み''']] | ||
Marrは、視覚情報処理過程を大きく3段階に分けて議論した。すなわち、初期視覚(early vision)、中間視覚(middle vision)、高次視覚(high-level vision)である('''図''')。Marrの枠組みのなかで最大の特徴は、面の知覚が視覚系の最も重要な機能だとした点である。それまでの知覚観は線や図形といった2次元的な形態を捉えることを中心に議論されてきた。それに対して、Marrは外界の3次元構造を網膜像から推定することが視覚系の最大の特徴であると捉えたのである。ここにひとつの大きな転機が視覚心理学や生理学に訪れることとなった。 | |||
===初期視覚=== | ===初期視覚=== | ||
画像の強度を決定する要因として4つが挙げられる。(1)可視表面(visible surface)の幾何学的構造、(2)可視表面の反射率、(3)光景に対する照明、(4) | 画像の強度を決定する要因として4つが挙げられる。(1)可視表面(visible surface)の幾何学的構造、(2)可視表面の反射率、(3)光景に対する照明、(4)観察点である。画像は、これらすべての要因が混在している。初期視覚の目的は、どの強度変化がどの要因によるものかを種分けすることであり、4つの要因が分離された表現を作り出すことである。Marrは、2つの段階を経てこの目標が達成されていると考えた。すなわち、まず画像における変化と構造に関する適切な表現が得られる段階がある。ここには、強度変化の検出、局所的な幾何学的構造の表現と分析、光源や輝点および透過性といった照明効果の検出などが含まれる。この第1段階の結果得られる表現は原始スケッチ(primal sketch)と呼ばれた。 | ||
また初期視覚では明るさ、色、動き、陰影(shading and | また初期視覚では明るさ、色、動き、陰影(shading and shadow)、両眼視差、運動視差(motion parallax)、遮蔽輪郭(occluding contour)、テクスチャ(texture)などを原始スケッチに働くモジュールが多く存在すると考えられた。Marrは、これらのモジュールがすべて外界の構造推定のために情報を処理しているのだと考えた。 | ||
===中間視覚=== | ===中間視覚=== | ||
中間視覚においては、多くのモジュールの出力が統合されて可視表面の幾何学的構造の表現を作る。このレベルでは網膜中心座標系ではなく、観察者中心座標系で面の向きや奥行きが表現されると考え、その表現されたものを2.5次元スケッチと呼んだ。これは外界の構造推定ではあるが、観察者から見える面、すなわち可視表面に対する表現でしかないので、3次元の情報表現ではないという意味で酒落て付けられた名前である。観察者中心座標での表現なので頭を動かしても目を動かしても、安定して自分から面に対する向きや奥行きが表現されたものである。さらに2.5次元スケッチでは面の向きの不連続や奥行きの不連続が表現されたものであると捉えている。 | |||
===高次視覚=== | ===高次視覚=== | ||
最後の段階は、2. | 最後の段階は、2.5次元スケッチから観察者中心座標系ではなく物体中心座標系における物体の3次元表現である。最終段階である高次視覚ではパターン認識のための物体の表現が作られると考える。つまり物体に座標軸を持つ表現である。中心軸は細く伸びた方向など一般的なルールによって決められると考えられ、それに基づいて各部分間の関係などが記述され可視表面ではない裏の面(感覚可能物sensibilia)も表現されていると考えるのである。2.5次元スケッチは観察者を中心とした表現なので、観察者が移動して視点が変化することによってその表現は変化する。これまで見えていなかった面も見えるようになることもある。3次元表現は物体に座標軸を持つ表現であり、各視点からは見えない面も表現されているのである。したがって物体の位置や姿勢あるいは観察者の位置が変化しでもその表現は不変である。そして物体中心座標で表現された3次元表現は部分と全体が階層的に表された階層的表現であると考えた。 | ||
==参考文献== | ==参考文献== | ||
<references /> | <references /> | ||
2021年7月1日 (木) 17:21時点における版
英:Marr’s computational theory of vision
Marrによると、情報処理装置は3つのレベルで理解する必要がある。それは、計算理論、情報表現とアルゴリズム、ハードウェア(実装)である。彼は視覚系を、初期視覚、中間視覚、高次視覚にわけ、それぞれについてこれら3つのレベルで独創的な研究を進めた。とくに、視覚計算理論の思想は、視覚系に限らず、広く脳科学や認知科学、心理学に大きな影響を与えた。
Marrの視覚計算理論とは
David Marr (1945-1980)は、視覚研究において独創的な理論体糸を残し、一つの総合的アブローチを提唱した[1][2]。ここでは、一般の情報処理システムを理解するための3つのレベル、視覚情報処理を理解するための3つのレベルについて紹介した後、視覚情報処理の3段階について具体的に説明する。Marrの視覚研究の枠組みは当時としてはきわめて独創的なものであった。現在でも脳研究は3つのレベルでさまざまな検討がなされている[3]。
情報処理システムを理解するための3つのレベル
Marrによると、情報処理装置は以下の3つのレベルで理解する必要がある。
すなわち、計算理論(computational theory)、入出力の情報表現と計算理論を実現するアルゴリズム(representation and algorithm)、ハードウェアもしくは神経回路という実装(implementation)のレベルである。
この中で彼が最も重要であると考えたのは、計算理論のレベルである。計算理論は、ハードウェアとは独立にシステムの入出力関数を明らかにすることであると言える。システムがどのような計算を行っているのか、そして計算の目的は何かといったことを明らかにするのである。しかし計算理論が解ったからといってすべてが説明されたことにはならない。次のレベルでは計算理論を実現しているアルゴリズムとシステムの入力および出力の情報表現を明らかにしなければならない。これが明らかになった上でそのアルゴリズムがどのようなハードウェア(神経回路)によって実現されているかを説明する必要がある。
心理物理学は主に第2のレベル、神経生理学や解剖学は第3のレベルの研究に対応している。
視覚系を理解するための3つのレベル
情報処理糸の研究をするためにはまずシステムの目的をはっきりさせねばならない。視覚系の目的はいろいろ考えられるが、Marr (1982)[1] はまず網膜像の強度変化から実世界の3次元構造を推測することが視覚情報処理系の目的であると考えた。各過程はこの目的を遠成するために合理的に作られているはずである。そこでまずそれぞれの過程では何がどのような目的で計算されているのかを明らかにする必要がある。これが計算理論であり、システムの入出力の関係の記述と言える。
対象のさまざまな視覚属性は2次元網膜像から推定される。推定すべき属性の多くは、奥行きや3次元形状である。2次元データから3次元属性の推定は一般には解けない不良設定問題(ill-posed problem)である。ここで重要なことは、この計算が何らかの暗黙の仮定(制約条件)のもとでなされているということである。制約条件なしに計算しても解が一意に決まらないことが多い。しかし、我々は常に一つの知覚を経験している。これは何らかの制約条件が働いているからである。
つぎに計算理論が明らかになれば、計算がどのような手順(アルゴリズム)で実行されているのか、人出力はどのような表現形式が採用されているのかを明らかにせねばならない。
最後に、アルゴリズムがどのような神経回路で実現されているかが問題となる。
重要なことは、これらの水準の研究が一応独立して進められるのであるが、脳はこれらの計算が最適な構造で実行されているので、3つのレベルの研究はたがいに密接に関連しており、3つのレベルの研究を総合的に進める必要がある。
視覚情報処理過程の3段階
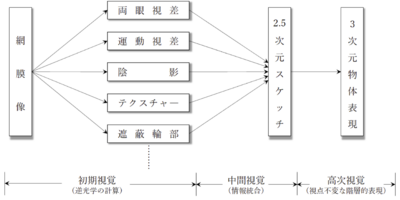
Marrは、視覚情報処理過程を大きく3段階に分けて議論した。すなわち、初期視覚(early vision)、中間視覚(middle vision)、高次視覚(high-level vision)である(図)。Marrの枠組みのなかで最大の特徴は、面の知覚が視覚系の最も重要な機能だとした点である。それまでの知覚観は線や図形といった2次元的な形態を捉えることを中心に議論されてきた。それに対して、Marrは外界の3次元構造を網膜像から推定することが視覚系の最大の特徴であると捉えたのである。ここにひとつの大きな転機が視覚心理学や生理学に訪れることとなった。
初期視覚
画像の強度を決定する要因として4つが挙げられる。(1)可視表面(visible surface)の幾何学的構造、(2)可視表面の反射率、(3)光景に対する照明、(4)観察点である。画像は、これらすべての要因が混在している。初期視覚の目的は、どの強度変化がどの要因によるものかを種分けすることであり、4つの要因が分離された表現を作り出すことである。Marrは、2つの段階を経てこの目標が達成されていると考えた。すなわち、まず画像における変化と構造に関する適切な表現が得られる段階がある。ここには、強度変化の検出、局所的な幾何学的構造の表現と分析、光源や輝点および透過性といった照明効果の検出などが含まれる。この第1段階の結果得られる表現は原始スケッチ(primal sketch)と呼ばれた。
また初期視覚では明るさ、色、動き、陰影(shading and shadow)、両眼視差、運動視差(motion parallax)、遮蔽輪郭(occluding contour)、テクスチャ(texture)などを原始スケッチに働くモジュールが多く存在すると考えられた。Marrは、これらのモジュールがすべて外界の構造推定のために情報を処理しているのだと考えた。
中間視覚
中間視覚においては、多くのモジュールの出力が統合されて可視表面の幾何学的構造の表現を作る。このレベルでは網膜中心座標系ではなく、観察者中心座標系で面の向きや奥行きが表現されると考え、その表現されたものを2.5次元スケッチと呼んだ。これは外界の構造推定ではあるが、観察者から見える面、すなわち可視表面に対する表現でしかないので、3次元の情報表現ではないという意味で酒落て付けられた名前である。観察者中心座標での表現なので頭を動かしても目を動かしても、安定して自分から面に対する向きや奥行きが表現されたものである。さらに2.5次元スケッチでは面の向きの不連続や奥行きの不連続が表現されたものであると捉えている。
高次視覚
最後の段階は、2.5次元スケッチから観察者中心座標系ではなく物体中心座標系における物体の3次元表現である。最終段階である高次視覚ではパターン認識のための物体の表現が作られると考える。つまり物体に座標軸を持つ表現である。中心軸は細く伸びた方向など一般的なルールによって決められると考えられ、それに基づいて各部分間の関係などが記述され可視表面ではない裏の面(感覚可能物sensibilia)も表現されていると考えるのである。2.5次元スケッチは観察者を中心とした表現なので、観察者が移動して視点が変化することによってその表現は変化する。これまで見えていなかった面も見えるようになることもある。3次元表現は物体に座標軸を持つ表現であり、各視点からは見えない面も表現されているのである。したがって物体の位置や姿勢あるいは観察者の位置が変化しでもその表現は不変である。そして物体中心座標で表現された3次元表現は部分と全体が階層的に表された階層的表現であると考えた。
参考文献
- ↑ 1.0 1.1 Marr, D. (1982).
Vision: A computational investigation into the human representation and processing of visual information. New York, NY: W. H. Freeman & Company.
乾 敏郎,安藤広志(訳,1987)
『ビジョン-視覚の計算理論と脳内表現-』 産業図書. - ↑ 乾 敏郎 (1994).
視覚の計算理論.伊藤正男・安西祐一郎・川人光男・市川伸 一・中島秀之・橋田浩一(編)岩波講座「認知科学」第3巻『視覚と聴覚』岩波書店 89-127 - ↑ Mather, G. (2015).
Computational approaches to perception: Beyond Marr’s (1982) computational approach to vision. In: Eysenck, M.W. and Groome, D. (Eds.) Cognitive psychology : Revisiting the classic studies, SAGE Publications, 38-46.
乾 敏郎 (訳, 2017)
知覚の計算論的アプローチ- Marr(1982)による視覚の計算論的アプローチを超えて. 箱田 裕司, 行場 次朗(監訳)『古典で読み解く現代認知心理学』, 北大路書房, 49-60.