「周波数地図」の版間の差分
細編集の要約なし |
細編集の要約なし |
||
| (同じ利用者による、間の2版が非表示) | |||
| 1行目: | 1行目: | ||
英語名 : tonotopy 独:Tonotopie 仏:tonotopie | 英語名 : tonotopy 独:Tonotopie 仏:tonotopie | ||
同義語:周波数局在、トノトピー | 同義語:周波数局在、トノトピー | ||
[[聴覚]]系の[[神経細胞]]は、特定の[[wikipedia:ja:周波数|周波数]]範囲の音に選択的に反応し、最も敏感に反応する周波数のことを特徴周波数と呼ぶ。周波数地図は、神経細胞がその特徴周波数の高低順に空間的に規則正しく配置されていることを指す。この構造は聴覚系の多くの部位で見られ、その成因は[[内耳]]に起源する。 | [[聴覚]]系の[[神経細胞]]は、特定の[[wikipedia:ja:周波数|周波数]]範囲の音に選択的に反応し、最も敏感に反応する周波数のことを特徴周波数と呼ぶ。周波数地図は、神経細胞がその特徴周波数の高低順に空間的に規則正しく配置されていることを指す。この構造は聴覚系の多くの部位で見られ、その成因は[[内耳]]に起源する。 | ||
== 定義 == | == 定義 == | ||
| 49行目: | 40行目: | ||
== 参考文献 == | == 参考文献 == | ||
<references /> | <references /> | ||
<br> (執筆者:宋文杰 担当編集委員:藤田一郎) | |||
2012年11月29日 (木) 11:24時点における版
英語名 : tonotopy 独:Tonotopie 仏:tonotopie
同義語:周波数局在、トノトピー
聴覚系の神経細胞は、特定の周波数範囲の音に選択的に反応し、最も敏感に反応する周波数のことを特徴周波数と呼ぶ。周波数地図は、神経細胞がその特徴周波数の高低順に空間的に規則正しく配置されていることを指す。この構造は聴覚系の多くの部位で見られ、その成因は内耳に起源する。
定義

右側のグラフは聴神経の周波数同調曲線の模式図。CF:特徴周波数。蝸牛底から蝸牛頂まで、CFが高低順に並んでいることを蝸牛の周波数地図と呼ぶ。
ある周波数の純音において、音圧を徐々に上昇させた時、細胞活動が初めて変化を示す音圧のことを閾値音圧と呼ぶ。周波数に従って閾値音圧が変化する様子を示す曲線は、その細胞の周波数同調曲線と呼ばれる(図1)。蝸牛神経から大脳皮質まで、多くの細胞の周波数同調曲線は左右非対称なV字型で、低い周波数側に伸びている。周波数同調曲線の最も低い部位が対応する周波数、即ち閾値音圧が最も低い周波数は、その細胞の特徴周波数と呼ばれる(図1)。周波数地図は神経細胞がその特徴周波数の高低順に空間的に規則正しく配置されていることを意味する。
聴覚路で見られる部位
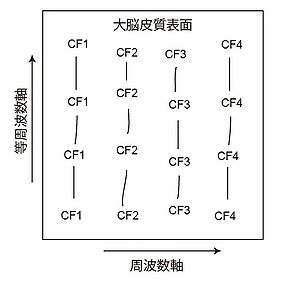
CF:特徴周波数。等しいCFを持つ細胞が並んでいる等周波数軸と、それに直交する周波数軸で、皮質表面の周波数地図が定義される。なお、深さ方向では、各層の細胞は大凡同じCFを持つ。
聴覚路において、周波数地図が内耳から大脳皮質聴覚野まで、すべてのレベルで見られる。内耳における蝸牛底から蝸牛頂までの周波数地図は一次元的で、cochleotopyとも呼ばれる。部位と特徴周波数の関係はGreenwoodの式で定量的に記述できる[1]。一方、大脳皮質では、皮質表面に垂直の方向から見れば、周波数地図は二次元的になっており、特徴周波数が徐々に変化する方向を周波数軸、それに垂直の方向では特徴周波数が変わらず、等周波数軸と呼ばれる[2] [3](図2)。皮質の深さ方向では、特徴周波数はほぼ一定である[3]。
起源
周波数地図の起源は内耳である。音刺激に対して蝸牛基底膜に、基底部から蝸牛孔に向かう進行波が生じ、その最大振幅が音の周波数に従って特定の部位で生じることで周波数地図が生まれる[4]。このことが生じる原因として、基底部から蝸牛孔に向かうに従って、基底膜の共振周波数が徐々に低くなることと、基底膜隣接部位間の機械的カップリングによるとされている[4]。また、外有毛細胞の電位依存性伸縮が基底膜の周波数同調曲線の先鋭化に非常に重要な働きをしており、その基盤にある電位感受性モータータンパク質のPrestinも同定されている[5] [6]。蝸牛以降の聴覚路において、周波数地図が保存されるのは、上位中枢への投射に常にトポグラフィーが存在するためである[7]。
機能
任意波形を周波数成分に分解するフーリエ変換が信号処理の分野で中心的な役割を果たすように、周波数地図は聴覚生理学における中心的な概念である。その存在は、聴覚系が音声情報を周波数帯域ごとに分解し、並列処理を行っていることを示している。周波数地図はピッチ受容や周波数弁別の神経基盤の一つを構成するのみならず、人工内耳の設計に重要な指針を与えている。一方、フーリエ変換の場合、逆変換で元の信号を復元できるが、周波数地図から神経活動のパタンを推定し、音声波形を正確に復元することは出来ない。事実、周波数地図から音刺激に対する神経活動のパタンを推定することすら困難である。その理由として、
- 特徴周波数は実験上定義されているもので、実際の音環境では音圧は閾値音圧より数十デシベルも高い。
- 音圧の変化に対する聴覚系の応答は非線形的である。音圧を固定して周波数ごとの反応を調べて、最も良く反応する周波数を最適周波数(Best frequency; BF)と呼ばれるが、BFは音圧に依存することが知られている[8]。
- 聴神経レベルでの2音抑圧[9]や中枢における2音抑制[10]など、周波数間の相互作用が見られる。
- 周波数に注目しているため、聴覚系反応の時間的な性質が無視されている。事実、特徴周波数依存的インパルス応答[11]、刺激音に対する位相同期(フェーズロック)[8]、時間ピッチなど、聴覚応答の時間的な側面が重要であることが知られている。
関連項目
参考文献
- ↑
Greenwood, D.D. (1990).
A cochlear frequency-position function for several species--29 years later. The Journal of the Acoustical Society of America, 87(6), 2592-605. [PubMed:2373794] [WorldCat] [DOI] - ↑
TUNTURI, A.R. (1952).
A difference in the representation of auditory signals for the left and right ears in the iso-frequency contours of the right middle ectosylvian auditory cortex of the dog. The American journal of physiology, 168(3), 712-27. [PubMed:14914884] [WorldCat] [DOI] - ↑ 3.0 3.1
Merzenich, M.M., Knight, P.L., & Roth, G.L. (1975).
Representation of cochlea within primary auditory cortex in the cat. Journal of neurophysiology, 38(2), 231-49. [PubMed:1092814] [WorldCat] [DOI] - ↑ 4.0 4.1 Békésy von G.
Experiments in hearing.
New York: McGraw Hill, 1960 - ↑
Dallos, P. (1992).
The active cochlea. The Journal of neuroscience : the official journal of the Society for Neuroscience, 12(12), 4575-85. [PubMed:1464757] [WorldCat] - ↑
Zheng, J., Shen, W., He, D.Z., Long, K.B., Madison, L.D., & Dallos, P. (2000).
Prestin is the motor protein of cochlear outer hair cells. Nature, 405(6783), 149-55. [PubMed:10821263] [WorldCat] [DOI] - ↑ Møller AR.
Hearing.
Amsterdam: Academic Press, 2006 - ↑ 8.0 8.1
Rose, J.E., Hind, J.E., Anderson, D.J., & Brugge, J.F. (1971).
Some effects of stimulus intensity on response of auditory nerve fibers in the squirrel monkey. Journal of neurophysiology, 34(4), 685-99. [PubMed:5000366] [WorldCat] [DOI] - ↑
Arthur, R.M., Pfeiffer, R.R., & Suga, N. (1971).
Properties of 'two-tone inhibition' in primary auditory neurones. The Journal of physiology, 212(3), 593-609. [PubMed:5557062] [PMC] [WorldCat] [DOI] - ↑
Spirou, G.A., Davis, K.A., Nelken, I., & Young, E.D. (1999).
Spectral integration by type II interneurons in dorsal cochlear nucleus. Journal of neurophysiology, 82(2), 648-63. [PubMed:10444663] [WorldCat] [DOI] - ↑
Carney, L.H., & Yin, T.C. (1988).
Temporal coding of resonances by low-frequency auditory nerve fibers: single-fiber responses and a population model. Journal of neurophysiology, 60(5), 1653-77. [PubMed:3199176] [WorldCat] [DOI]
(執筆者:宋文杰 担当編集委員:藤田一郎)